Окружность круг и их элементы часть 1 фипи ответы ширяева

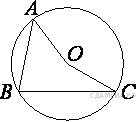
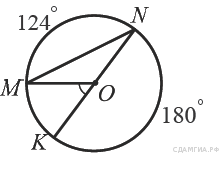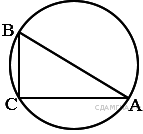В окружности с центром О проведены две хорды АВ и CD так, что центральные углы АОВ и СОD равны. На эти хорды опущены перпендикуляры ОК и OL. Докажите, что ОК и OL равны.

Треугольники АОВ и СОD равны по двум сторонам и углу между ними (AO = BO = CO = DO как радиусы окружности, ∠AOB = ∠COD по условию). Следовательно, высоты OK и OL равны как соответственные элементы равных треугольников.

Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.

Точка I равноудалена от A и B, поэтому она лежит на серединном перпендикуляре к отрезку AB. То же можно сказать и о J . Значит, IJ — серединный перпендикуляр к AB.

Задание 25 № 341422

Окружности с цен­тра­ми в точ­ках I и J пе­ре­се­ка­ют­ся в точ­ках A и B, причём точки I и J лежат по одну сто­ро­ну от пря­мой AB. Докажите, что от­рез­ки AB и IJ перпендикулярны.

Решение: IA и IB — радиусы окружности с центром в точке I => IA = IB => треугольник IAB — равнобедренный.

Проведем медиану IJ к стороне AB. Т.к. треугольник IAB — равнобедренный, то IJ также является высотой, проведённой AB => AB и IJ перпендикулярны, что и требовалось доказать.

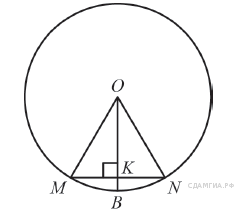
В окружности с центром O проведены две равные хорды и MN. На эти хорды опущены перпендикуляры OH и OS. Докажите, что OH и OS равны.

Проведем ОK, ON, OL, OM — радиусы. Треугольники KOL и MON равны по трем сторонам, тогда высоты OH и OS также равны как элементы равных треугольников. Что и требовалось доказать.

В окружности через середину O хорды AC проведена хорда BD так, что дуги AB и CD равны. Докажите, что O — середина хорды BD.

Вписанные углы ADB, CBD , ACB и DAC опираются на равные дуги, значит, они равны.

Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен AO:OC. Поскольку AO = OC , эти треугольники равны, следовательно, BO = OD.

Окружности с центрами в точках O₁ и O₂ не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n.

Проведём построения и введём обозначения, как показано на рисунке. Пусть Рассмотрим треугольники и они прямоугольные, углы и равны как вертикальные, следовательно, треугольники подобны, откуда

Видео:Урок 7. Окружность, круг и их элементы. ОГЭ. Вебинар |МатематикаСкачать

Материал для подготовки к ОГЭ по математике. Прототип задания №10 по теме: «Окружность, круг и их элементы»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Материал для подготовки к ОГЭ по математике

Прототип задания №10 по теме:

«Окружность, круг и их элементы»

1. Цен­траль­ный угол AOB опи­ра­ет­ся на хорду AB дли­ной 6. При этом угол OAB равен 60°. Най­ди­те ра­ди­ус окруж­но­сти.

2. В окруж­но­сти с цен­тром в точке O про­ве­де­ны диа­мет­ры AD и BC , угол OAB равен 70°. Най­ди­те ве­ли­чи­ну угла OCD .

3. В окруж­но­сти с цен­тром в точке О про­ве­де­ны диа­мет­ры AD и BC , угол OCD равен 30°. Най­ди­те ве­ли­чи­ну угла OAB .

4. Цен­траль­ный угол AOB , рав­ный 60°, опи­ра­ет­ся на хорду АВ дли­ной 3. Най­ди­те ра­ди­ус окруж­но­сти.

5. Най­ди­те гра­дус­ную меру ∠ MON , если из­вест­но, NP — диа­метр, а гра­дус­ная мера ∠ MNP равна 18°.

6. Най­ди­те ∠ DEF , если гра­дус­ные меры дуг DE и EF равны 150° и 68° со­от­вет­ствен­но.

7. Най­ди­те ∠ KOM , если гра­дус­ные меры дуг KO и OM равны 112° и 170° со­от­вет­ствен­но.

8. Най­ди­те гра­дус­ную меру ∠ ACB , если из­вест­но, что BC яв­ля­ет­ся диа­мет­ром окруж­но­сти, а гра­дус­ная мера ∠ AOC равна 96°.

9. Най­ди­те ∠ KOM , если из­вест­но, что гра­дус­ная мера дуги MN равна 124°, а гра­дус­ная мера дуги KN равна 180°.

10. В окруж­но­сти с цен­тром O AC и BD — диа­мет­ры. Цен­траль­ный угол AOD равен 112°. Най­ди­те впи­сан­ный угол ACB . Ответ дайте в гра­ду­сах.

11. В окруж­но­сти с цен­тром O AC и BD — диа­мет­ры. Угол ACB равен 26°. Най­ди­те угол AOD . Ответ дайте в гра­ду­сах.

12. Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC , если BD = 1 см, а ра­ди­ус окруж­но­сти равен 5 см.

13. Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду MN в её се­ре­ди­не — точке K . Най­ди­те длину хорды MN , если KB = 1 см, а ра­ди­ус окруж­но­сти равен 13 см.

14. Пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми 5 см и 12 см впи­сан в окруж­ность. Чему равен ра­ди­ус этой окруж­но­сти?

15. Точки A и B делят окруж­ность на две дуги, длины ко­то­рых от­но­сят­ся как 9:11. Най­ди­те ве­ли­чи­ну цен­траль­но­го угла, опи­ра­ю­ще­го­ся на мень­шую из дуг. Ответ дайте в гра­ду­сах.

16. Цен­траль­ный угол AOB равен 60°. Най­ди­те длину хорды AB , на ко­то­рую он опи­ра­ет­ся, если ра­ди­ус окруж­но­сти равен 5.

17. Най­ди­те ве­ли­чи­ну (в гра­ду­сах) впи­сан­но­го угла α , опи­ра­ю­ще­го­ся на хорду AB , рав­ную ра­ди­у­су окруж­но­сти.

18. В окруж­но­сти с цен­тром в точке O про­ве­де­ны диа­мет­ры AD и BC , угол OAB равен 25°. Най­ди­те ве­ли­чи­ну угла OCD .

19. В окруж­но­сти с цен­тром в точке O про­ве­де­ны диа­мет­ры AD и BC , угол OAB равен 70°. Най­ди­те ве­ли­чи­ну угла OCD .

20. В окруж­ность впи­сан рав­но­сто­рон­ний вось­ми­уголь­ник. Най­ди­те ве­ли­чи­ну угла ABC .

21. В окруж­ность впи­сан рав­но­сто­рон­ний вось­ми­уголь­ник. Най­ди­те ве­ли­чи­ну угла ABC .

22. В угол ве­ли­чи­ной 70° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся его сто­рон в точ­ках A и B . На одной из дуг этой окруж­но­сти вы­бра­ли точку C так, как по­ка­за­но на ри­сун­ке. Най­ди­те ве­ли­чи­ну угла ACB .

23. Ве­ли­чи­на цен­траль­но­го угла AOD равна 110°. Най­ди­те ве­ли­чи­ну впи­сан­но­го угла ACB . Ответ дайте в гра­ду­сах.

24. Точки A , B , C и D лежат на одной окруж­но­сти так, что хорды AB и СD вза­им­но пер­пен­ди­ку­ляр­ны, а ∠ BDC = 25°. Най­ди­те ве­ли­чи­ну угла ACD .

25. К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO . Най­ди­те ра­ди­ус окруж­но­сти, если AB = 12 см, AO = 13 см.

26. В тре­уголь­ни­ке ABC угол C равен 90°, AC = 20, tg A = 0,5. Най­ди­те BC .

27. В тре­уголь­ни­ке ABC угол C равен 90°, BC = 20, = 0,5. Най­ди­те AC .

28. В тре­уголь­ни­ке ABC угол C равен 90°, BC = 18, tg A = 3. Най­ди­те AC .

29. В тре­уголь­ни­ке ABC угол C равен 90°, AC = 30 , BC = Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

30. Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке O . Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC , если угол AOB равен 48°.

31. Цен­траль­ный угол AOB опи­ра­ет­ся на хорду АВ так, что угол ОАВ равен 60° . Най­ди­те длину хорды АВ , если ра­ди­ус окруж­но­сти равен 8.

32. Точка О — центр окруж­но­сти, ∠ AOB = 84° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла ACB (в гра­ду­сах).

33. В окруж­но­сти с цен­тром в точке O про­ве­де­ны диа­мет­ры AD и BC , угол OAB равен 70° . Най­ди­те ве­ли­чи­ну угла OCD .

34. Точка О — центр окруж­но­сти, ∠ ACB = 24° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла AOB (в гра­ду­сах).

35. Точка О — центр окруж­но­сти, ∠ BAC = 70° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла BOC (в гра­ду­сах).

36. Цен­траль­ный угол AOB , рав­ный 60° , опи­ра­ет­ся на хорду АВ дли­ной 4. Най­ди­те ра­ди­ус окруж­но­сти.

37. В тре­уголь­ни­ке ABC угол C равен 90° , BC = 20, tg A = 0,5. Най­ди­те AC .

38. В тре­уголь­ни­ке ABC угол C равен 90°, BC = 18, tg A = 3. Най­ди­те AC .

39. В тре­уголь­ни­ке ABC угол C равен 90°, AC = 12 , tg A = 1,5. Най­ди­те BC .

40. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 4. Угол при вер­ши­не, про­ти­во­ле­жа­щий ос­но­ва­нию, равен 120°. Най­ди­те диа­метр окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

41. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 5. Угол при вер­ши­не, про­ти­во­ле­жа­щий ос­но­ва­нию, равен 120°. Най­ди­те диа­метр окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 672 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Задание 16 ОГЭ 2023 математика | Окружность, круг и их элементыСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 539 513 материалов в базе

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 14.05.2016
• 5742
• 46

• 14.05.2016
• 2375
• 45

• 14.05.2016
• 2656
• 36

• 14.05.2016
• 1841
• 16

• 14.05.2016
• 903
• 6

• 14.05.2016
• 3059
• 15

• 14.05.2016
• 7329
• 37

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 14.05.2016 3048
• DOCX 358 кбайт
• 16 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Хохлова Наталья Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 3 месяца
• Подписчики: 1
• Всего просмотров: 391186
• Всего материалов: 99

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Задание 16 (часть 1) | ОГЭ 2024 Математика | Окружность, круг и их элементыСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Детский омбудсмен призвала предусматривать в школах условия для детей с инвалидностью

Время чтения: 3 минуты

Во Владивостоке средние классы школ переводят на дистанционное обучение

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

В Тульской области ввели школьные каникулы со 2 по 11 февраля

Время чтения: 1 минута

В России классы будут переводить на дистант, если заболели 20% детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Окружность. Круг. 5 класс.Скачать

Задания для подготовки к ОГЭ по теме «Окружность, круг и их элементы»

Задания для подготовки к ОГЭ по математике 9 класс модуль «Геометрия» по теме «Окружность, круг и их элементы», «Центральные и вписанные углы». Материалы составлены из заданий Образовательного портала для подготовки к экзаменам СДАМ ГИА Дмитрия Гущина.

Просмотр содержимого документа
«Задания для подготовки к ОГЭ по теме «Окружность, круг и их элементы»»

Задание №10. Окружность, круг и их элемены

Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 8

Длина хорды окружности равна 96, а расстояние от центра окруж­ности до этой хорды равно 20. Найдите диаметр окружности.

AC и BD — диаметры окружно­сти с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.

Найдите ∠KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°.

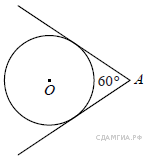
Из точки А проведены две каса­тельные к окружности с центром в точке О. Найдите радиус окруж­ности, если угол между касатель­ными равен 60°, а расстояние от точки А до точки О равно 8.

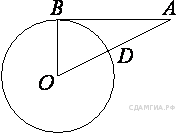
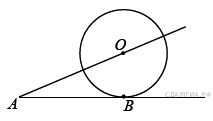
Отрезок AB = 40 касается окруж­ности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.

Точка О — центр окружности, ∠ACB = 24° . Найдите величину угла AOB (в градусах).

Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см

К окружности с центром в точке О проведены касатель­ная AB и секущая AO. Най­дите радиус окружности, если AB = 14 см, AO = 50 см.

В окружности с центром в точке O проведены диамет­ры AD и BC, угол OAB равен 25°. Найдите величи­ну угла OCD.

В окруж­но­сти с цен­тром O AC и BD — диа­мет­ры. Цен­траль­ный угол AOD равен 130°. Най­ди­те впи­сан­ный угол ACB. Ответ дайте в гра­ду­сах.

Сто­ро­на AC тре­уголь­ни­ка ABC про­хо­дит через центр опи­сан­ной около него окруж­но­сти. Най­ди­те ∠C , если ∠A = 44.

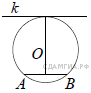
Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 85, длина хорды AB равна 102 (см. ри­су­нок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

На окруж­но­сти по раз­ные сто­ро­ны от диа­мет­ра AB взяты точки M и N. Из­вест­но, что ∠NBA = 38°. Най­ди­те угол NMB. Ответ дайте в гра­ду­сах.

Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 60°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

Вер­ши­ны тре­уголь­ни­ка делят опи­сан­ную около него окруж­ность на три дуги, длины ко­то­рых от­но­сят­ся как 3:4:11. Най­ди­те ра­ди­ус окруж­но­сти, если мень­шая из сто­рон равна 14.

К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окруж­но­сти, если AB = 12 см, AO = 13 см.

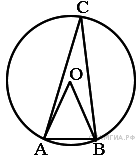
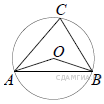
Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 48°.

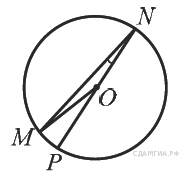
Най­ди­те гра­дус­ную меру ∠MON, если из­вест­но, NP — диа­метр, а гра­дус­ная мера ∠MNP равна 18°.

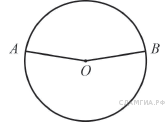
Точки A и B делят окруж­ность на две дуги, длины ко­то­рых от­но­сят­ся как 9:11. Най­ди­те ве­ли­чи­ну цен­траль­но­го угла, опи­ра­ю­ще­го­ся на мень­шую из дуг. Ответ дайте в гра­ду­сах.

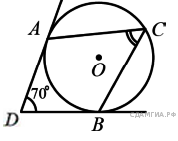
В угол ве­ли­чи­ной 70° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся его сто­рон в точ­ках A и B. На одной из дуг этой окруж­но­сти вы­бра­ли точку C так, как по­ка­за­но на ри­сун­ке. Най­ди­те ве­ли­чи­ну угла ACB.

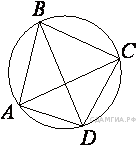
Че­ты­рех­уголь­ник ABCD впи­сан в окруж­ность. Угол ABC равен 70°, угол CAD равен 49°. Най­ди­те угол ABD. Ответ дайте в гра­ду­сах.

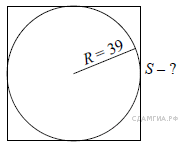
Окруж­ность впи­са­на в квад­рат. Най­ди­те пло­щадь квад­ра­та.

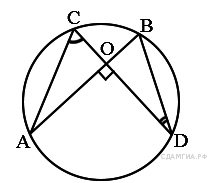
На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что 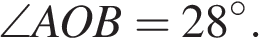Длина мень­шей дуги AB равна 63. Най­ди­те длину боль­шей дуги.

Точки A, B, C и D лежат на одной окруж­но­сти так, что хорды AB и СD вза­им­но пер­пен­ди­ку­ляр­ны, а ∠BDC = 25°. Най­ди­те ве­ли­чи­ну угла ACD.

Точка O – центр окруж­но­сти, на ко­то­рой лежат точки A, B и C. Из­вест­но, что ∠ABC = 15° и ∠OAB = 8°. Най­ди­те угол BCO. Ответ дайте в гра­ду­сах.

Ка­са­тель­ные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 24°. Най­ди­те угол ABO. Ответ дайте в гра­ду­сах.

Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду MN в её се­ре­ди­не — точке K. Най­ди­те длину хорды MN, если KB = 1 см, а ра­ди­ус окруж­но­сти равен 13 см.

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 30 , BC = 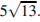Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 115°.

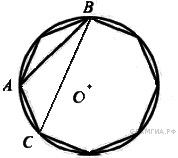
В окруж­ность впи­сан рав­но­сто­рон­ний вось­ми­уголь­ник. Най­ди­те ве­ли­чи­ну угла ABC.

В окруж­ность впи­сан рав­но­сто­рон­ний вось­ми­уголь­ник. Най­ди­те ве­ли­чи­ну угла ABC.

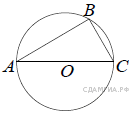
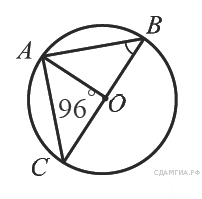
Най­ди­те гра­дус­ную меру ∠ACB, если из­вест­но, что BC яв­ля­ет­ся диа­мет­ром окруж­но­сти, а гра­дус­ная мера ∠AOC равна 96°.

В угол C ве­ли­чи­ной 79° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B. Най­ди­те угол AOB. Ответ дайте в гра­ду­сах.

📹 Видео

Задание 16 (часть 2) | ОГЭ 2024 Математика | Окружность, круг и их элементыСкачать

Задание 16.Окружность, круг и их элементы. Часть 1Скачать

Окружность, круг и их элементы. A circle, and their elements.Скачать

ЕГЭ. Математика. Окружность, круг и их элементы. ПрактикаСкачать

ОГЭ по математике: окружность, круг и их элементы (Задание №17)Скачать

Математика. 3 класс. Окружность, круг и их элементы /24.11.2020/Скачать

Геометрия. 7 класс. Окружность, круг, их элементы и части /01.04.2021/Скачать

ОГЭ по математике 2019. Задание 17. Окружность, круг и их элементы. Теория+задачи (часть 1)Скачать

Задание 6. Часть 3. Окружность, круг и их элементыСкачать

Окружность и круг | Часть 1 | основные понятия и элементыСкачать

Задание 16 (часть 3) | ОГЭ 2024 Математика | Окружность, круг и их элементыСкачать

17 задание ОГЭ. 17.1.2. Окружность, круг и их элементыСкачать

Окружность. Круг. Практическая часть - решение задачи. 5 класс.Скачать

ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

17 задание ОГЭ. 17.1.3. Окружность, круг и их элементыСкачать