Окружность проходит через вершину С прямоугольника ABCD, касается стороны AB, пересекает сторону CD в точке M и касается стороны AD в точке K.
А) Докажите, что угол CKD равен углу KMD.
Б) Найдите сторону AB, зная, что AD = 18, DM = 4.
А) Угол KCD — вписанный в заданную окружность, значит, измеряется половиной градусной меры дуги KM. А угол MKD образован хордой KM этой же окружности и касательной KD к той же окружности, и он измеряется половиной градусной меры дуги KM, заключенной между хордой и касательной. Значит, ∠KCD = ∠MKD. Но эти два угла есть острые углы двух прямоугольных треугольников KCD и MKD. Тогда обязаны быть равными и другие острые углы названных треугольников, т. е. ∠CKD = ∠KMD, что и требовалась доказать.
Б) Из полученного равенства ∠CKD = ∠KMD следует подобие: ΔMKD
Пусть R — радиус заданной окружности, O — ее центр, F ∈ CM, OF ⊥ CM. Пусть E ∈ AB, OE ⊥ AB.
Соединим точки O и K, O и E отрезками , тогда OK = OE = R. Кроме того, OK ⊥ KD. OE || AK как два перпендикуляра к AB. По аналогичной причине Следовательно, AEOK — параллелограмм, откуда AE = OK = R. Но AE = AK как отрезки касательных к окружности, проведенных из точки А. Следовательно, AK = AE = R. В таком случае KD = 18 − R.
Рассмотрим OE и OF как два перпендикуляра, проведенные из одной и той же точки О к параллельным прямым AB и CD, лежат на одной прямой. Тогда AEFD — прямоугольник, откуда: FD = AE = R.
Пусть CD = x, тогда CM = CD − MD = x − 4.
Треугольник COM — равнобедренный, в нем OF — высота по построению, следовательно, OF — медиана.
Это — с одной стороны. С другой же стороны, CF = CD − FD = x − R. Значит,
Так как KD = 18 − R, то в соответствии с равенствами (*) и (**) будем иметь:
Значение R = 34 не подходит по смыслу задачи, так как KD = 18 − R > 0.
При R = 10: AB = CD = x = 2R − 4 = 20 − 4 = 16.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
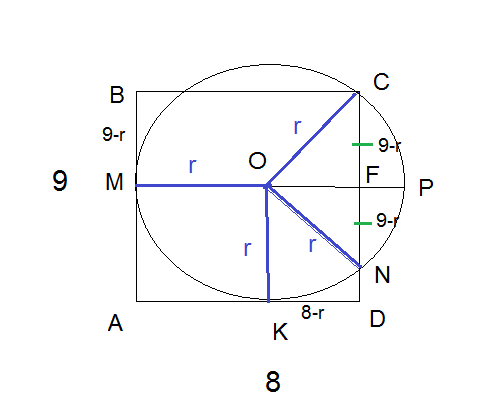
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Содержание Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Задача 28899 6. Дан прямоугольник ABCD со сторонами.Условие6. Дан прямоугольник ABCD со сторонами АВ = 9 см и AD = 8 см. Окружность касается сторон АВ и AD прямоугольника ABCD, проходит через вершину С и пересекает сторону DC в точке N. Найдите площадь трапеции ABND. РешениеКасательная перпендикулярна радиусу, проведенному в точку касания. Треугольник СON — равнобедренный ( OC=ON=r) r^2-34r+145=0 S ( трапеции ABND)=(AB+ND)*AD/2=(9+1)*8/2=40 О т в е т. 40 кв см. Видео:Геометрия Окружность касается большего катета прямоугольного треугольника, проходит через вершинуСкачать  Окружность касается сторон прямоугольника и проходит через вершинуБАЗА ЗАДАНИЙ Задание № 16. Планиметрия с доказательством. 1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D. 2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. 3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD. 4. В треугольнике ABC точки A 1 , B 1 , C 1 — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°. 5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно. 6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P. 7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L. 8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N. 9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D. 10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны. 11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно. 12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB. 13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый. 14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C 1 , B 1 соответственно. 15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD. 16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота. 17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M. 18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно. 19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно. б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60. 20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD. 21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K. 22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L 23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части. 24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P. 25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K. 26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности. 27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O. 28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17. 🎦 ВидеоОкружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать 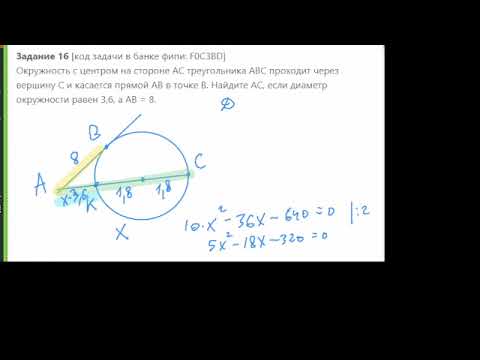 Окружность касается сторон параллелограмма и биссектрисы.Скачать  ОКРУЖНОСТЬ и ПРЯМОУГОЛЬНИК. ГЕНИАЛЬНО!Скачать  Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать  Окружность касается! И ВСЕХ КАСАЕТСЯ!Скачать  В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Геометрия Окружность центр которой принадлежит гипотенузе прямоугольного треугольника касаетсяСкачать  Задание 24 ОГЭ по математике #3Скачать  ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать  ОГЭ. Задание 24. Геометрическая задача на вычислениеСкачать  🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать  ВПИСАННАЯ ОКРУЖНОСТЬ + ПРАВИЛА ОФОРМЛЕНИЯ!Скачать  ЗАДАЧА - ПРОСТО ОТДЫХ КАКОЙ-ТО!Скачать  Окружность проходит через вершины А, В и D параллелограммаСкачать  ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать  Геометрия. ОГЭ по математике 2021. Вебинар | МатематикаСкачать  ОГЭ без рекламы математика задача 25 7 и 8 вариантСкачать  |