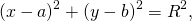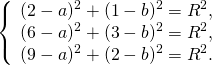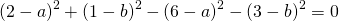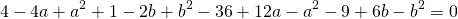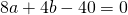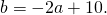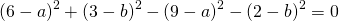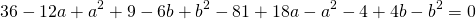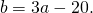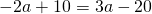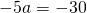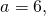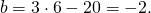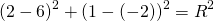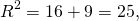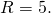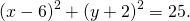Окружность проходит через вершины B и C треугольника ABC и пересекает AB и AC в точках C1 и B1 соответственно.
а) Докажите, что треугольник ABC подобен треугольнику AB1C1.
б) Найдите радиус данной окружности, если ∠A = 45°, B1C1 = 6 и площадь треугольника AB1C1 в восемь раз меньше площади четырёхугольника BCB1C1.
Четырёхугольник BCB1C1 вписан в окружность, поэтому
Следовательно, треугольники ABC и AB1C1 подобны по двум углам.
б) Площадь треугольника AB1C1 в восемь раз меньше площади четырёхугольника BCB1C1, поэтому площадь треугольника ABC в девять раз больше площади треугольника AB1C1 и коэффициент подобия этих треугольников равен 3. Пусть тогда
Найдём BB1 по теореме косинусов:
Теперь по теореме синусов из треугольника ABB1 получаем:
Но поскольку синусы смежных углов равны. Получаем
Теперь находим радиус окружности, описанной около треугольника BB1C:
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание
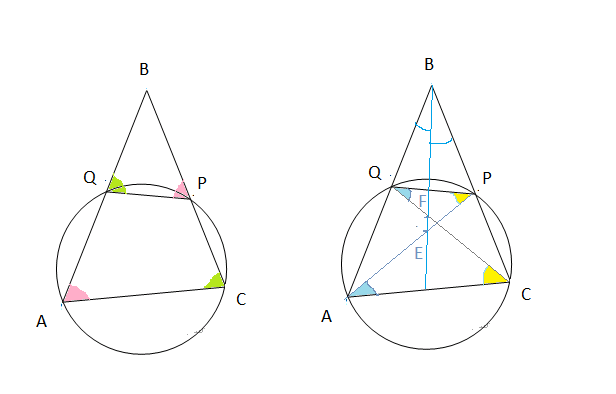
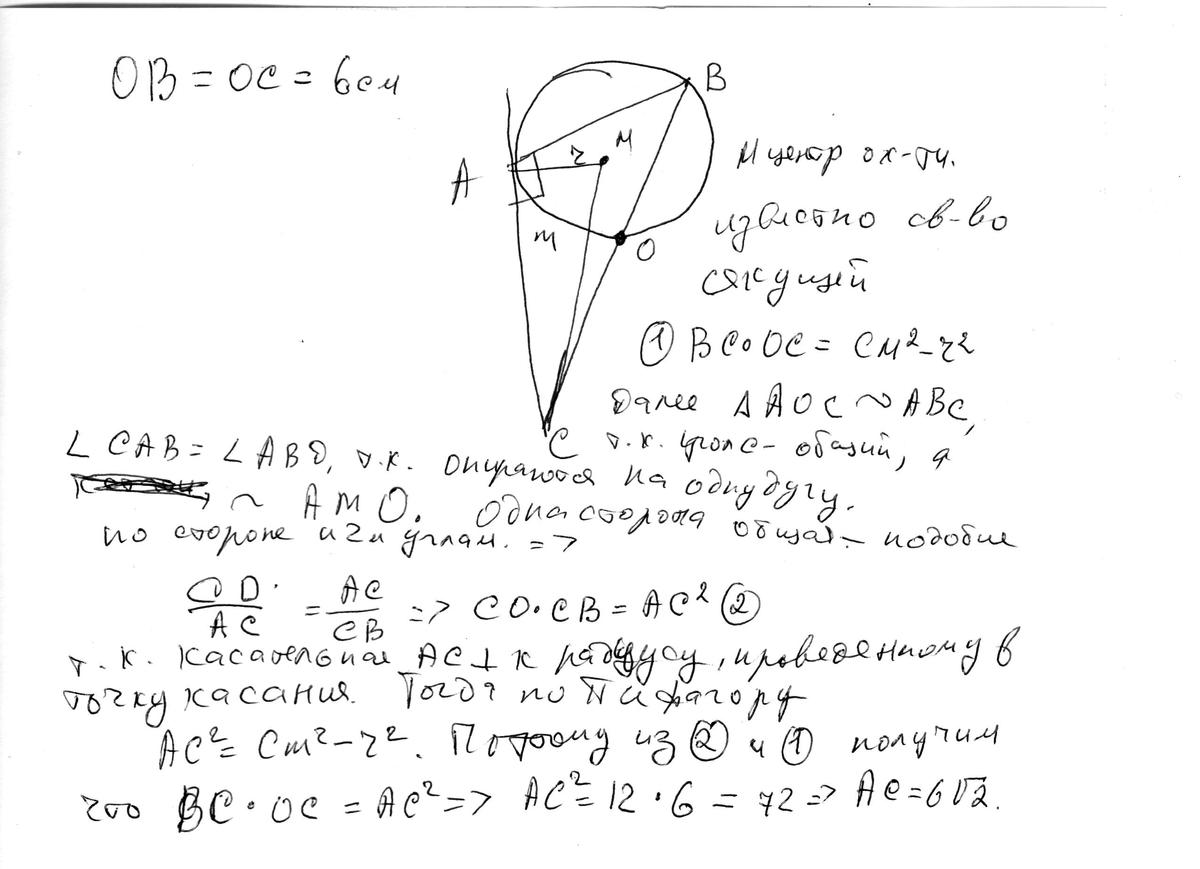
Видео:Геометрия Вершины треугольника делят описанную около него окружность на три дуги, длины которыхСкачать  Уравнение описанной окружностиКак составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника? Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности. Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2). Подставив координаты вершин треугольника в уравнение окружности получим систему уравнений Вычтем из первого уравнения системы второе: Теперь из второго уравнения системы вычтем третье: Приравняем правые части равенств b=-2a+10 и b=3a-20: Подставим в первое уравнение системы a=6 и b=-2: a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин. Видео:Вершины треугольника делят окружность на три дуги, длины которых относятся как 3:4:11Скачать  Окружность проходит через вершины а и с в треугольникеВидео:Окружность вписанная в треугольник и описанная около треугольника.Скачать  Задача 21138 Окружность, проходящая через вершины А и.УсловиеОкружность, проходящая через вершины А и С треугольника АВС, пересекает стороны AB и CB в точках Q и P соответственно. Биссектриса угла ABC пересекает отрезок AP в точке E и отрезок CQ – в точке F. Найдите длину AE, если QF=6, PE=7, CF=9. РешениеЧетырехугольник AQPC вписан в окружность, суммы противолежащих углов равны 180 градусов. Треугольник АВС и AQP подобны по двум углам. Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника AE:EP=FC:QF Видео:Вершины треугольника делят окружность на три дуги, длины которых относятся как 6:13:17Скачать  Окружность проходит через вершины А и В треугольника АВС, касается стороны АС в точке А и пересекает сторону ВС в ее середине — точке О?Геометрия | 10 — 11 классы Окружность проходит через вершины А и В треугольника АВС, касается стороны АС в точке А и пересекает сторону ВС в ее середине — точке О. Вычислите длину стороны АС, если известно, что ОВ = 6см. Решение в скане. Видео:№581. Вершины треугольника ABC лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы доСкачать 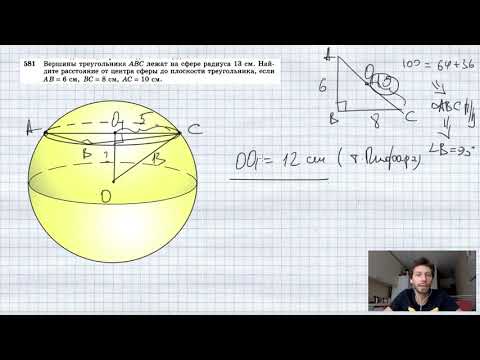 В треугольнике АВС известны стороны : АВ = 7, ВС = 10, АС = 8?В треугольнике АВС известны стороны : АВ = 7, ВС = 10, АС = 8. Окружность, проходящая Через точки А и С, пересекает прямые ВА и ВС соответственно в точках К и Л, отличных от вершин треугольника. Отрезок КЛ касается окружности, вписанной в треугольник АВС. Найдите длину отрезка КЛ. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В?Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдит5е АС, если диаметр окружности равен 15, а АВ = 4. Видео:Геометрия. 7 класс. Урок 9 "Окружность проходящая через вершины треугольника"Скачать  В треугольнике авс на стороне ас как на диаметре построена окружность ?В треугольнике авс на стороне ас как на диаметре построена окружность . Эта окружность проходит через середину стороны вс и пересекается в точке д продолжение стороны ав за точку а , причем ад = 0, 25 ас . Найдите площадь треугольника авс если ав = 1. Видео:Изогонали угла. Радиус описанной окружности и высота, проведенные из одной вершины треугольника.Скачать  В треугольнике АВС со сторонами АВ = 7см, ВС = 9см, АС = 10см вписана окружность, касающаяся стороны АС в точке Е?В треугольнике АВС со сторонами АВ = 7см, ВС = 9см, АС = 10см вписана окружность, касающаяся стороны АС в точке Е. Найдитерасстояние от точки Е до точки К биссектрисы ВК. Видео:ЕГЭ Математика Задание 6#27935Скачать  В треугольнике АВС известны длины сторон АВ = 14 , АС = 98, точка О — центр окружности , описанной около треугольника АВС ?В треугольнике АВС известны длины сторон АВ = 14 , АС = 98, точка О — центр окружности , описанной около треугольника АВС . Прямая ВD, перпендикулярная прямой АО пересекает сторону АС и точке D. Видео:Геометрия Вершины треугольника соединены с центром вписанной в него окружности Проведенные отрезкиСкачать  . Окружность, проходящая через вершины А и В треугольника АВС, пересекает стороны АС и ВС в точках L и K соответственно?. Окружность, проходящая через вершины А и В треугольника АВС, пересекает стороны АС и ВС в точках L и K соответственно. Докажите, что треугольники АВС и CKL подобны. Видео:Геометрия Вершины равнобедренного треугольника ABC (AB = BC) делят описанную около него окружностьСкачать  Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В?Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности, если АВ = 2, АС = 8. Видео:8 Расстояние от вершины треугольника до точек касания вписанной окружности со сторонамиСкачать  В треугольнике АВС известны длины сторон АВ = 32 АС = 64, точка О — центр окружности, описанной около треугольника АВС?В треугольнике АВС известны длины сторон АВ = 32 АС = 64, точка О — центр окружности, описанной около треугольника АВС. Прямая ВД, перпендикулярная прямой АО, пересекает сторону АС в точке Д. Видео:✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать  Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В?Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 5, 25, а АВ = 9. Видео:Три точки, задающие окружностьСкачать  В треугольнике АВС известны длины сторон АВ = 8 и АС = 64?В треугольнике АВС известны длины сторон АВ = 8 и АС = 64. Точка О центр окружности, описанной около треугольника АВС. Прямая ВD перпендикулярная прямой АО , пересекает сторону АС в точке D. На этой странице находится вопрос Окружность проходит через вершины А и В треугольника АВС, касается стороны АС в точке А и пересекает сторону ВС в ее середине — точке О?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку. Как — то так, а четвертое, незнаю. Во — первых, геометрия знакомит нас с окружающей действительностью, в которой многие предметы напоминают различные геометрические фигуры, фактически мы живем в мире геометрии. Во — вторых в равной степени геометрия нужна и математику, и инженеру, и .. 1. Фронтально — проецирующая плоскость 2. Горизонтально — проецирующая плоскость 3. Профильно — проецирующая плоскость 4. Фронтальная плоскость уровня 5. Горизонтальная плоскость уровня 6. Профильная плоскость уровня. Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Задание №188Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать  УсловиеВ треугольнике ABC окружность проходит через точки B и C и пересекает стороны AB и AC в точках M и N соответственно. Отрезок MN касается окружности, вписанной в треугольник ABC . а) Докажите, что bigtriangleup ABC подобен bigtriangleup ANM . б) Найдите MN , если AB=7, AC=8, BC=9 . Видео:Геометрия Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВССкачать  Решениеа) Окружность с центром в точке O_1 описана около четырехугольника BMNC , значит, angle BCN+angle BMN =180^ , angle BMN=180^ -angle BCN . angle AMN+angle BMN=180^ , как смежные, angle BMN=180^ -angle AMN. Отсюда angle BCN=angle AMN . Имеем в треугольниках ABC и ANM : angle A — общий, angle ACB=angle NCB=angle AMN, значит, bigtriangleup ABC подобен bigtriangleup ANM по первому признаку подобия, что требовалось доказать. Окружность с центром в точке O вписана в bigtriangleup ABC, значит AF=AE, BE=BP, CP=CF , как отрезки касательных, проведенных к окружности c центром O_1 из точек A, B и C соответственно. Пусть AF=AE=x, тогда BE=BP=7-x, CP=CF=8-x, BP+CP=BC, 7-x+8-x=9, x=3, AF=AE=3 . Обозначим MK=t, NK=p, тогда ME=MK=t, NF=NK=p как отрезки касательных, проведенных к окружности с центром O из точек M и N соответственно. Получим AM=AE-ME=3-t, AN=AF-NF=3-p, MN=MK+NK=t+p . Периметр bigtriangleup AMN равен AM+AN+MN=3-t+3-p+t+p=6. Периметры подобных треугольников относятся так же как и их стороны, поэтому frac =frac , MN=frac =2,25 📸 ВидеоРазбор Задачи №16 из работы Статград от 29 января 2020 (Запад)Скачать  №665. Вершины треугольника ABC лежат на окружности. Докажите, что если АВ — диаметр окружностиСкачать  Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать  |