Около любого правильного многоугольника можно описать окружность

Теорема

Доказательство

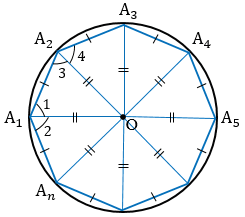
Дано: А₁А₂А₃. А_n — правильный многоугольник.

Доказательство:

Пусть точка О — точка пересечения биссектрис углов А₁ и А₂. Соединим точку О отрезками с остальными вершинами многоугольника и докажем, что ОА₁ = ОА₂ = . = ОА_n.

А₁А₂А₃. А_n — правильный многоугольник, значит, А₁ = А₂, тогда 1 = 3 (т.к. ОА₁ и ОА₂ биссектрисы равных углов А₁ и А₂), следовательно,

А₁ОА₂ — равнобедренный (по признаку равнобедренного треугольника), поэтому ОА₁ = ОА₂.

А₁ОА₂ = А₂ОА₃ по двум сторонам и углу между ними (А₁А₂ = А₂А₃ как стороны правильного многоугольника, ОА₂ — общая, 3 = 4, т.к. ОА₂ биссектриса угла А₂), следовательно,

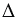
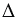
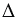
ОА₁ = ОА₃. Аналогично можно доказать, что ОА₂ = ОА₄, ОА₃ = ОА₅ и т.д.

Итак, ОА₁ = ОА₂ = . = ОА_n, значит, точка О равноудалена от всех вершин многоугольника. Поэтому окружность с центром О и радиусом ОА₁ является описанной около многоугольника А₁А₂А₃. А_n.

Докажем, что описать можно только одну окружность.

Рассмотрим какие-нибудь три вершины многоугольника А₁А₂А₃. А_n, например, А₁, А₂, А₃. Мы можем начертить только одну окружность одновременно проходящую через три точки А₁, А₂, А₃ (смотри доказательство), т.е. другой окружности проходящей через три данные точки не существует, значит, около многоугольника А₁А₂А₃. А_n можно описать только одну окружность, т.к. точки А₁, А₂, А₃ — вершины данного многоугольника. Теорема доказана.

Поделись с друзьями в социальных сетях:

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Около любого правильного многоугольника можно описать окружность

Какие из следующих утверждений верны?

1) Около любого правильного многоугольника можно описать не более одной окружности.

2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

4) Около любого ромба можно описать окружность.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Около любого правильного многоугольника можно описать не более одной окружности.»— верно, около любого правильного многоугольника можно описать окружность, и притом только одну.

2) «Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.» — верно, треугольник с такими сторонами является прямоугольным, таким образом, центр окружности лежит на гипотенузе.

3) «Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.» — верно, диагонали квадрата точкой пересечения делятся пополам, таким образом, центром окружности является точка пресечения диагоналей.

4) «Около любого ромба можно описать окружность.» — неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

Около любого многоугольника можно описать окружность

Видео:Окружность, описанная около правильного многоугольника | Геометрия 7-9 класс #105 | ИнфоурокСкачать

Окружность, описанная около правильного многоугольника

Теорема

Доказательство

Дано: А₁А₂А₃. А_n — правильный многоугольник.

Доказательство:

Пусть точка О — точка пересечения биссектрис углов А₁ и А₂. Соединим точку О отрезками с остальными вершинами многоугольника и докажем, что ОА₁ = ОА₂ = . = ОА_n.

А₁А₂А₃. А_n — правильный многоугольник, значит, А₁ = А₂, тогда 1 = 3 (т.к. ОА₁ и ОА₂ биссектрисы равных углов А₁ и А₂), следовательно,

А₁ОА₂ — равнобедренный (по признаку равнобедренного треугольника), поэтому ОА₁ = ОА₂.

А₁ОА₂ = А₂ОА₃ по двум сторонам и углу между ними (А₁А₂ = А₂А₃ как стороны правильного многоугольника, ОА₂ — общая, 3 = 4, т.к. ОА₂ биссектриса угла А₂), следовательно,

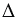
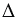
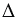
ОА₁ = ОА₃. Аналогично можно доказать, что ОА₂ = ОА₄, ОА₃ = ОА₅ и т.д.

Итак, ОА₁ = ОА₂ = . = ОА_n, значит, точка О равноудалена от всех вершин многоугольника. Поэтому окружность с центром О и радиусом ОА₁ является описанной около многоугольника А₁А₂А₃. А_n.

Докажем, что описать можно только одну окружность.

Рассмотрим какие-нибудь три вершины многоугольника А₁А₂А₃. А_n, например, А₁, А₂, А₃. Мы можем начертить только одну окружность одновременно проходящую через три точки А₁, А₂, А₃ (смотри доказательство), т.е. другой окружности проходящей через три данные точки не существует, значит, около многоугольника А₁А₂А₃. А_n можно описать только одну окружность, т.к. точки А₁, А₂, А₃ — вершины данного многоугольника. Теорема доказана.

Поделись с друзьями в социальных сетях:

Видео:Правильный многоугольник. Окружность, описанная около правильного многоугольника.Скачать

Около любого многоугольника можно описать окружность

Какие из следующих утверждений верны?

1) Около любого правильного многоугольника можно описать не более одной окружности.

2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

4) Около любого ромба можно описать окружность.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Около любого правильного многоугольника можно описать не более одной окружности.»— верно, около любого правильного многоугольника можно описать окружность, и притом только одну.

2) «Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.» — верно, треугольник с такими сторонами является прямоугольным, таким образом, центр окружности лежит на гипотенузе.

3) «Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.» — верно, диагонали квадрата точкой пересечения делятся пополам, таким образом, центром окружности является точка пресечения диагоналей.

4) «Около любого ромба можно описать окружность.» — неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Описанная окружность

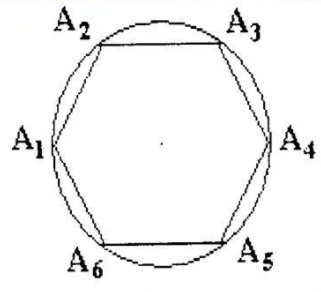
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанная окружность

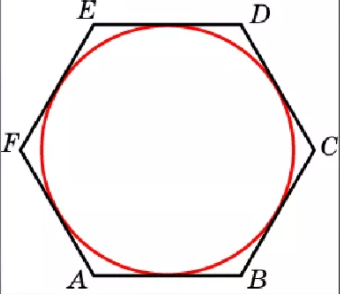
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 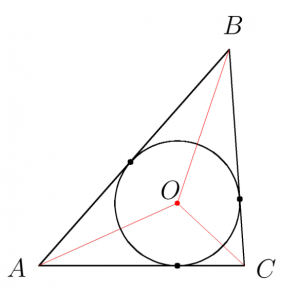Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

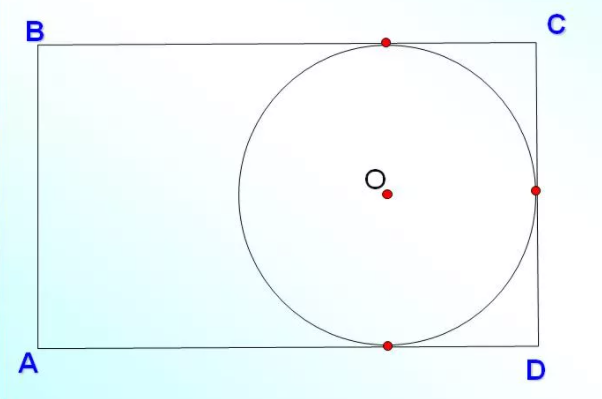
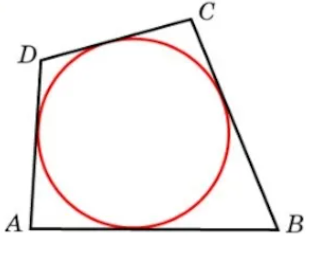
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

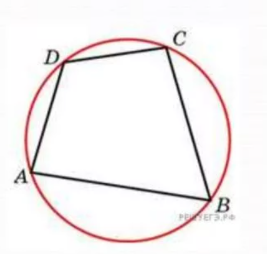
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

🔥 Видео

Правильные многоугольники. Урок 11. Геометрия 9 классСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Окружность, вписанная в правильный многоугольник | Геометрия 7-9 класс #106 | ИнфоурокСкачать

Большие последствия мелких расходов: ФАКТОР ЛАТТЕ. МИЛЛИОНЕР – АВТОМАТИЧЕСКИ // Дэвид БахСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

111. Окружность, вписанная в правильный многоугольникСкачать

ОПИСАННАЯ ОКРУЖНОСТЬ около многоугольника | геометрия 9 классСкачать