Одномерный вектор что это (8 видео) | Курс школьной геометрии

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Содержание

Линейная алгебра
Что такое вектор
Как записывать
Скаляр
Как изображать
И зачем нам это всё
Что дальше
n-мерные векторы, операции над ними.
Векторы в C++: для начинающих
Что такое вектор (vector)
Как создать вектор (vector) в C++
Второй способ обратиться к ячейке
Как указать количество ячеек для вектора
Как сравнить два вектора
📹 Видео

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Что такое массив. Примеры. Теория. Array. Одномерный массив. Синтаксис. C++. Урок #25.Скачать

Что такое вектор

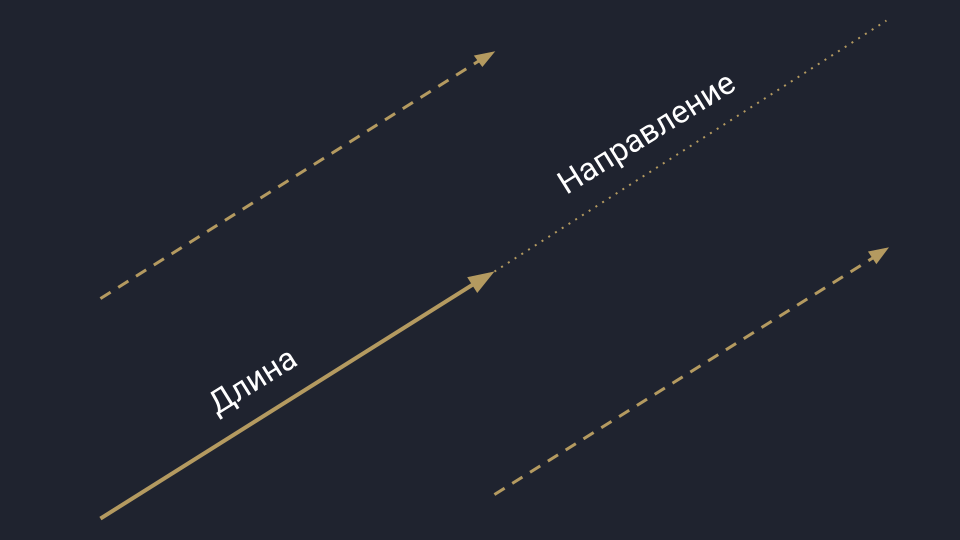
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

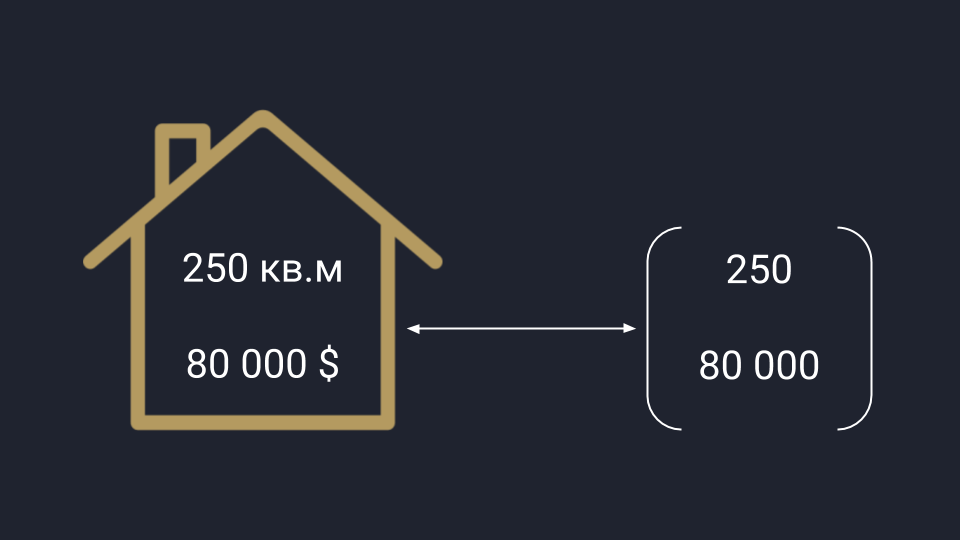
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

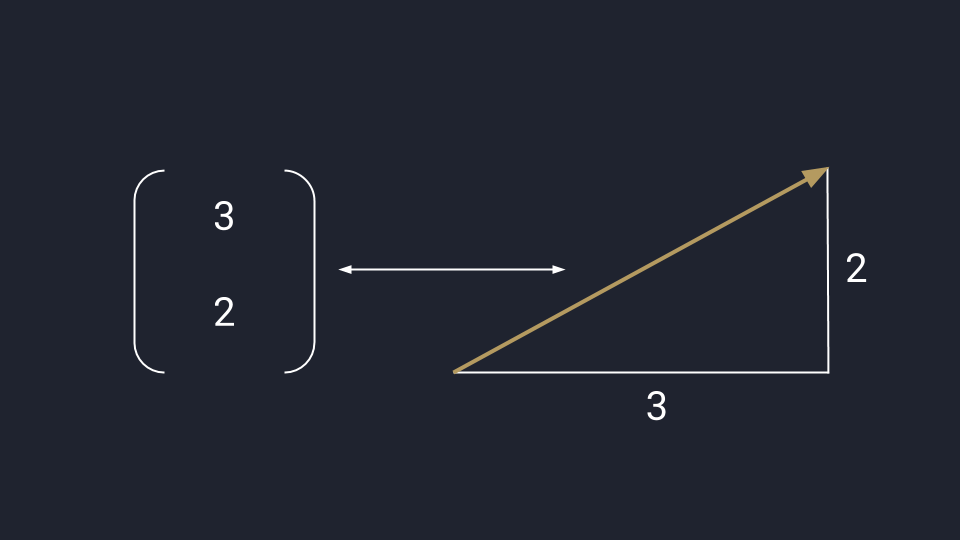
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

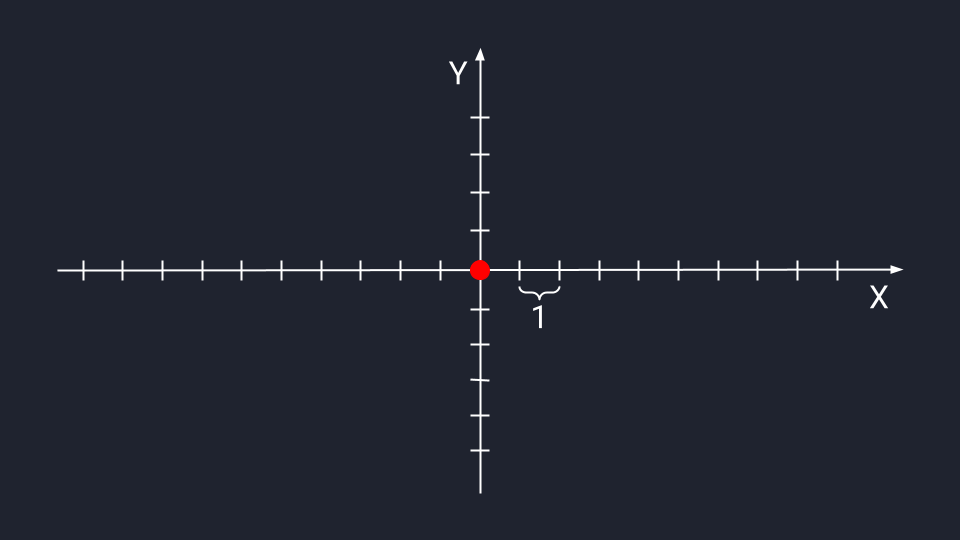
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

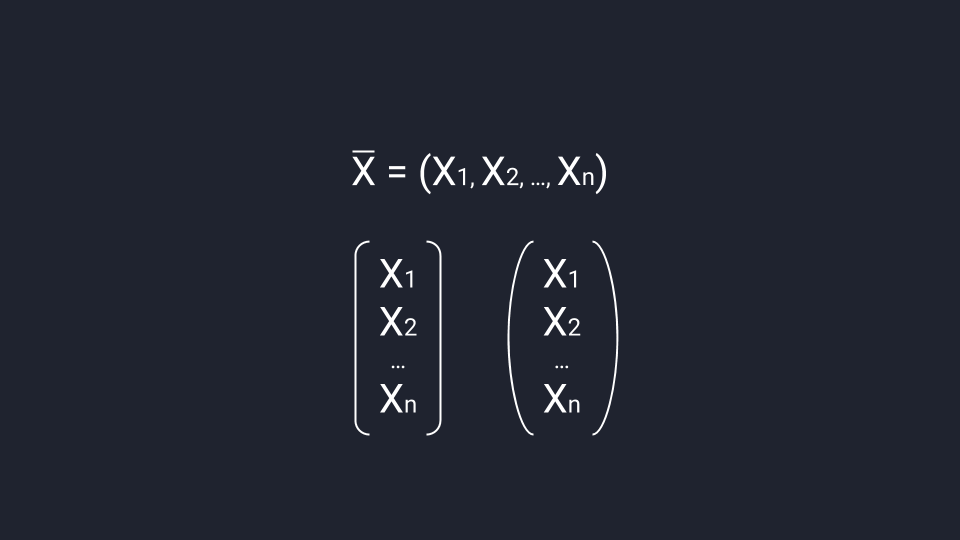
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:vector | Библиотека стандартных шаблонов (stl) | Уроки | C++ | #1Скачать

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

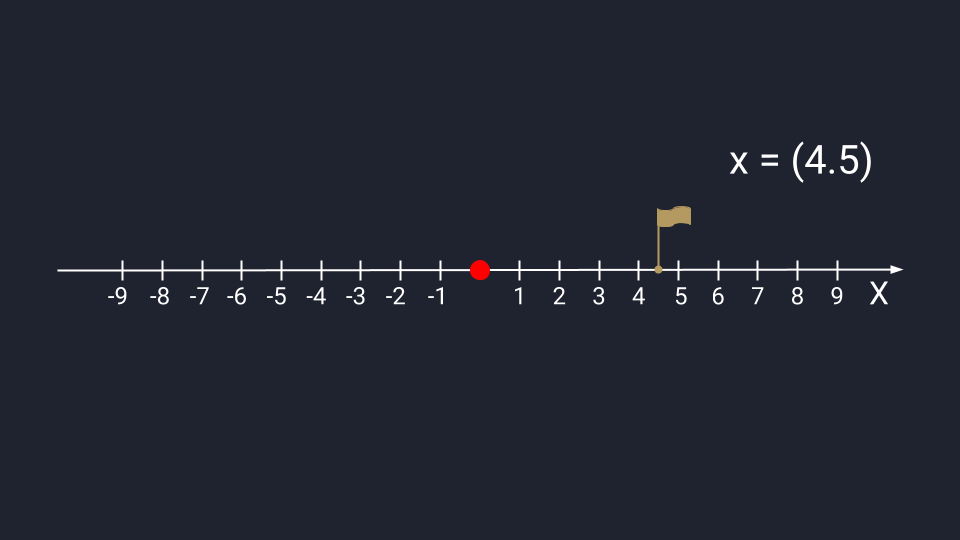
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

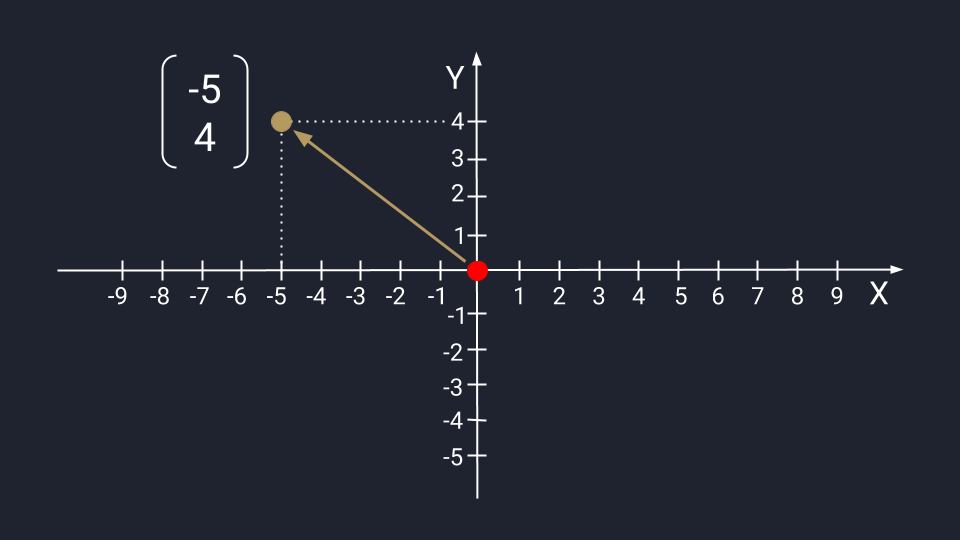
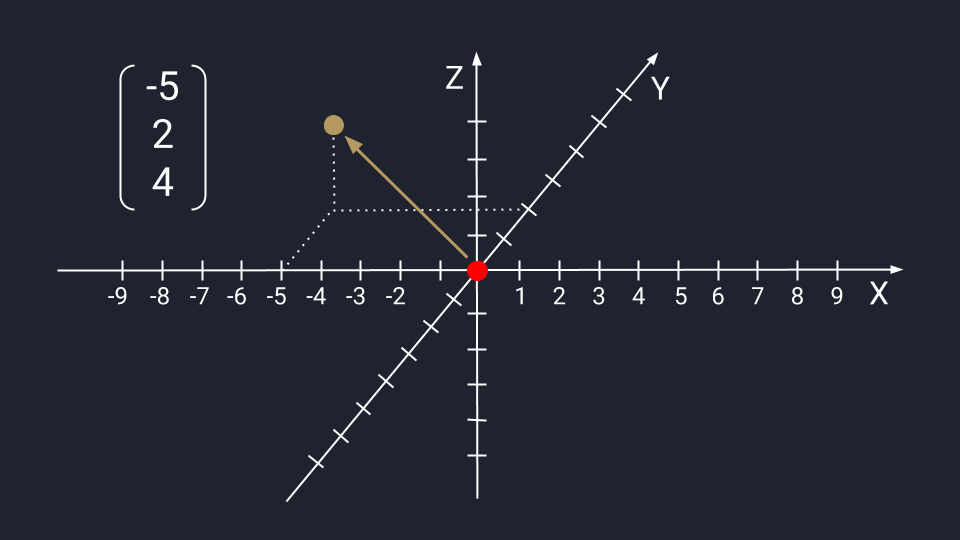
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:Двумерный массив что это. Многомерные массивы. Пример. Теория. Что такое массив. Array. C++ #30Скачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Видео:Разложение вектора по базису. 9 класс.Скачать

n-мерные векторы, операции над ними.

В разделе векторы — основные определения мы ввели понятие вектора в двумерном пространстве (на плоскости) и в трехмерном пространстве. В этой статье мы отойдем от геометрического толкования вектора и посмотрим на него не как на направленный отрезок, а как на упорядоченный набор чисел с присущими ему свойствами. То есть, мы рассматрим векторы с позиций алгебры, что позволит расширить понятие вектора на случай n -мерного пространства. Итак, мы дадим понятие n -мерного вектора, зададим операции над n -мерными векторами, перечислим свойства этих операций и покажем их применение при решении задач.

Упорядоченная совокупность n действительных или комплексных чисел называется n-мерным вектором.

Числа называются координатами вектора.

Векторы обозначаются строчными латинскими буквами, например, a, b, c и т.п., координаты вектора указываются в скобках.

Если записать вектор a как , то имеем вектор-строку; если записать , то имеем вектор-столбец. Это две формы записи одного и того же объекта — n -мерного вектора.

Обратите внимание: при обозначении n -мерных векторов стрелочка сверху над буквой (которая ставится при обозначении вектора на плоскости и в трехмерном пространстве) отсутствует.

Вектор , все координаты которого равны нулю, называют нулевым вектором.

Вектор называется противоположным вектору .

Для n -мерных векторов задаются две операции: сложение векторов и умножение вектора на число.

Суммой двух векторов и называется вектор, координаты которого равны сумме соответствующих координат, то есть, .

Следует отметить, что складывать можно только векторы количество координат которых совпадает. Операция сложения для векторов, имеющих различное число координат, не определена.

Произведением действительного или комплексного числа и вектора называется вектор, координаты которого равны соответствующим координатам вектора а , умноженным на , то есть, .

Введенные таким образом операции над n -мерными векторами при n=2 и n=3 полностью согласуются с операциями сложения и умножения вектора на число на плоскости и в трехмерном пространстве в геометрическом смысле. Под координатами двумерного или трехмерного вектора в этом случае понимаем координаты вектора в заданной прямоугольной системе координат на плоскости или в пространстве соответственно.

Перечислим свойства операций над n -мерными векторами.

Для любых векторов и произвольных действительных или комплексных чисел справедливо:

свойство коммутативности сложения векторов a+b=b+a ;
свойство ассоциативности векторов (a+b)+c=a+(b+c) ;
существует нейтральный вектор по операции сложения, им является нулевой вектор, a+0=a ;
для любого вектора существует противоположный вектор, которые в сумме дают нулевой вектор a+(-a)=0 ;
Сочетательное свойство умножения .
Первое распределительное свойство .
Второе распределительное свойство .
существует нейтральное число по операции умножения, им является единица .

Эти свойства справедливы в силу свойств операций сложения и умножения действительных или комплексных чисел.

Операции вычитания векторов как таковой нет, так как разность векторов a и b есть сумма векторов a и -b .

Перечисленные свойства операций позволяют выполнять преобразования в выражениях содержащих векторы по тем же принципам, что и в числовых выражениях.

Рассмотрим несколько примеров.

Даны векторы . Найдите сумму и разность векторов a и b .

Суммой двух векторов является вектор, координаты которого равны сумме соответствующих координат:

Разность векторов a и b есть сумма вектора а и вектора b , предварительного умноженного на минус единицу: . Сначала выполняется умножение вектора на число:

Осталось выполнить сложение:

Даны векторы . Найдите вектор .

Сначала упростим выражение, используя свойства операций над векторами:

Теперь найдем координаты полученного вектора:

Даны векторы . Найдите координаты вектора , выполнив необходимые операции.

При нахождении координат вектора сначала выполним умножение вектора e на число 2 , далее просуммируем соответствующие координаты:

Даны векторы . Выполните указанные действия .

Вектор имеет четыре координаты, а вектор — три, поэтому мы не можем их сложить и, следовательно, не можем выполнить действия над векторами .

Мы не можем выполнить указанные действия с заданными векторами.

Множество всех n -мерных векторов с введенными операциями сложения векторов и умножения вектора на число порождают линейное пространство.

Линейное пространство, элементами которого являются векторы, называется векторным или арифметическим.

Мы дали понятие n -мерного вектора, рассмотрели операции над n -мерными векторами, их свойства и увидели, что множество всех n -мерных векторов с определенными на нем операциями сложения и умножения на число порождают векторное пространство.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Векторы в C++: для начинающих

Всем привет! До этого дня мы использовали чистые массивы. Чистые — это значит простые массивы, не имеющие у себя в багаже различных функций. В этом уроке мы пройдем нечистые массивы — векторы.

Быстрый переход по статье:

Видео:Что такое векторный базис? Душкин объяснитСкачать

Что такое вектор (vector)

Вектор — это структура данных, которая уже является моделью динамического массива.

Давайте вспомним о том, что для создания динамического массива (вручную) нам нужно пользоваться конструктором new и вдобавок указателями. Но в случае с векторами всего этого делать не нужно.
Вообще, по стандарту пользоваться динамическим массивом через конструктор new — не есть правильно. Так как в компьютере могут происходить различные утечки памяти.

Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Как создать вектор (vector) в C++

Сначала для создания вектора нам понадобится подключить библиотеку — , в ней хранится шаблон вектора.

Кстати, сейчас и в будущем мы будем использовать именно шаблон вектора. Например, очередь или стек, не созданные с помощью массива или вектора, тоже являются шаблонными.

Далее, чтобы объявить вектор, нужно пользоваться конструкцией ниже:

Вначале пишем слово vector .
Далее в угольных скобках указываем тип, которым будем заполнять ячейки.
И в самом конце указываем имя вектора.

В примере выше мы создали вектор строк.

Кстати, заполнить вектор можно еще при инициализации (другие способы мы пройдем позже — в методах вектора). Делается это также просто, как и в массивах. Вот так:

После имени вектора ставим знак равенства и скобки, в которых через пробел указываем значение элементов.

Такой способ инициализации можно использовать только в C++!

Так, чтобы заполнить вектор строками, нам нужно использовать кавычки — «строка» .

Второй способ обратиться к ячейке

Мы знаем, что в векторе для обращения к ячейке используются индексы. Обычно мы их используем совместно с квадратными скобками [] .

Но в C++ есть еще один способ это сделать благодаря функции — at(). В скобках мы должны указать индекс той ячейки, к которой нужно обратиться.

Вот как она работает на практике:

Давайте запустим эту программу:

Как указать количество ячеек для вектора

Указывать размер вектора можно по-разному. Можно это сделать еще при его инициализации, а можно хоть в самом конце программы. Вот, например, способ указать длину вектора на старте:

Так в круглых скобках () после имени вектора указываем первоначальную длину. А вот второй способ:

Первая строчка нам уже знакома. А вот во второй присутствует незнакомое слово — reserve , это функция, с помощью которой мы говорим компилятору, какое количество ячеек нам нужно использовать.

Вы можете задать логичный вопрос:»А в чем разница?». Давайте создадим два вектора и по-разному укажем их количество ячеек.

Как видим, в первом случае мы вывели три нуля, а во втором: 17, 0, 0.

Все потому, что при использовании первого способа все ячейки автоматически заполнились нулями.

При объявлении чего-либо (массива, вектора, переменной и т.д) мы выделяем определенное количество ячеек памяти, в которых уже хранится ненужный для ПК мусор. В нашем случае этим мусором являются числа.

Поэтому, когда мы вывели второй вектор, в нем уже находились какие-то рандомные числа — 17, 0, 0. Обычно они намного больше. Можете кстати попробовать создать переменную и вывести ее значение.

Нужно помнить! При использовании второго способа есть некоторый плюс — по времени. Так как для первого способа компилятор тратит время, чтобы заполнить все ячейки нулями.

Видео:Радиус векторСкачать