Образуют ли точки треугольник (3 видео) | Курс школьной геометрии

Проверьте, являются ли три точки более линейными или нет

У меня есть проблема, чтобы проверить, образуют ли три точки треугольник или нет. Если он образует треугольник, программа должна напечатать квадрат максимальной длины трех сторон треугольника. Если нет, программа выведет «Coolinear».
В любом случае вот пример того, что я пробовал:

Я разместил этот код на сайте codeforces, так как это моя последняя проблема на конкурсе. Это дает мне неправильный ответ на тесте 9, Что еще я должен использовать? и почему мой ответ неверен?

В любом случае вот текст проблемы:
Как и все решатели проблем, Meiko любит есть креп! Как мы все знаем, креп обычно подают в треугольной форме. Теперь Мейко хочет знать, насколько большой может быть сторона крепа! Поэтому он пытается нарисовать треугольник на плоскости, используя три точки, и рассчитать максимальную длину трех сторон треугольника. Но иногда он засыпает, так как он был занят командой, готовящей тренировочные задачи! В результате три точки, которые он использует, могут не образовывать треугольник, который может представлять кусок крепа! Треугольник может представлять кусок крепа, только если он имеет положительную площадь. Так что вы здесь, чтобы помочь Meiko! Учитывая координаты, используемые Мейко, определите, образуют ли они треугольник, который может представлять кусок крепа или нет.

вход
Три целочисленных координаты (X, Y), которые представляют три точки, используемые Мейко. Каждая точка на отдельной линии. (-10 ^ 9 if -отношения должны быть исправлены

Содержание

Другие решения
Определение принадлежности точки треугольнику
Метод сравнения площадей
Метод относительности
Всё относительно!
Векторный метод
Что такое треугольник
Определение треугольника
Свойства сторон и углов треугольника
Примеры решения задач
🎦 Видео

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Другие решения

Ваш код будет выводить несколько результатов, если максимальная длина не уникальна.

Вы можете избавиться от сложной логики:

Позднее приложение, если это еще не решено (и я не могу спать):

Ключом к решению этой проблемы является слово «целые числа» в описании.
Тестовый пример, на котором вы терпите неудачу, построен так, что

не равен нулю при использовании чисел с плавающей запятой и нулю при использовании целых чисел

Вам не нужно 0.5 * abs(. определить, является ли область нулевой или нет, и я ожидаю, что следующее будет работать:

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Определение принадлежности точки треугольнику

Дано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты.

Что нужно узнать: нужно установить принадлежность точки треугольнику.

В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику.

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Метод сравнения площадей

В данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно.

Затем находится площадь самого треугольника ABC.

Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность.

Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий.

Простейшая реализация алгоритма:

Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить.

Видео:Алгоритмы. Попадание точки в треугольникСкачать

Метод относительности

Данный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.

На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику.

Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Всё относительно!

Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой.

Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику.

Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции!

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Векторный метод

Третий метод который я освещаю для меня самый интересный.

Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма…

Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :]

1) одну вершину треугольника помещаем в координаты (0;0);

2) две стороны, выходящие из этой вершины, представляем как вектора.

Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)

Рис. 4.

Видео:✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

Что такое треугольник

Видео:Почему простые числа образуют спирали? [3Blue1Brown]Скачать

Определение треугольника

Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, трех отрезков, которые последовательно соединяют эти точки и ограниченной ними части плоскости.

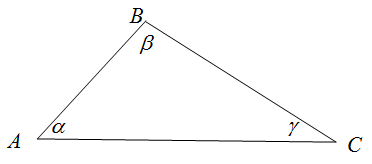
Точки $A$, $B$ и $C$ называются lt strong>вершинами lt /strong>, а отрезки $AB$, $BC$, $AC$ — сторонами треугольника.

Углы $angle A B C, angle B A C, angle A C B$ — углы треугольника $triangle A B C$. Их можно обозначать также одной буквой: $angle A, angle B, angle C$ или $alpha, beta, gamma$ — соответственно. Стороны, которые лежат против углов $angle A, angle B, angle C$ также обозначают $a, b, c$.

Видео:Вычислить определитель 3 порядка. Правило треугольникаСкачать

Свойства сторон и углов треугольника

Любая сторона треугольника меньше суммы двух других её сторон и больше их разности:

$$c-b lt a lt c+b, c>b$$

Чтобы проверить, могут ли заданные три отрезка $a$, $b$ и $c$ образовать треугольник, достаточно проверить будет ли самый длинный отрезок меньше суммы длин двух других отрезков.

Сумма углов любого треугольника равна $180^$.

Видео:№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

Примеры решения задач

Задание. Проверить могут ли данные отрезки образовывать треугольник:

Решение. 1) Наибольшим из этих отрезков является отрезок $b=4$, сумма двух других $a+c=3+2=5$, получаем $b lt a +c$. Значит, отрезки $a=3 ; b=4 ; c=2$ образуют треугольник.

2) Среди отрезков $a=3 ; b=4 ; c=7$, наибольшим является отрезок $c=7$. Сумма оставшихся $a+b=3+4=7$. Получаем $c=a+b$, поэтому отрезки $a=3 ; b=4 ; c=7$ не могут образовывать треугольник.

Ответ. Oтрезки $a=3 ; b=4 ; c=2$ образуют треугольник.

Отрезки $a=3 ; b=4 ; c=7$ не могут образовывать треугольник.