Объем тела вращения окружности

1. О применении определённого интеграла для нахождения объёмов тел вращения

1.1. Формула объёма тела вращения

В п.16.2 дано определение тела вращения.

Получим формулу для вычисления объёма тела вращения, применяя интеграл, о котором вам рассказали в курсе «Алгебры и начал математического анализа».

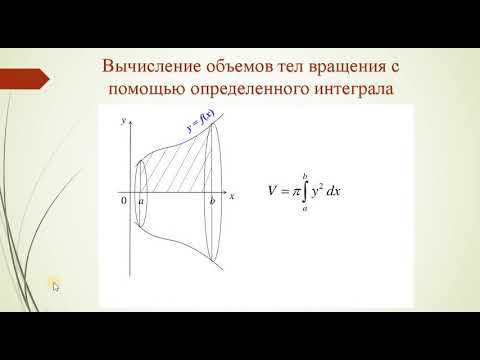
Пусть f ( x ) — непрерывная на отрезке [ a ; b ] функция, не принимающая отрицательных значений; А, В — точки графика этой функции (рис. 225).

Рассмотрим криволинейную трапецию aABb, ограниченную кривой графика функции y = f ( x ), отрезками aA, bB и отрезком [ a ; b ] координатной оси Ох (см. рис. 225). При вращении этой трапеции вокруг оси Ох образуется тело вращения (рис. 226), которое обозначим Ф и поставим себе задачу: найти объём этого тела.

Через произвольную точку х = с ( a ⩽ с ⩽ b ) отрезка [ a ; b ] проведём плоскость, перпендикулярную оси Ox. Сечением тела Ф этой плоскостью является круг, радиус которого равен f ( с ), а площадь — π f 2 ( с ) (или точка ( c ; 0)).

Объём части тела Ф , заключённой между этой плоскостью и плоскостью х = a, изменяется при изменении x. Обозначим этот переменный объём V ( х ) . Заметим, что V ( x ) = V ( a ) = 0 при х = a ; при х = b имеем V ( x ) = V ( b ) = V — искомый объём тела вращения Ф .

Покажем, что функция V ( x ) имеет производную V ′ ( х ) и V ′ ( х ) = π f 2 ( х ) .

Придадим абсциссе х приращение ∆ х > 0, тогда объём V ( х ) получает приращение ∆ V ( х ) = V ( x + ∆ x ) – V ( x ) . Пусть m и М — соответственно наименьшее и наибольшее значения функции f ( х ) на промежутке [ х ; х + ∆ х ] . Цилиндр, радиус основания которого равен m, содержится в теле вращения объёма ∆ V ( x ) , а цилиндр, радиус основания которого равен M , содержит тело объёма ∆ V ( х ); образующие цилиндров параллельны оси Ох и имеют длину, равную ∆ х . Объёмы этих цилиндров равны соответственно π m 2 • ∆ x и π M 2 • ∆ х . На основании свойства 2 объёмов (п. 10.1) получаем

π m 2 • ∆ x ⩽ ∆ V ( x ) ⩽ π M 2 • ∆ x,

π m 2 ⩽ ⩽ π M 2 .

Рассуждения для случая ∆ х ∆ х 0. Имеем m = M = f ( x ) , тогда

π m 2 ⩽ ⩽ π M 2

π f 2 ( х ) ⩽ ⩽ π f 2 ( x ) .

Значит, = π f 2 ( х ). По определению производной функции = V ′ ( x ) . Поэтому V ′ ( x ) = π f 2 ( х ), следовательно, V ( х ) — первообразная для π f 2 ( х ).

Таким образом, переменный объём V ( x ) телa вращения представляет собой одну из первообразных для функции π f 2 ( х ) на отрезке [ a ; b ]. Эта первообразная обладает тем свойством, что при х = a она обращается в нуль ( V ( a ) = 0), а при х = b значение функции V ( x ) равно объёму тела вращения Ф ( V ( b ) = V ) .

Если F ( х ) — также некоторая первообразная для функции π f 2 ( x ) , то V ( x ) = F ( x ) + С, где С — произвольная постоянная. Так как V ( a ) = 0, то из равенства V ( a ) = F ( a ) + C = 0 находим С = – F ( a ). Значит, V ( x ) = F ( x ) – F ( a ). Toгдa V ( b ) = F ( b ) – F ( a ). Ho V ( b ) = V — искомый объём тела вращения Ф . Таким образом, V = F ( b ) – F ( a ) , где F ( b ) и F ( a ) — значения первообразной для функции π f 2 ( х ) соответственно при х = b и х = a. Это означает, что

V = f 2 ( x ) dx = π ( x ) dx.

Вот почему объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = f ( x ), х = a, х = b, у = 0, вычисляется по формуле

V = ( x ) dx . (*)

ЗАДАЧА. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = , х = 0, x = 2 и y = 0 (рис. 227).

Решени е. Воспользуемся формулой V = π ( x ) dx, для чего из уравнения у = находим y 2 = 2 х. Тогда получаем

V = π dx = 2 π • = = 4 π .

1.2. Объёмы конуса, шара и его частей

Используя формулу V = ( x ) dx вычисления объёма тела вращения, получим формулы для вычисления объёма каждого изученного ранее тела вращения.

а) Объём конуса и усечённого конуса

Теорема 1 ( об объёме полного конуса ). Объём V конуса с высотой Н и радиусом основания R равен одной трети произведения площади основания на высоту :

V = R 2 Н.

Доказательств о. Конус с высотой Н и радиусом основания R можно рассматривать как тело, образованное вращением вокруг оси Ox прямоугольного треугольника с вершинами О (0; 0), А ( Н ; 0) и B ( Н ; R ) (рис. 228). Треугольник АОВ является частным случаем криволинейной трапеции, которая ограничена графиком функции у = х (0 ⩽ х ⩽ H ), осью Ох и отрезком прямой х = Н. Поэтому, используя формулу (*) п. 1.1 «Дополнений» для объёма V конуса, получаем:

V = dx = π • = π R 2 H,

где π R 2 — площадь основания конуса. Теорема доказана. ▼

Теорема 2 ( об объёме усечённого конуса ). Объём усечённого конуса с высотой Н и радиусами оснований r и R равен сумме объёмов трёх конусов с высотой Н , радиусы оснований которых соответственно равны r , R и :

V = ( r 2 + R 2 + rR ) H.

Доказательств о. Усечённый конус с высотой H и радиусами оснований r и R можно получить, вращая вокруг оси Oх прямоугольную трапецию OABC, где O (0; 0), A (0; r ), В ( Н ; R ) , С ( H ; 0) (рис. 229).

Рис. 229

Прямая AВ проходит через точки (0; r ) и ( Н ; R ), поэтому её уравнение имеет вид у = х + r. Следовательно, трапеция ОАВС ограничена графиком функции y = х + r (0 ⩽ х ⩽ Н ) , осью Oх и отрезками прямых х = 0 и х = Н. Поэтому, используя формулу (*) из п. 1.1 для объёма V усечённого конуса, получаем:

V = dx. (1)

Для вычисления интеграла сделаем замену переменных

x + r = t. (2)

Тогда dx = dt, откуда dx = dt. Новые пределы интегрирования (по переменной t ) найдём посредством подстановки формулы (2): х = 0 ⇒ t = r ; х = Н ⇒ t = R. Таким образом, для объёма V усечённого конуса получаем:

V = t 2 dt = • = • ( R 3 – r 3 ) =
= ( r 2 + R 2 + rR ) ,

что и требовалось доказать. ▼

б) Объём шарового слоя

В прямоугольной декартовой системе координат Оху рассмотрим криволинейную трапецию aABb, ограниченную дугой окружности х 2 + у 2 = R 2 , –R ⩽ a ⩽ х ⩽ b ⩽ R, отрезком [ a ; b ] оси Ох и отрезками aА и bВ прямых соответственно x = a и х = b (рис. 230, а ) .

Рис. 230

При вращении криволинейной трапеции aАВb вокруг оси Ох образуется шаровой слой (рис. 230, б ). Найдём его объём, применяя формулу (*) п. 1.1.

Из уравнения х 2 + у 2 = R 2 имеем у 2 = R 2 – x 2 . Поэтому для вычисления объёма V шарового слоя получаем:

V = dx = = =
=

Таким образом, объём шарового слоя, отсекаемого от шара x 2 + y 2 + z 2 ⩽ R 2 радиуса R плоскостями x = a и x = b, вычисляется пo формуле

V = (**)

Пусть радиусы оснований шарового слоя равны r 1 и r 2 ( r 1 > r 2 ), а высота — H (см. рис. 230, a ).

Тогда Н = b – a, = R 2 – a 2 , = R 2 – b 2 .

Формулу (**) преобразуем к виду:

V = (3 R 2 – ( b 2 + ab + a 2 )) =
= (( R 2 – b 2 ) + ( R 2 – ab ) + ( R 2 – a 2 )).

Из системы равенств ( b – a ) 2 = H 2 , R 2 – a 2 = , R 2 – b 2 = после почленного сложения их левых и правых частей находим:

R 2 – ab = .

V = (( R 2 – b 2 ) + ( R 2 – ab ) + ( R 2 – a 2 )) =
= .

Таким образом, объём шарового слоя с радиусами оснований r 1 и r 2 и высотой Н вычисляется по формуле

V = . (***)

При вращении полукруга х 2 + у 2 = R 2 (расположенного в плоскости Оху, рис. 231, а ) вокруг оси Ох образуется шар радиуса R (рис. 231, б ). Из уравнения окружности х 2 + y 2 = R 2 данного полукруга имеем у 2 = R 2 – х 2 . Тогда, полагая a = –R, b = R в формуле (*) п. 1.1, находим объём V шара радиуса R :

V ш = =
= .

Таким образом, имеет место следующая теорема.

Теорема 3 ( об объёме шара ). Объём шара радиуса R вычисляется по формуле

V ш = .

г) Объём шарового сегмента

Если b = R (см. п. 1.2, б), то получаем криволинейную трапецию aAB (рис. 232, а ), при вращении которой вокруг оси Ох образуется шаровой сегмент (рис. 232, б ).

Пусть высота шарового сегмента равна Н, тогда a = R – Н. Так как дуга AВ криволинейной трапеции aАВ является частью окружности x 2 + y 2 = R 2 (в плоскости Оxу ) , то формулу объёма шарового сегмента получим по аналогии с выводом формулы для вычисления объёма шара, учитывая при этом, что пределы a и b интегрирования равны: a = R – H , b = R, т. е.

V ш. сегм = =
=

Таким образом, имеет место следующая теорема.

Теорема 4 ( об объёме шарового сегмента ). Объём шарового сегмента, отсекаемого от шара радиуса R и имеющего высоту Н , вычисляется по формуле

V ш. сегм =

Если в формуле (***) п. 1.2, б положить r 2 = 0, r 1 = r, то получим формулу для вычисления объёма шарового сегмента с радиусом основания r и высотой Н :

V ш. сегм = (3 r 2 + H 2 ) .

д) Объём шарового сектора

Шаровой сектор состоит из конуса с вершиной в центре шара и шарового сегмента, имеющего с конусом общее основание (риc. 233). Пусть R = ОА — радиус шара; АС = r — радиус основания шарового сегмента, NC = H — его высота; N — точка сферы (рис. 233).

Найдём объёмы конуса и шарового сегмента, учитывая, что высота h конуса равна OC = ON – CN = R – Н.

Объём V к конуса равен

π • АС 2 • ОС = π r 2 ( R – Н ) .

Выразим r 2 через R и H.

B прямоугольном треугольнике AOC находим r 2 = AC 2 = ОА 2 – OC 2 = R 2 – ( R – H ) 2 = H (2 R – H ).

V к = π H (2 R – H )( R – H ) = (2 R 2 – 3 RH + H 2 ) .

Для объёма шарового сегмента имеем:

V ш. сегм = (3 AC 2 + NC 2 ) = (3 H (2 R – H ) + H 2 ) =
= (3 RН – H 2 ) .

Тогда для объёма шарового сектора получаем

V ш. сект = V к + V ш. сегм =
= (2 R 2 – 3 RH + H 2 ) + (3 RH – H 2 ) = π R 2 H.

Таким образом, доказана следующая теорема.

Теорема 5 ( об объёме шарового сектора ). Объём шарового сектора шара радиуса R вычисляется по формуле

V ш. сект = R 2 H ,

где Н — длина высоты шарового сегмента, соответствующего данному шаровому сектору.

В курсе математического анализа, который вам предстоит изучать в высшей школе, будет дано строгое обоснование применения определённого интеграла не только для нахождения объёмов тел, но и для нахождения площадей поверхностей и длин дуг линий. Решите самостоятельно следующие задачи.

1) Найдите объём тела, которое получается при вращении вокруг оси Ох криволинейной трапеции, ограниченной гиперболой у = , прямыми х = 3, х = 12 и осью абсцисс. ( Ответ: 4 π .)

2) Найдите объём тела, образованного вращением вокруг оси Oх фигуры, ограниченной одной полуволной синусоиды у = sin x и отрезком 0 ⩽ х ⩽ π оси абсцисс. ( Ответ: 0,5 π 2 . )

3) Найдите объём тела, полученного при вращении кривой у = 0,25 х 2 вокруг оси Оу в пределах от у = 1 до у = 5. ( Ответ: 48 π .)

4) Найдите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми у = 2 х 2 и у = x 3 .

Объем тела вращения онлайн

Рассмотрим некоторую функцию , непрерывную на отрезке :

Если мы будем вращать данную функцию вокруг оси , то образуется некоторое тело вращения:

Объём полученной фигуры можно посчитать, вычислив вот такой интеграл:

Теперь рассмотрим некоторую функцию , непрерывную на отрезке :

На этот раз будем вращать данную функцию вокруг оси . В результате получим следующее тело вращения:

Его объём вычисляется по формуле:

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет вычислить объём тела вращения, заданного практически любой функцией. Для этого, в калькулятор нужно ввести саму функцию, границы в пределах которых будет вычисляться объём тела и выбрать ось вращения.

Конспекты по математике на тему «Тела вращения. Объемы тел вращения»

Конспекты занятий по математике для студентов первого курса теме «Тела вращения. Объемы тел вращения».

Тела вращения — объёмные тела, полученные при вращении плоской фигуры вокруг своей оси или стороны.

Примеры тел вращения: цилиндр, конус, шар, сфера.

Цили́ндр (от греч. kýlindros, валик, каток) — геометрическое тело, образованное вращением прямоугольника вокруг одной из сторон.

Цилиндр состоит из двух параллельных кругов, не лежащих в одной плоскости, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, — образующими цилиндра.

Примеры тел, имеющих цилиндрическую форму: часть водопроводной трубы, консервная банка.

Радиусом цилиндра называется радиус его основания.

Высотой цилиндра называется расстояние между его основаниями.

Осью цилиндра называется прямая, проходящая через центр оснований, параллельно образующим.

Осевое сечение – сечение цилиндра плоскостью, проходящей через его ось.

Поверхность цилиндра состоит из оснований и боковой поверхности.

Боковая поверхность составлена из образующих.

Цилиндр называется прямым , если его образующие перпендикулярны плоскостям оснований.

Основания цилиндра равны и параллельны.

Образующие цилиндра равны и параллельны.

Ко́нус — тело вращения, образованное вращением прямоугольного треугольника, вокруг одного из его катетов.

Конус состоит из круга – основания конуса, вершины конуса — точки, не лежащей в плоскости основания, и всех отрезков, соединяющих вершину конуса с точками основания.

Примеры тел, имеющих форму конуса: воронка для наливания жидкости, чум — жилье народов севера, мороженое-рожок.

Отрезок, соединяющий вершину и границу основания, называется образующей конуса .

Боковая поверхность конуса — объединение образующих конуса.

Отрезок, опущенный перпендикулярно из вершины на плоскость основания, называется высотой конуса .

Конус называется прямым , если прямая ( ось конуса ), соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.

Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением .

Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом .

Шар — тело вращения, полученное вращением полукруга около его неподвижного диаметра.

Примеры тел, имеющих форму шара или сферы: мыльный пузырь, земля, футбольный и теннисный мячи.

Любой отрезок, соединяющий центр шара с точкой его поверхности, называется радиусом .

Сфера это поверхность шара .

Отрезок, соединяющий две точки шаровой поверхности и проходящей через центр шара, называется диаметром .

Концы любого диаметра называются диаметрально противоположными точками шара.

Диаметр называется осью шара , а его оба конца — полюсами шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью.

Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью . Точка А называется точкой касания .

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом . Другие плоские сечения шара называются малыми кругами.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

1. Уравнение шара с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 ≤ R 2

2. Уравнение шара с радиусом R и центром в точке с координатами (x ₀ , y ₀ , z ₀ ) в декартовой системе координат :

(x — x ₀ ) 2 + (y — y ₀ ) 2 + (z — z ₀ ) 2 ≤ R 2

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 = R 2

2. Уравнение сферы с радиусом R и центром в точке с координатами (x ₀ , y ₀ , z ₀ ) в декартовой системе координат :

(x — x ₀ ) 2 + (y — y ₀ ) 2 + (z — z ₀ ) 2 = R 2

Формулы объема цилиндра, конуса и шара.

Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.

Объем прямого цилиндра равен произведению площади основания на высоту: V = S _осн h , т.к. в основании цилиндра лежит круг, то S _осн = S _круга =π R 2 . Тогда формула объема цилиндра примет вид: V = π R 2 h .

Конус — геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.

Объем конуса равен одной трети произведения площади основания на высоту V = S _осн h , т.к. в основании конуса лежит круг, то S _осн =S _круга =πR 2 . Тогда формула объема цилиндра примет вид: V = πR 2 h .

3. Объем усеченного конуса.

Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

Шар — это геометрическое тело, состоящее из точек пространства, которые удалены от центра O на одинаковое расстояние R .

Объем шара радиуса R равен V = π R 3 .