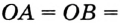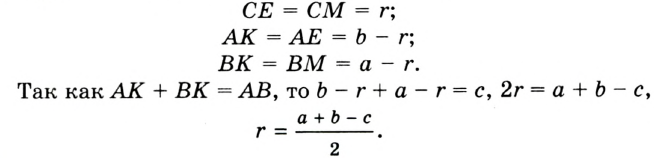- Ваш ответ
- решение вопроса
- Похожие вопросы
- Решение задач по теме «Перпендикуляр и наклонные»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Дистанционные курсы для педагогов
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Описанные и вписанные окружности — формулы, свойства и определение с примерами решения
- Описанная и вписанная окружности треугольника
- Прямоугольный треугольник и его описанная и вписанная окружности
- Вписанные и описанные четырехугольники
- Окружность, вписанная в треугольник
- Описанная трапеция
- Дополнительные свойства и признаки вписанного четырехугольника
- Обобщенная теорема Пифагора
- Формула Эйлера для окружностей
- Справочная информация по описанной и вписанной окружности треугольника
- 🔥 Видео
Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Ваш ответ
Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

решение вопроса
Видео:Геометрия Точка O центр окружности вписанной в треугольник ABC BC = a AC = b угол AOB = 120 НайдитеСкачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,868
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Вписанная окружностьСкачать

Решение задач по теме «Перпендикуляр и наклонные»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Задание 16 ЕГЭ по математикеСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Решение задач по теме «Перпендикуляр и наклонные» Задачи на готовых чертежах
Дано: АВ- перпендикуляр, АС и AD-наклонные, АСВ=30°, АС=16, ВD=6 Найти: АD 1 Ответ: 10 А В D C 30° 16 6
Дано: АВ- перпендикуляр, АС и AD-наклонные, АСВ=45°, АС= , ВD=6 Найти: АD 2 Ответ: 10 А В D C 45° 6
Дано: АВ- перпендикуляр, АС и AD-наклонные, АСВ=60°, АС= 4, ВD= Найти: АD 4 3 Ответ: 5 А В D C 60°
Решение задач по теме «Перпендикуляр и наклонные» Задачи на готовых чертежах
Дано: АВ- перпендикуляр к плоскости , АС и AD-наклонные, АСВ= 30°, АDB= 60°, СВD= 90°, АВ=1 Найти: РCAD 4 Ответ: 1 А В C D 60° 30°
Дано: АВ- перпендикуляр к плоскости , АС и AD-наклонные, АСВ= АDB= 30°, САD= 60°, RACD= Найти: AB 60° 5 Ответ: 1,5 А В C D 30° 30°
Дано: ABCD-трапеция, О- центр окружности, описанной вокруг трапеции, ОЕ (АВС), АЕ=10, ОЕ=8, ВАD=30° Найти: BD. О 6 6 Ответ: А В С D E 8 10 30°
Дано: АВС, О- центр вписанной окружности, OD (ABC), АС=ВС=5, АВ=6, DO=1, АМ=МВ Найти: DM. 1 7 Ответ: А В С D О М 6 5
С Дано: АВС, АСВ=90°, О — центр описанной окружности, АМ=МС, OD (АВС), АВ=5, АС=3, DO= Найти: МD. 4 8 Ответ: А В D О М 3 5
Дано: АВС, ABС=90°, О- центр вписанной окружности, OD (ABC), АВ=3, ВС=4, DO= , ОМ=r Найти: DM. 2 9 Ответ: А В С D О М 3 4
D Дано: АВС, ACB=90°, О- центр вписанной окружности, OD (ABC), АС=6, ВС=8, DO= , ОМ=r Найти: 12 10 Ответ: А В С О М 6 8
Дано: АВСD-трапеция, описанная вокруг окружности с центром О, АВ=СD, ОЕ (АВС), РАВСD=16, СDА=30°, ОЕ=4, М и К-точки касания окружности со сторонами ВС и АD Найти: ЕК 4 Ответ: Р 11 А В С D О 30° К М Е
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 935 человек из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 316 человек из 70 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 696 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 478 153 материала в базе
Материал подходит для УМК
«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Дистанционные курсы для педагогов
Другие материалы
- 31.05.2018
- 3432
- 31.05.2018
- 777
- 31.05.2018
- 1038
- 31.05.2018
- 9827
- 31.05.2018
- 20254
- 31.05.2018
- 3885
- 31.05.2018
- 1372
- 31.05.2018
- 1190
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 31.05.2018 10383 —> —> —> —>
- PPTX 346.9 кбайт —> —>
- Оцените материал:
Настоящий материал опубликован пользователем Щенников Алексей Сергеевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На проекте: 5 лет и 3 месяца
- Подписчики: 2
- Всего просмотров: 458324
- Всего материалов: 115
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Дистанционные курсы
для педагогов
548 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку
Время чтения: 1 минута
Переводить ЕГЭ по математике, физике и химии в компьютерный формат пока не планируется
Время чтения: 2 минуты
Стартовал региональный этап Всероссийской олимпиады школьников
Время чтения: 2 минуты
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Порядка 65% выпускников российских вузов идут работать по специальности
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Описанные и вписанные окружности — формулы, свойства и определение с примерами решения
Содержание:
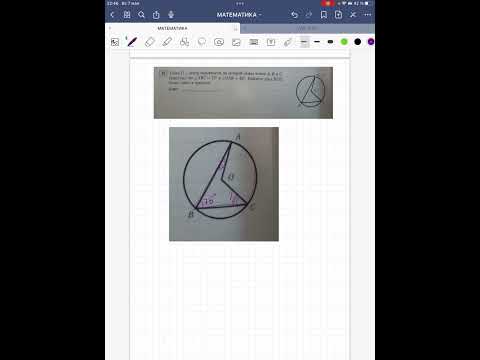
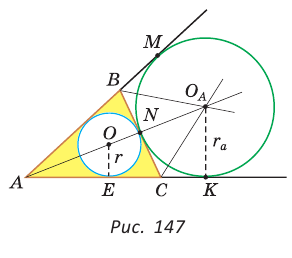
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника. На рисунке 146 изображен треугольник АВС и три его вневписанные окружности с центрами
Вневписанные окружности обладают рядом интересных свойств:
1. Центры вписанной и вневписанной окружностей лежат на биссектрисе соответствующего внутреннего угла треугольника.
2. 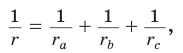
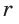
3. 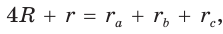
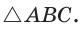
Попробуйте доказать некоторые из этих свойств.
Найдем радиус 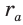
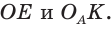
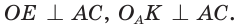
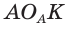
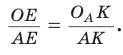
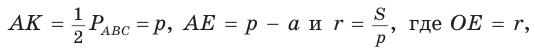
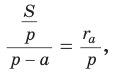
Пример:
Вычислим, используя данную формулу, радиус вневписанной окружности прямоугольного треугольника с катетами 3 и 4, которая касается гипотенузы:
Видео:№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать
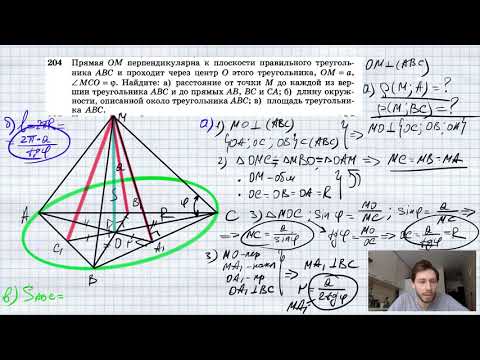
Описанная и вписанная окружности треугольника
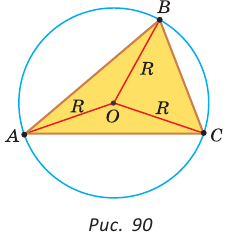
Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.
На рисунке 90 изображена окружность с радиусом R и центром 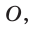
Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника.
Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС».
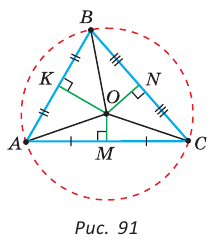
Теорема (об окружности, описанной около треугольника).
Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.
Рассмотрим произвольный треугольник АВС (рис. 91). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно.
Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них.
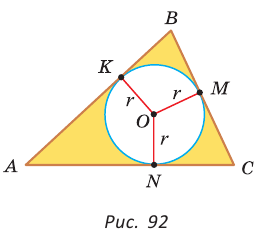
Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.
На рисунке 92 изображена окружность с центром О и радиусом 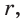
Так как 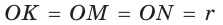
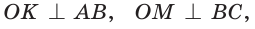
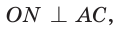
Вместо слов «окружность, вписанная в треугольник АВС», также говорят «вписанная окружность треугольника АВС».
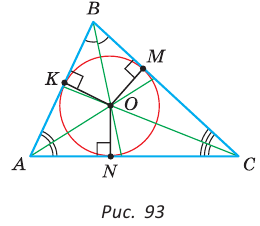
Теорема (об окружности, вписанной в треугольник).
В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.
Рассмотрим произвольный треугольник АВС (рис. 93). Пусть О — точка пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОМ и ON соответственно к сторонам АВ, ВС и АС. По свойству биссектрисы угла ОК = ON, ON = ОМ. Окружность с центром в точке О и радиусом ОК будет проходить через точки К, М и N и касаться сторон АВ, ВС и АС в указанных точках по признаку касательной.
Следовательно, эта окружность является вписанной в треугольник АВС. Единственность вписанной окружности докажите самостоятельно.
Замечание. Так как все три биссектрисы треугольника пересекаются в одной точке, то для нахождения центра вписанной окружности достаточно построить точку пересечения любых двух из них.
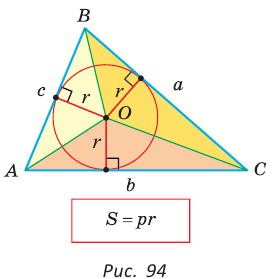
Теорема. Площадь треугольника можно найти по формуле 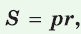
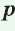
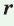
Пусть дан треугольник АВС со сторонами 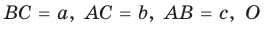
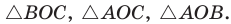
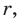
Следствие:
Радиус окружности, вписанной в треугольник, можно найти по формуле
Одной из важнейших задач данной темы является задача нахождения радиуса описанной и радиуса вписанной окружностей данного треугольника.
Пример:
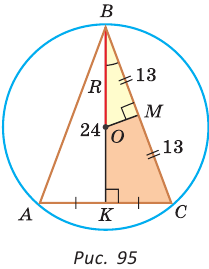
Найти радиус окружности, описанной около равнобедренного треугольника АВС, у которого АВ = ВС = 26 см, высота ВК = 24 см
(рис. 95).
Решение:
Способ 1 (метод подобия). Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Проведем серединные перпендикуляры к сторонам АС и ВС, которые пересекутся в точке О — центре описанной окружности. Так как в равнобедренном треугольнике высота, проведенная к основанию, является медианой, то ВК — серединный перпендикуляр к стороне АС. Пусть МО — серединный перпендикуляр к стороне ВС. Тогда ВМ = 13 см, ВО = R -— искомый радиус. Поскольку 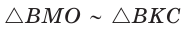
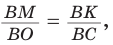
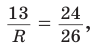
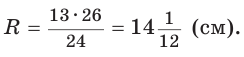
Способ 2 (тригонометрический метод). Из 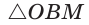
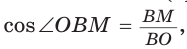
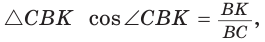
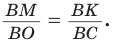
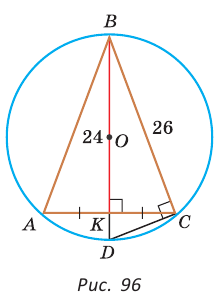
Способ 3* (среднее пропорциональное). Продлим высоту ВК до пересечения с описанной окружностью в точке D (рис. 96). Так как центр описанной окружности равнобедренного треугольника лежит на прямой ВК (см. способ 1), то BD = 2R — диаметр данной окружности. В прямоугольном треугольнике BCD 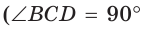
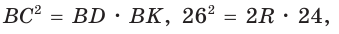
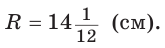
Ответ: 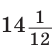
Замечание. Из решения ключевой задачи 1 следует свойство: «Центр окружности, описанной около равнобедренного треугольника, лежит на его высоте, проведенной к основанию, или на ее продолжении».
Верно и обратное утверждение: «Если центр окружности, описанной около треугольника, лежит на высоте треугольника или на ее продолжении, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Полезно запомнить!
Если в ключевой задаче 1 боковую сторону обозначить 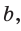
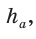
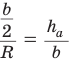
Отсюда следует удобная формула для нахождения радиуса окружности, описанной около равнобедренного треугольника:
Пример:
Найти радиус окружности, вписанной в равнобедренный треугольник АВС, у которого АВ = ВС = 10 см, АС = 12 см.
Решение:
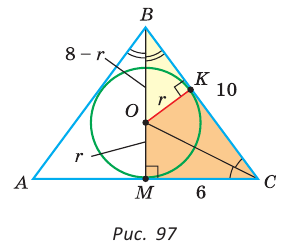
Способ 1 (метод подобия). Центр вписанной окружности находится в точке пересечения биссектрис треугольника. Проведем в треугольнике АВС биссектрисы из вершин В и С, которые пересекутся в точке О — центре вписанной окружности (рис. 97). Биссектриса ВМ, проведенная к основанию равнобедренного треугольника АВС, будет его высотой и медианой, луч СО — биссектриса угла С, 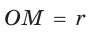
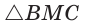
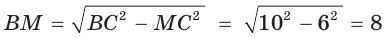
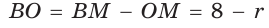
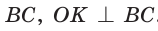
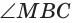
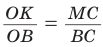
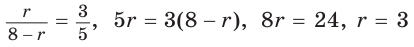
Способ 2 (тригонометрический метод). Из 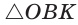
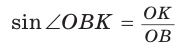
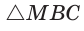
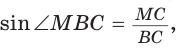
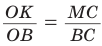
Способ 3 (свойство биссектрисы треугольника). СО — биссектриса 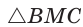
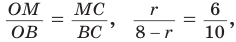
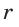
Способ 4 (формула 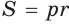
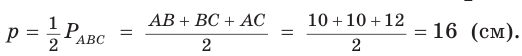
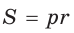
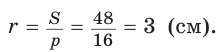
Ответ: 3 см.
Замечание. Из решения ключевой задачи 2 следует свойство: «Центр окружности, вписанной в равнобедренный треугольник, лежит на его высоте, проведенной к основанию».
Верно и обратное утверждение: «Если центр окружности, вписанной в треугольник, лежит на высоте треугольника, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Пример:
Дан равносторонний треугольник со стороной а. Найти радиус R его описанной окружности и радиус 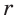
Решение:
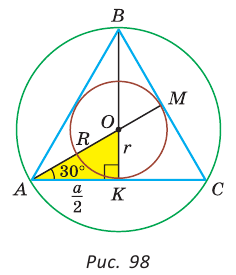
Способ 1 (тригонометрический метод).Так как в равностороннем треугольнике биссектрисы являются и высотами, и медианами, то его биссектрисы лежат на серединных перпендикулярах к сторонам треугольника. Поэтому в равностороннем треугольнике центры описанной и вписанной окружностей совпадают.
Рассмотрим равносторонний треугольник АВС со стороной а, у которого высоты AM и ВК пересекаются в точке О — центре описанной и вписанной окружностей (рис. 98). Тогда ОА = OB = R — радиусы описанной, 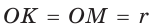
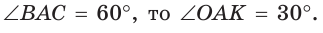
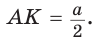
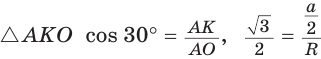
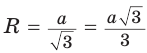
В 
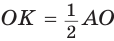
Способ 2 (свойство медиан). Поскольку AM и ВК — медианы треугольника АВС (см. рис. 98), то по свойству медиан 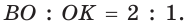
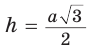
Ответ:
Полезно запомнить!
Поскольку радиус описанной окружности равностороннего треугольника 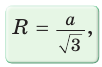
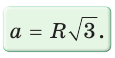
треугольника в 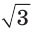
Чтобы найти радиус R описанной окружности равностороннего треугольника, нужно сторону 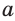
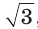
Прямоугольный треугольник и его описанная и вписанная окружности
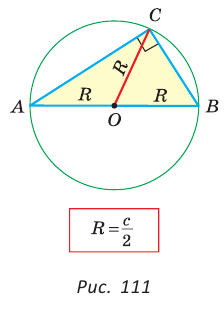
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а ее радиус равен половине гипотенузы, т. е. 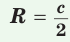
Проведем в прямоугольном треугольнике АВС медиану СО к гипотенузе АВ (рис. 111). Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы, то ОС = ОА = ОВ.
Тогда середина гипотенузы — точка О — равноудалена от точек А, В и С и поэтому является центром описанной окружности треугольника АВС. Радиус этой окружности 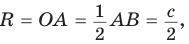
Теорема доказана.
Замечание. Также можно доказать, что серединные перпендикуляры к катетам прямоугольного треугольника пересекаются на середине гипотенузы.
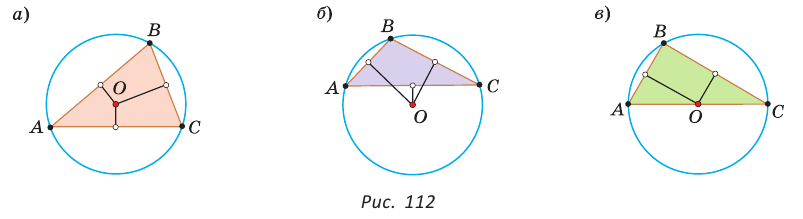
Отметим, что у остроугольного треугольника центр описанной окружности лежит внутри треугольника (рис. 112, а), у тупоугольного — вне треугольника (рис. 112, б), у прямоугольного — на середине гипотенузы (рис. 112, в). Обоснуйте первые два утверждения самостоятельно.
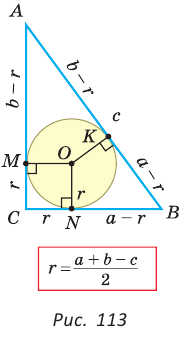
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле 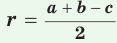
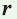
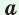
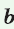
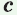
Рассмотрим прямоугольный треугольник АВС с катетами 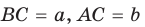
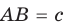
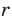
Проведем радиусы в точки касания и получим: 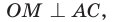
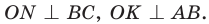
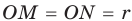
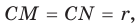
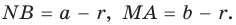
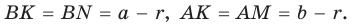
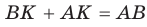
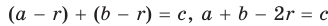
Следствие: 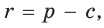
Преобразуем формулу радиуса вписанной окружности:
Формула 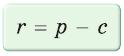
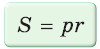
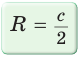
Пример. Дан прямоугольный треугольник, 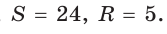
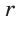
Решение:
Так как 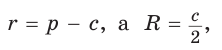
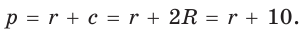
Из формулы 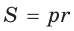
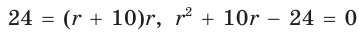
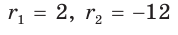
Ответ: 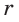
Пример:
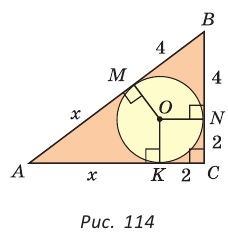
Найти радиус окружности, описанной около прямоугольного треугольника, у которого один из катетов равен 6, а радиус вписанной окружности равен 2.
Решение:
Способ 1 (геометрический). Пусть в треугольнике АВС, где 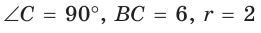
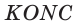
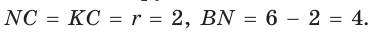
По свойству касательных 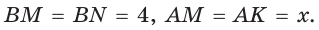
Тогда 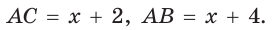
Следовательно, 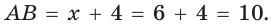
Радиус описанной окружности 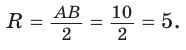
Способ 2 (алгебраический). Подставив в формулу 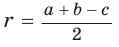
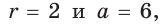
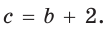
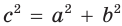
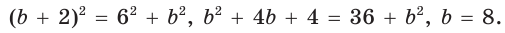
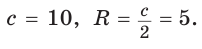
Ответ: 5.
Пример:
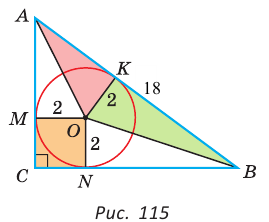
Гипотенуза прямоугольного треугольника 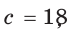
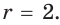
Решение:
Способ 1 (геометрический). Пусть в 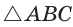
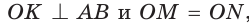
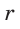
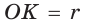
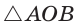
Отсюда 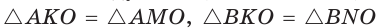
Площадь 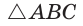
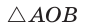
Способ 2 (алгебраический). Из формулы 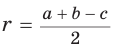
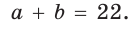
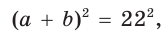
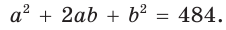
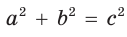
Способ 3 (алгебраический). Из формулы 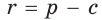
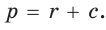
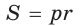
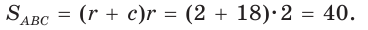
Ответ: 40.
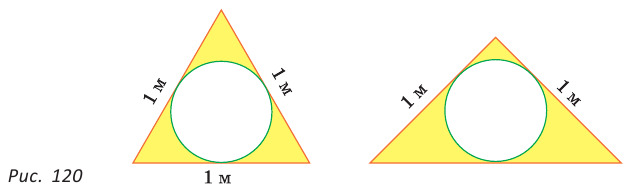
Реальная геометрия:
Есть два листа ДСП (древесно-стружечной плиты). Один из них имеет форму равностороннего треугольника со стороной 1 м, другой — форму прямоугольного равнобедренного треугольника с катетами, равными 1 м (рис. 120). Из каждого листа необходимо вырезать по одному кругу наибольшего диаметра. Определите, из какого листа будет вырезан круг большего диаметра и каким в этом случае будет процент отходов, если известно, что площадь круга можно найти по формуле
Видео:✓ Самая сложная задача в ОГЭ-2020 | Задание 26. Математика | Геометрия | Борис ТрушинСкачать

Вписанные и описанные четырехугольники
Определение. Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность.
Окружность называется вписанной в многоугольник, если она касается всех его сторон. При этом много угольник называется описанным около окружности.
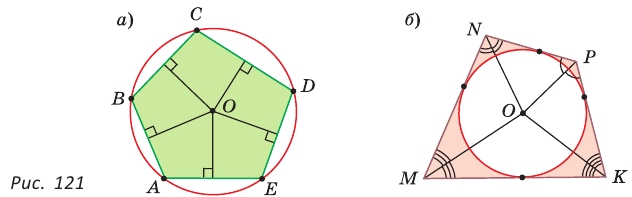
Пятиугольник ABCDE (рис. 121, а) является вписанным в окружность а четырехугольник MNPK (рис. 121, б) — описанным около окружности.
Центр описанной окружности многоугольника находится в точке пересечения серединных перпендикуляров к его сторонам, а центр вписанной — в точке пересечения биссектрис его углов.
Обоснуйте эти утверждения самостоятельно.
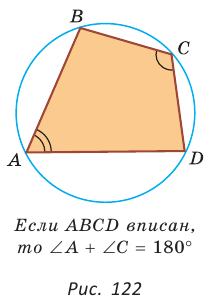
Теорема (свойство вписанного четырехугольника).
Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°.
Пусть ABCD — четырехугольник, вписанный в окружность (рис. 122). Его углы А, В, С и D являются вписанными в окружность. Так как вписанный угол равен половине дуги, на которую он опирается, то 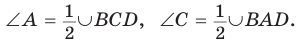
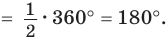
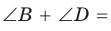
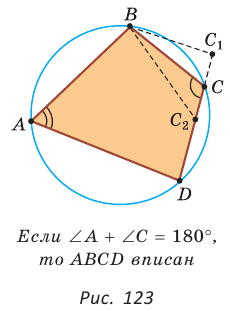
Теорема (признак вписанного четырехугольника).
Если сумма противоположных углов четырехугольника равна 
Рассмотрим четырехугольник ABCD, у которого 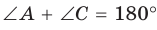
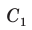
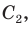
Тогда сумма 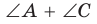
Замечание. Так как сумма углов четырехугольника равна 360°, то для того чтобы около четырехугольника можно было описать окружность, достаточно, чтобы сумма любой пары его противоположных углов была равна 180°.
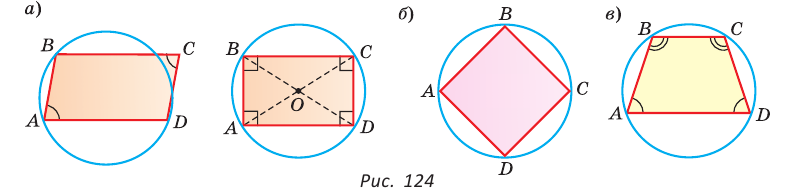
Следствия.
1. Около параллелограмма можно описать окружность, только если этот параллелограмм — прямоугольник (рис. 124, а). Центр этой окружности лежит в точке пересечения диагоналей прямоугольника.
2. Около ромба можно описать окружность, только если этот ромб — квадрат (рис. 124, б).
3. Около трапеции можно описать окружность, только если она равнобедренная (рис. 124, в).
Докажите эти следствия самостоятельно.
Теорема (свойство описанного четырехугольника ).
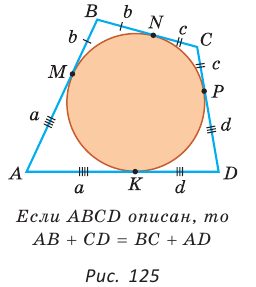
Суммы противоположных сторон описанного четырехугольника равны между собой.
Пусть ABCD — описанный четырехугольник, М, N, Р и К — точки касания его сторон с окружностью (рис. 125). Так как отрезки касательных, проведенных к окружности из одной точки, равны между собой, то AM = АК = а, ВМ = BN = b, СР = CN = с, DP = DK = d. Тогда
откуда AD + ВС = AB + CD.
Теорема доказана.
Следствие:
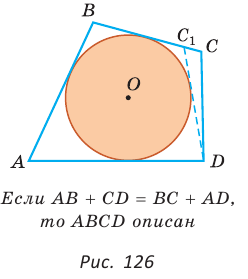
Периметр описанного четырехугольника равен удвоенной сумме длин любой пары его противоположных сторон:
Теорема (признак описанного четырехугольника).
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Пусть для выпуклого четырехугольника ABCD справедливо, что
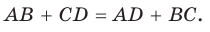
Проведем окружность, которая касается прямых AD, АВ и ВС (рис. 126). Такая окружность существует, ее центр находится в точке пересечения биссектрис углов А и В. Если окружность не касается стороны CD, то либо прямая CD не имеет с окружностью общих точек, либо является секущей. Рассмотрим первый случай. Проведем отрезок 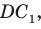
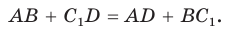
Отняв почленно от равенства (1) равенство (2), получим 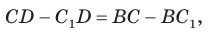
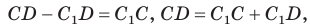
Рассмотрев случай, когда прямая DC — секущая, также придем к противоречию (сделайте это самостоятельно). Следовательно, данная окружность касается стороны CD и в четырехугольник ABCD можно вписать окружность. Теорема доказана.
Следствия.
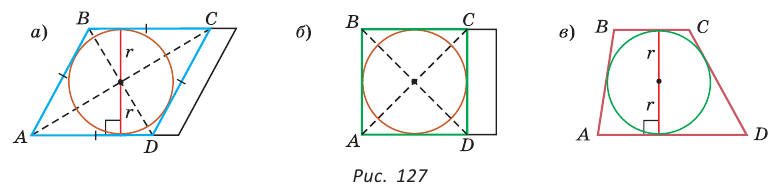
1. В параллелограмм можно вписать окружность, только если этот параллелограмм — ромб. Центр этой окружности лежит в точке пересечения диагоналей ромба, а ее диаметр равен высоте ромба (рис. 127, а).
2. В прямоугольник можно вписать окружность, только если этот прямоугольник — квадрат (рис. 127, б).
3. Диаметр окружности, вписанной в трапецию, равен ее высоте (рис. 127, в).
Докажите эти следствия самостоятельно.
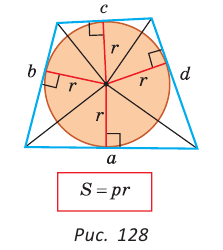
Для описанного многоугольника справедлива формула 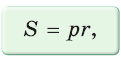
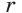
Доказательство аналогично приведенному в § 8 для треугольника. Выполните его самостоятельно, используя рисунок 128.
Пример:
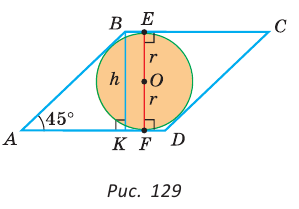
Найти радиус окружности, вписанной в ромб с периметром 24 см и острым углом, равным 45°.
Решение:
Способ 1 (решение прямоугольного треугольника). Пусть ABCD — ромб (рис. 129), О — центр вписанной в ромб окружности. Известно, что высота ВК ромба равна диаметру EF вписанной окружности, т. е. 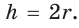
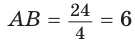
Из прямоугольного треугольника АВК находим. что 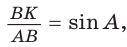
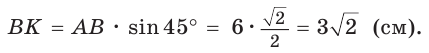
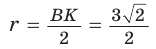
Способ 2 (метод площадей). Ромб — параллелограмм. По формуле площади параллелограмма 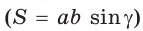
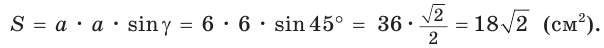
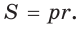
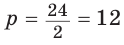
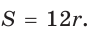
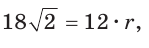
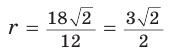
Ответ: 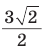
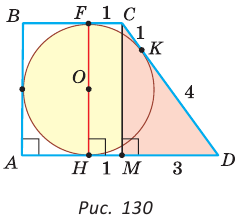
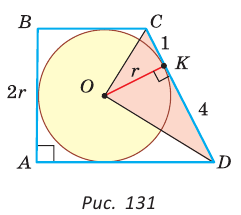
Пример:
Окружность, вписанная в прямоугольную трапецию ABCD, где 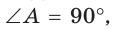
Решение:
Способ 1. Площадь трапеции находится по формуле 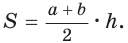
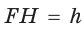
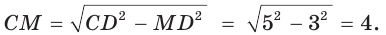
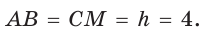
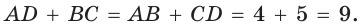
Способ 2*. Центр О вписанной окружности лежит на пересечении биссектрис углов 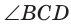
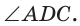
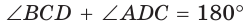
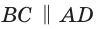
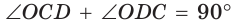
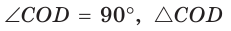
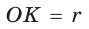
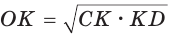
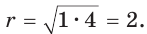
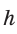
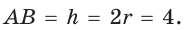
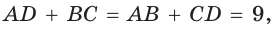
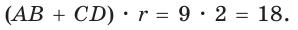
Ответ: 18.
Замечание. Полезно запомнить свойство: «Боковая сторона описанной трапеции видна из центра вписанной окружности под углом 90°».
Пример:
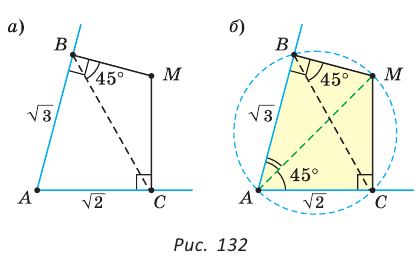
Внутри острого угла А взята точка М, из которой опущены перпендикуляры МВ и МС на стороны угла А, 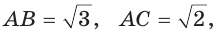
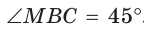
Решение:
Так как в четырехугольнике АВМС сумма углов В и С равна 180°, то около него можно описать окружность. Проведем в ней хорду AM (рис. 132, б). Поскольку 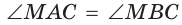
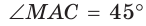
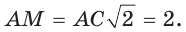
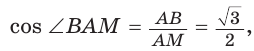
Окружность, вписанная в треугольник
Пример:
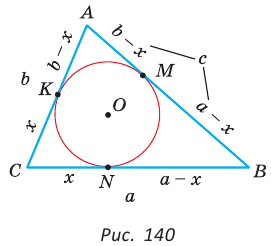
Окружность вписана в треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с. Вывести формулу для нахождения длин отрезков, на которые точки касания окружности со сторонами делят каждую сторону треугольника.
Решение:
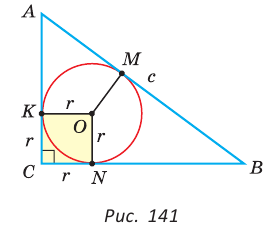
Пусть К, М и N — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника АВС (рис. 140). Известно, что отрезки касательных, проведенных из одной точки к окружности, равны между собой.
Тогда, если 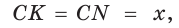
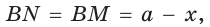
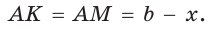
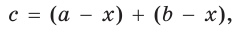
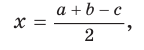
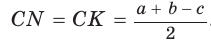
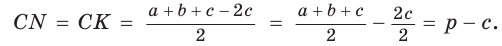
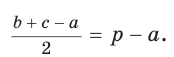
Ответ:
Замечание. Если 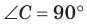
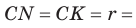
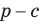
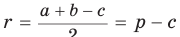
Описанная трапеция
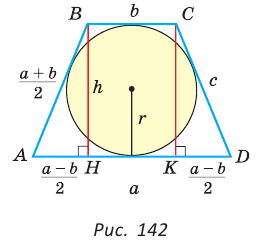
Пример:
Найти площадь описанной равнобедренной трапеции с основаниями а и Ь.
Решение:
Площадь трапеции можно найти по формуле 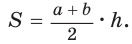
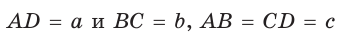
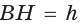
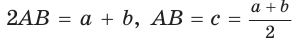
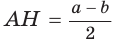
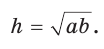
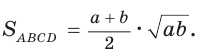
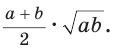
Замечание. Площадь описанной равнобедренной трапеции равна произведению среднего арифметического и среднего геометрического ее оснований.
Полезно запомнить!
Для описанной равнобедренной трапеции с основаниями 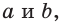
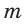
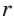
Дополнительные свойства и признаки вписанного четырехугольника
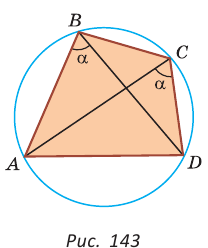
Теорема.
Около четырехугольника можно описать окружность тогда и только тогда, когда угол между его стороной и диагональю равен углу между противоположной стороной и другой диагональю.
Рис. 143
1. Если четырехугольник ABCD вписан в окружность (рис. 143), то 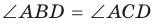
2. Докажем, что если в некотором четырехугольнике ABCD 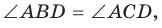
Опишем около треугольника ABD окружность.
В 8-м классе (В. В. Казаков. «Геометрия, 8», с. 186) было доказано свойство:
«Геометрическим местом точек плоскости, из которых данный отрезок AD виден под углом а, является объединение двух дуг окружностей: дуги ABD и ей симметричной относительно прямой AD, исключая точки 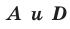
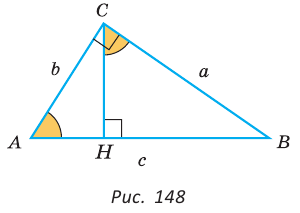
Обобщенная теорема Пифагора
В прямоугольном треугольнике 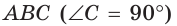
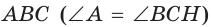
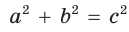
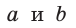
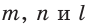
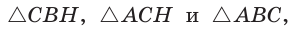
Действительно, из подобия указанных треугольников 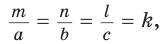
Пример:
Пусть 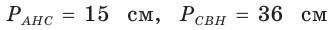
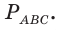
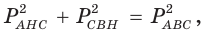
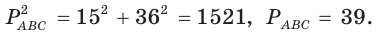
Ответ: 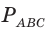
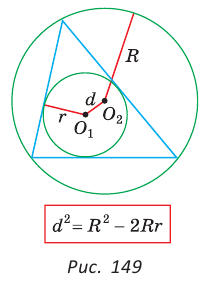
Формула Эйлера для окружностей
Для вписанной и описанной окружностей треугольника с радиусами 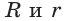
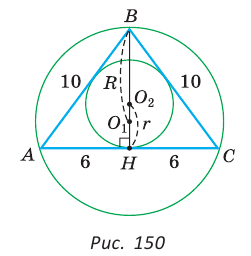
Проверим справедливость этой формулы на примере равнобедренного треугольника АВС, у которого АВ = ВС = 10, АС = 12 (рис. 150).
Вначале найдем расстояние между центрами указанных окружностей традиционным способом.
Проведем высоту ВН, длина которой будет равна 8 (пифагорова тройка 6, 8, 10). Центры описанной и вписанной окружностей — соответственно точки 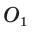
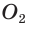
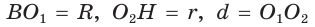
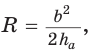
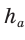
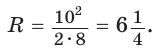
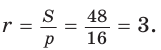
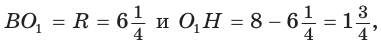
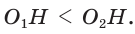
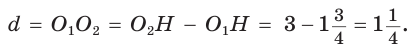
А теперь найдем d по формуле Эйлера:
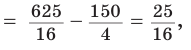
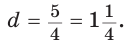
Запомнить:
- Центр описанной окружности треугольника (многоугольника) лежит в точке пересечения серединных перпендикуляров к его сторонам.
- Центр вписанной окружности треугольника (многоугольника) лежит в точке пересечения биссектрис его углов.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, а ее радиус равен половине гипотенузы:
- Радиус вписанной окружности прямоугольного треугольника находится по формуле
- Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°. И обратно.
- Если четырехугольник описан около окружности, то суммы его противоположных сторон равны между собой. И обратно.
- Площадь треугольника и описанного многоугольника можно найти по формуле
где
— полупериметр,
— радиус вписанной окружности.
Справочная информация по описанной и вписанной окружности треугольника
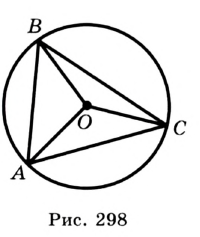
Определение. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.
На рисунке 298 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность. Очевидно, что центр описанной окружности треугольника равноудален от всех его вершин. На рисунке 298 точка 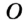
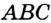
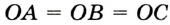
Теорема 21.1. Вокруг любого треугольника можно описать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 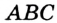
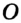
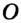
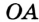
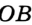
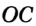
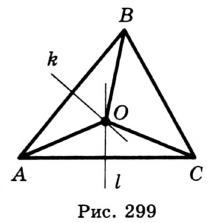
На рисунке 299 изображен произвольный треугольник 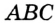
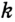
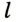
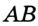
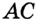
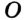

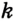
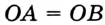
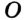
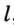
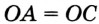
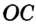

Заметим, что вокруг треугольника можно описать только одну окружность. Это следует из того, что серединные перпендикуляры 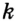
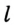
Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Следствие 2. Центр описанной окружности треугольника — это точка пересечения серединных перпендикуляров его сторон.
Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон.
На рисунке 300 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
Точка 
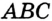
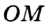
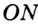
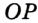
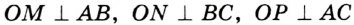
Теорема 21.2. В любой треугольник можно вписать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 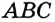
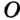
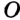
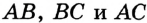
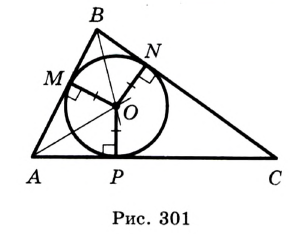
На рисунке 301 изображен произвольный треугольник 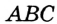


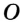





Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов 

Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке.
Следствие 2. Центр вписанной окружности треугольника — это точка пересечения его биссектрис.
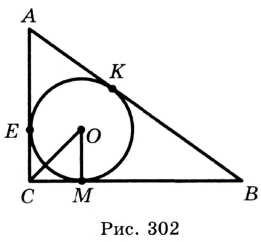
Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле 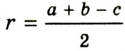
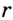
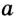
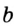
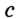
Решение:
В треугольнике 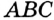
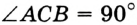
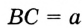
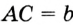
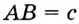
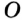
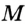
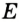
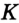
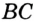
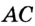
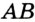
Отрезок 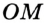
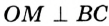
Так как точка 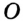
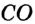
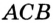
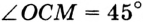
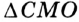
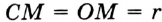
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Первый признак равенства треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔥 Видео
Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Центр вписанной окружности #ShortsСкачать

Точка O – центр окружности, ∠BOC=160° ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

ОГЭ ЗАДАНИЕ 16 ТОЧКА О ЦЕНТР ОКРУЖНОСТИ, НА КОТОРОЙ ЛЕЖАТ ТОЧКИ А В И ССкачать
Где искать центр описанной окружности #геометрия #огэ #егэ #математикаСкачать

Точка O центр окружности описанной около остроугольного треугольникаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Разбор Задачи №16 из Варианта Ларина №271Скачать

Радиус описанной окружностиСкачать








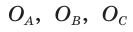
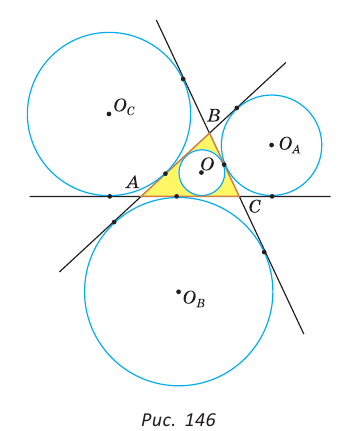
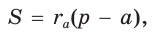
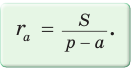
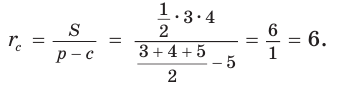
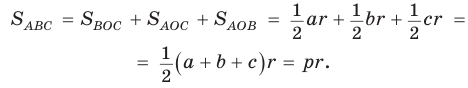
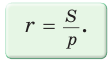
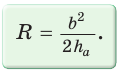
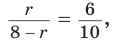
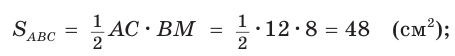
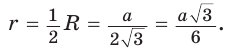
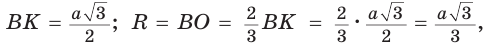
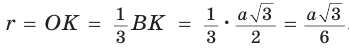
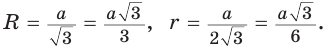
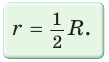
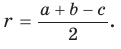
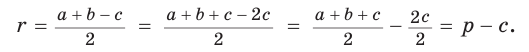
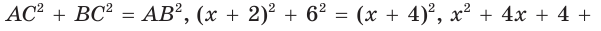
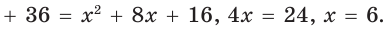
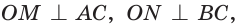
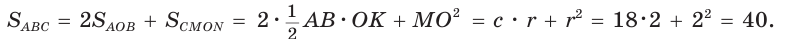
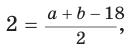
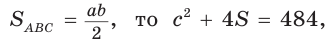
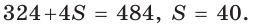
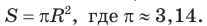

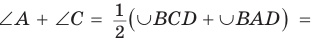
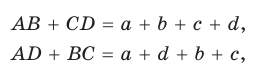
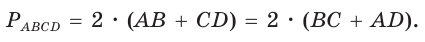
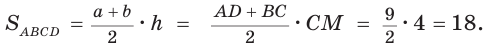
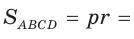
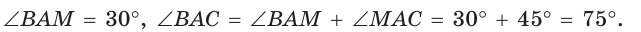
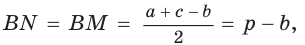
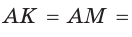
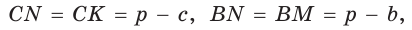
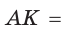
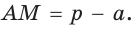
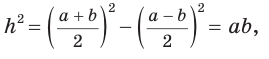
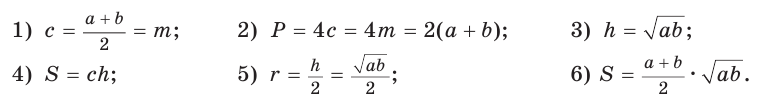
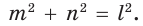
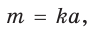
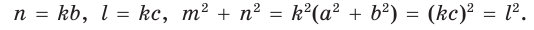
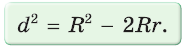
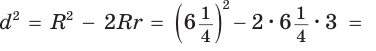
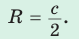
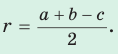
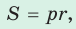 где
где 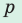 — полупериметр,
— полупериметр, 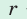 — радиус вписанной окружности.
— радиус вписанной окружности.