Нити изогнутой по дуге окружности радиусом 10 см (6 видео)

По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределён заряд q = 20 нКл. Используя принцип суперпозиции, определите напряжённость электростатического поля E

Готовое решение: Заказ №8798

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 29.09.2020

Цена: 209 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Содержание

Описание и исходные данные задания, 50% решения + фотография:
Электронная библиотека
Нити изогнутой по дуге окружности радиусом
Нити изогнутой по дуге окружности радиусом
По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределён заряд q = 20 нКл. Используя принцип суперпозиции, определите напряжённость электростатического поля E
Описание и исходные данные задания, 50% решения + фотография:
1001. Точка обращается по окружности радиусом
📸 Видео

Описание и исходные данные задания, 50% решения + фотография:

№2 321. По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределён заряд q = 20 нКл. Используя принцип суперпозиции, определите напряжённость электростатического поля E, создаваемого этим зарядом в центре кривизны дуги, если длина нити равна четверти длины окружности.

Решение.

Четверть кольца радиуса имеет длину:

Определим линейную плотность заряда:

Рассмотрим элементарный участок четверти кольца.

Если вам нужно решить физику, тогда нажмите ➔ помощь по физике.

Похожие готовые решения:

Цепь состоит из катушки индуктивностью L = 0,1 Гн и источника тока. Источник тока отключили, не разрывая цепи. Время, через которое сила тока уменьшится до 0,001 первоначального значения
Поверхностная плотность заряда бесконечно протяжённой вертикальной плоскости равна 400 мкКл/м2. К плоскости на нити подвешен заряженный тяжёлый шарик массой m = 10 г. Определить заряд Q
Бесконечный тонкий прямой проводник равномерно заряжен с линейной плотностью заряда = 5•10-10 Кл/м. Считая, что на расстоянии r1 = 1 м от проводника потенциал созданного им электрического поля
Четверть тонкого кольца радиусом R = 10 см несёт равномерно распределённый заряд Q = 0,05 мкКл. Определить напряжённость E электрического поля, создаваемого распределённым зарядом в точке

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Радиус и диаметрСкачать

Электронная библиотека

Пример 1. Расстояние (l) между двумя точечными зарядами Q₁ = 2 нКл и Q₂ = -3 нКл, расположенными в вакууме, равно 20 см. Определить: 1) напряженность ( ); 2) потенциал (j) поля, создаваемыми этими зарядами в точке, удаленной от первого заряда на расстоянии r₁ = 15 см и от второго заряда на r₂ = 10 см.

Определить: 1) ; 2) j.

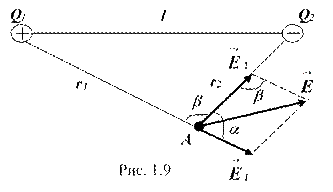
Решение. Согласно принципу суперпозиции имеем: (рис.1.9).

Напряженности электрического поля, создаваемые в вакууме зарядами Q₁ и Q₂ , равна:

Модуль вектора находится по теореме косинусов:

Подставив (1) и (3) в формулу (2), найдем искомую напряженность в точке А:

Согласно принципу суперпозиции, потенциал результирующего поля:

где и – соответственно потенциалы полей, создаваемых зарядами Q₁ и Q₂.

Подставив последние выражения в (4), найдем:

Вычисляя, получим: 1) = 3 кВ/м; 2) j = -150 В.

Пример 2. Электрическое поле создается бесконечно длинным цилиндром радиусом R = 7 мм, равномерно заряженным с линейной плотностью t = 15 нКл/м. Определить: 1) напряженность ( ) поля в точках, лежащих от оси цилиндра на расстояниях r₁ = 5 мм и r₂ = 1 см; 2) разность потенциалов между двумя точками этого поля, лежащими на расстоянии r₃ = 1 см и r₄ = 2 см от поверхности цилиндра, в средней его части.

Определить: 1) , ; 2) .

Решение. Воспользуемся теоремой Гаусса (1.1):

взяв в качестве замкнутой поверхности цилиндр, коаксиальный с заряженным, радиусом r и высотой l (рис. 1.10). Если r R

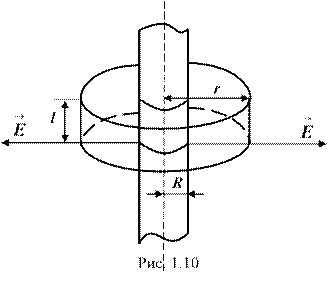
Так как , то полученная формула для поля с осевой симметрией запишется в виде:

Подставив сюда выражение для напряженности поля, создаваемого бесконечно длинным цилиндром , получим:

Проинтегрировав это выражение, найдем искомую разность потенциалов:

Вычисляя, получим: 1) = 0; = 27 кВ/м; 2) = 125 В.

Пример 3. Две концентрические проводящие сферы радиусами R₁ = 6 см и R₂ = 10 см несут соответственно заряды Q₁ = 1 нКл и Q₂ = -0,5 нКл. Найти напряженность ( ) поля в точках, находящихся от центра сфер на расстояниях: r₁ = 5 см, r₂ = 9 см, r₃ = 15 см. Построить график .

Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 1.11): области I , области II , области III .

1) Для определения напряженности ( ) в области I проведем гауссову поверхность S₁ радиусом r₁ и воспользуемся теоремой Гаусса:

так как суммарный заряд, находящийся внутри гауссовой поверхности, равен нулю. Из соображений симметрии имеем: . Следовательно, и (напряженность поля в области I) во всех точках, удовлетворяющих условию , будет равна нулю.

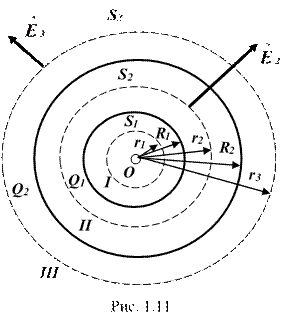
2) В области II гауссову поверхность проведем радиусом r₂.

так как внутри гауссовой поверхности находится только заряд Q₁.

Так как , то можно вынести за знак интеграла:

Обозначив напряженность для области II через , получим:

где – площадь гауссовой поверхности.

1) В области III гауссова поверхность проводится радиусом r₃. Обозначим напряженность области III через и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен: . Тогда

Заметим, что ,поэтому это выражение можно переписать в виде:

Убедимся в том, что первая часть равенств (1) и (2) дает единицу напряженности:

Вычисляя, получим: = 0; = 1,11 кВ/м; = 200 В/м.

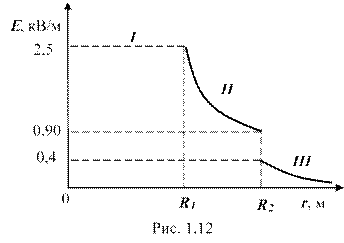
2) Построим график (рис. 1.12).

В области II изменяется по закону . В точке напряженность равна:

В области III изменяется по закону , причем в точке (r стремится к R₂ справа) и напряжённость равна: = 0,45 кВ/м.

Таким образом, функция в точках и терпит разрыв.

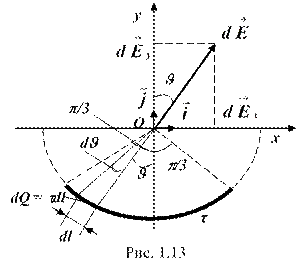
Пример 4. По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью t = 10 нКл/м. Определить напряженность ( ) и потенциал (j) электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина (l) нити составляет 1/3 длины окружности и равна 15 см.

Дано: t = 10 нКл/м = 10×10 -9 Кл;

Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Oy была симметрично расположена относительно концов дуги (рис. 1.13). На нити выделим элемент длины dl. Заряд dQ = tdl, находящийся на выделенном участке, можно считать точечным.

Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность ( ) поля, создаваемого зарядом dQ:

где r – модуль радиуса-вектора, направленного от элемента dl к точке, в которой вычисляется напряженность.

Выразим вектор через проекции и на оси координат:

где и – единичные векторы направлений (орты).

Напряженность найдем интегрированием:

Интегрирование ведется вдоль дуги длиной l. В силу симметрии . Тогда

где . Так как , , то

Подставим выражение в (1) и, приняв во внимание симметричное расположение дуги относительно оси Oy, пределы интегрирования возьмем от 0 до p/3, а результат удвоим:

Из этой формулы видно, что напряженность поля по направлению совпадает с осью Oy.

Найдем потенциал электрического поля в точке О. Сначала найдем потенциал (dj), создаваемый точечным зарядом dQ в точке О:

Заменим r на R и проведем интегрирование:

Вычисляя, получим: = 2,18 кВ/м; j = 188 В.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Видео:Длина окружности. Математика 6 класс.Скачать

Нити изогнутой по дуге окружности радиусом

Видео:Центростремительное ускорение. 9 класс.Скачать

Нити изогнутой по дуге окружности радиусом

2018-04-03
Проволока изогнута по дуге окружности радиуса $R = 0,5 м$. По проволоке без трения может двигаться кольцо. Какую скорость надо сообщить кольцу, находящемуся в точке О, чтобы оно, слетев с окружности в точке А, попало на проволоку в точке В. Угол равен $alpha = 60^ $. Ускорение свободного падения считать равным $g = 10 м/с^ $.

Из закона сохранения энергии $mgh + frac > = frac ^ > $. Высота $h = (R + R cos alpha)$
Расстояние между точками А и В равно $S = frac 2 sin alpha cos alpha > = 2R sin alpha$, следовательно $V^ = frac $. Подставляем эти величины в закон сохранения энергии

$mgR(1 + cos alpha) + frac = frac ^ > Rightarrow V_ ^ = frac + 2gR(1 + cos alpha) = 5gR$, т.к $cos alpha = frac , alpha = 60^ $.
$V_ = sqrt = 5 м/с$
Ответ: 5м/с

Видео:Окружность. Как найти Радиус и ДиаметрСкачать

По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределён заряд q = 20 нКл. Используя принцип суперпозиции, определите напряжённость электростатического поля E

Готовое решение: Заказ №8798

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 29.09.2020

Цена: 209 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Описание и исходные данные задания, 50% решения + фотография:

Решение.

Четверть кольца радиуса имеет длину:

Определим линейную плотность заряда:

Рассмотрим элементарный участок четверти кольца.

Если вам нужно решить физику, тогда нажмите ➔ помощь по физике.

Похожие готовые решения:

Цепь состоит из катушки индуктивностью L = 0,1 Гн и источника тока. Источник тока отключили, не разрывая цепи. Время, через которое сила тока уменьшится до 0,001 первоначального значения
Поверхностная плотность заряда бесконечно протяжённой вертикальной плоскости равна 400 мкКл/м2. К плоскости на нити подвешен заряженный тяжёлый шарик массой m = 10 г. Определить заряд Q
Бесконечный тонкий прямой проводник равномерно заряжен с линейной плотностью заряда = 5•10-10 Кл/м. Считая, что на расстоянии r1 = 1 м от проводника потенциал созданного им электрического поля
Четверть тонкого кольца радиусом R = 10 см несёт равномерно распределённый заряд Q = 0,05 мкКл. Определить напряжённость E электрического поля, создаваемого распределённым зарядом в точке

Присылайте задания в любое время дня и ночи в ➔

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

1001. Точка обращается по окружности радиусом

Название	1001. Точка обращается по окружности радиусом
Анкор	fizika
Дата	14.12.2021
Размер	1.8 Mb.
Формат файла
Имя файла	Chast_1_dlya_2.doc
Тип	Документы #303206
страница	9 из 10

Подборка по базе: 2 точка задача (1) (2).doc, Зимний кроссворд_Соедини по точкам.pdf, Контрольная точка №1. Философия.docx, Пример c точками.docx, 3 точка copy.docx, 2 точка задача (1) (2).doc, Контрольная точка № 2. Собеседование. Резюме.docx, Контрольная точка немецкий язык.docx, 1-я точка 2105 .docx, 1 контрольная точка.docx

ℓ = 20 см, стоящая на гладкой горизонтальной поверхности, начинает падать из вертикального положения. Определить скорость верхнего конца спицы перед уларом его о поверхность.

1222. Давление р ветра на стену равно 200 Па. Определить скорость υ ветра, если он дует перпендикулярно стене. Плотность ρ воздуха равна 1,29 кг/м 3 .

1255. Определите, при каком радиусе орбиты R _сп спутник может двигаться в плоскости экватора так, чтобы все время находиться над одной и той же точкой поверхности Земли. Считать известными ускорение g свободного падения у поверхности Земли и ее радиус R .

1296. Цилиндр массой 0,1 кг с площадью основания 10 см 2 плавает в вертикальном положении в жидкости с плотностью 1000 кг / м 3 и вязкостью 0,001 Па∙с. Его погрузили ещё немного и отпустили. Вывести уравнение колебаний.

2028. Сухой воздух состоит в основном из кислорода и азота. Если пренебречь остальными составными частями воздуха, то можно считать, что массовые доли кислорода и азота соответственно  ₁ = 0,232,  ₂ = 0,768. Определить относительную молекулярную массу М _r воздуха.

2063. Найти среднюю квадратичную  _кв > среднюю арифметическую  > и наиболее вероятную  _в скорости молекул водорода. Вычисления выполнить для трех значений температуры: 1) T = 20 К; 2) T = 300 К; 3) Т = 5 кК.

2097. Найти среднюю длину пробега молекулы азота в сосуде с объемом V = 5 л. Масса газа m = 0,5 г.

2128. На сколько ньютонов уменьшится вес акваланга с баллонами объёмом 16,6 л , если давление воздуха в баллонах упадёт со 150 до 60 атмосфер? Молярная масса воздуха равна 0,029 кг / моль , а температура – 300 К . Одна атмосфера равна 100 кПа .

2162. Определить в процентах КПД газовой горелки, если в ней используется газ, удельная теплота сгорания которого 36 МДж / м 3 , а на нагревание чайника с 3 кг воды от 10 ºС до кипения было израсходовано 60 л газа. Теплоёмкость чайника 2,4 кДж / К , удельная теплоёмкость воды 4,2 кДж /( кг·К ), плотность газа – 1 кг / м 3 .

2196. Определить поверхностное натяжение масла, плотность которого 0,91 г / см 3 , если при пропускании через пипетку 4 см 3 масла получено 304 капли. Диаметр шейки пипетки 1,2 мм .

3028. По тонкой нити, изогнутой по дуге окружности радиуса R = 10 см, равномерно распределен заряд Q = 20 нКл. Определить напряженность E поля, создаваемого этим зарядом в точке, совпадающей c центром кривизны дуги, если длина нити равна четверти длины окружности.

3063. Бесконечная плоскость заряжена отрицательно с поверхностной плотностью σ = 35,4 нКл / м 2 . По направлению силовой линии поля, созданного плоскостью, летит электрон. Определить минимальное расстояние, на которое может подойти к плоскости электрон, если на расстоянии ℓ ₀ = 5 см он имел кинетическую энергию Т = 80 эВ .

3097. Расстояние между пластинами плоского воздушного конденсатора, присоединенного к источнику напряжения с ЭДС 180 В равно 5 мм . Площадь пластин конденсатора 175 см 2 . Найти работу по раздвижению пластин до расстояния 12 мм в двух случаях; 1) конденсатор перед раздвижением пластин отключен от источника; 2) конденсатор в процессе раздвижения пластин все время соединен с источником.

3128. Три сопротивления r ₁ = 12 Ом, r ₂ = 4 Ом, r ₃ = 10 Ом соединены параллельно. Общий ток в цепи I = 0,3 А. Найти силу тока, идущего через сопротивление r ₃ .

3162. Сила тока в проводнике равномерно увеличивается от нуля до некоторого максимального значения в течение времени t = 20 c. За это время в проводнике выделилась теплота Q = 4 кДж. Определить скорость нарастания тока в проводнике, если сопротивление его R = 5 Ом.

3196. Найти силу тока насыщения между пластинами конденсатора, если под действием ионизатора в каждом кубическом сантиметре пространства между пластинами конденсатора ежесекундно образуется n ₀ = 10 8 пар ионов, каждый из которых несет один элементарный заряд. Расстояние d между пластинами конденсатора равно 1 см , площадь S пластины равна 100 см 2 .

Вариант 22
1036. Камень бросают горизонтально с горы, уклон которой равен  = 15º. Определить, с какой скоростью  ₀ был брошен камень, если он упал на склон на расстоянии ℓ = 20 м от точки бросания.

1074. Медный шар радиусом R = 10 см вращается с частотой ν = 2 Гц вокруг оси, проходящей через его центр. Плотность меди 8,6∙10 3 кг/м 3 . Какую работу нужно совершить, чтобы увеличить его угловую скорость вдвое?

1112. Медная проволока диаметром 1 мм разрывается при нагрузке 188,4 Н. Найти предел прочности меди при растяжении.

1149. Пуля массой m = 12 г , летящая с горизонтальной скоростью υ = 0,6 км / с , попадает в мешок с песком массой M = 10 кг , висящий на длинной нити, и застревает в нем. Определить: 1) высоту, на которую поднимется мешок, отклонившись после удара, 2) долю кинетической энергии, израсходованной на пробивание песка.

1186. На гладком полу стоит сосуд, заполненный водой плотности ρ ₀ = 10 3 кг/м 3 , объем воды V ₀ = 10 л. Оказавшейся на дне сосуда жук объема V = 9 см 3 и плотности ρ = 2∙10 3 кг/м 3 через некоторое время начинает ползти по дну сосуда со скоростью u = 2 см/с относительно него. С какой скоростью станет двигаться сосуд по полу? Массой сосуда пренебречь, уровень воды всё время остается горизонтальным.

1223. Струя воды с площадью S ₁ поперечного сечения, равной 4 см 2 , вытекает в горизонтальном направлении из брандспойта, расположенного на высоте H = 2 м над поверхностью Земли, и падает на эту поверхность на расстоянии ℓ = 8 м. Пренебрегая сопротивлением воздуха движению воды, найти избыточное давление p воды в рукаве, если площадь S ₂ , поперечного сечения рукава равна 50 см 2 ?

1260. Определить максимальное ускорение а _max материальной точки, совершающей гармонические колебания c амплитудой A = 15 см, если наибольшая скорость точки υ _max = 30 см/с. Написать также уравнение колебаний.

1297. На гладком горизонтальном столе лежит шар массой 280 г , прикрепленный к легкой горизонтально расположенной пружине с жесткостью 500 Н / м . В шар попадает пуля массой 8 г , летящая горизонтально со скоростью 300 м / с , и застревает в нём. Коэффициент трения шара о стол равен 0,1. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, вывести уравнение колебаний шара.

2029. В сосуде вместимостью V = 15 л находится смесь азота и водорода при температуре t = 23 °С и давлении р = 200 кПа. Определить массы смеси и ее компонентов, если массовая доля  ₁ азота в смеси равна 0,7.

2064. Колба вместимостью V =4 л содержит некоторый газ массой m = 0,6 г под давлением p = 200 кПа. Определить среднюю квадратичную скорость _кв > молекул газа.

2098. Водород находится под давлением р = 20 мкПа и имеет температуру Т = 300 К. Определить среднюю длину свободного пробега молекулы такого газа.

2129. Давление воздуха внутри бутылки равно 0,1 МПа при температуре 7 ºС. До какой температуры надо нагреть бутылку, чтобы из неё вылетела пробка? Пробку можно вынуть силой 10 Н. Поперечное сечение пробки имеет площадь 2 см 2 . Атмосферное давление 100 кПа .

2163. Мощность двигателя автомобиля при скорости 20 м / с равна 40 кВт . Определить расход бензина на 100 км пути при этой скорости, если КПД двигателя равен 50%. Удельная теплота сгорания бензина равна 5·10 7 Дж / кг .

2197. Какую массу имеет капля воды, вытекающая из стеклянной трубки диаметром 1 мм ? Считать диаметр капли равным диаметру шейки трубки.

3029. Определить напряженность E поля, создаваемого зарядом, равномерно распределенным по тонкому прямому стержню c линейной плотностью заряда τ = 200 нКл/м, в точке, лежащей на продолжении оси стержня на расстоянии а = 20 см от ближайшего конца. Длина стержня ℓ = 40 см.

3064. Найти силу F электростатического отталкивания между ядром атома натрия и бомбардирующим его протоном, считая, что протон подошел к ядру атома натрия на расстояние r = 6·10 –14 м. Заряд ядра натрия в 11 раз больше заряда протона. Влиянием электронной оболочки пренебречь.

3098. Пластины плоского конденсатора площадью S = 0,01 м 2 каждая притягиваются друг к другу с силой F = 30 нН . Пространство между пластинами заполнено слюдой (ε = 7). Найти заряды q , находящихся на пластинах, напряжённость Е поля между пластинами и объёмную плотность энергии ω поля.

3129. Цепь, имеющая сопротивление 100 Ом , питается от источника постоянного напряжения. Амперметр с внутренним сопротивлением 1 Ом , включенный в цепь, показал силу тока 5 А . Какова была сила тока в цепи до включения амперметра?

3163. Сила тока в проводнике меняется со временем по закону I = I ₀ e -αt . Начальная сила тока I ₀ = 20 A,  = 10 2 c -1 . Определить теплоту, выделившуюся в проводнике за время t = 10 -2 с.

3197. К электродам разрядной трубки, содержащей водород, приложена разность потенциалов U = 10 В. Расстояние ℓ между электродами равно 25 см. Ионизатор создает объем V = 1 см 3 водорода n = 10 7 пар ионов в секунду. Найти плотность тока j в трубке. Определить также, какая часть силы тока создается движением положительных ионов.

Вариант 23
1037. На каком расстоянии от трубы ТЭЦ-2 города Волжского упадет камень, брошенный горизонтально с верхнего балкона этой трубы ( H = 82 м), если в момент броска скорость камня 20 м/с. Найти время полета камня.

1075. Сплошной шар скатывается с наклонной плоскости за 3 с. За сколько времени скатится другой сплошной шар, радиус которого в 2 раза меньше, с той же наклонной плоскости? Материал шаров одинаковый.

1113. Железная проволока при 30 ºС натянута горизонтально и закреплена концами между неподвижными опорами. С какой силой будет действовать проволока на точки закрепления при понижении температуры до –10 ºС. Площадь сечения проволоки 2 мм 2 .

1150. Шар катится по горизонтальной поверхности со скоростью υ = 1.5 м / с . На какое расстояние ℓ вкатится он на наклонную плоскость с углом наклона α = 10º?

1187. В цилиндрический сосуд налиты равные массы ртути и воды. Общая высота двух слоев жидкостей 29,2 см. Определить давление жидкостей на дно сосуда.

1224. Бак высотой Н = 2 м до краев заполнен жидкостью. На какой высоте h должно быть проделано отверстие в стенке бака, чтобы место падения струи, вытекающей из отверстия, было на максимальном от бака расстоянии?

1261. Точка совершает гармонические колебания, уравнение которых