- Трибар
- Тройной деформированный трибар
- Треугольник из 12 кубов
- Крылатый трибар
- Тройное домино
- Кубик со штифтами
- Усеченный трибар
- Перекрещенный ромб
- Головоломка из кубиков
- Усеченный деформированный трибар
- Летучий шестиугольник
- Прямоугольный триэдр (трехгранник)
- Методические материалы проекта «Удивительные треугольники»
- Выберите документ из архива для просмотра:
- Описание презентации по отдельным слайдам:
- Треугольники в жизни человека
- Скачать:
- Подписи к слайдам:
- Предварительный просмотр:
- 📽️ Видео
Видео:Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

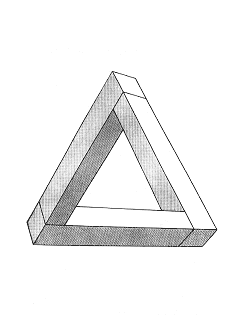
Трибар
Эта фигура возможно, первый опубликованный в печати невозможный объект. Она появилась в 1958 году в журнале British Journal of Psychology, в статье под заголовком «Удивительные фигуры, особый вид оптических иллюзий». Ее авторы, отец и сын Лайонелл и Роджер Пенроузы, генетик и математик соответственно, определили этот объект как «трехмерную прямоугольную структуру». Она также получила название «трибар», или «деформированный трибар». В этой статье фигурировали еще два загадочных объекта. Таким образом, «невозможные объекты» были впервые представлены широкой общественности на примере этих трех фигур.
Вскоре Мауриц К. Эшер (1898 1972), ныне очень популярный голландский художник-сюрреалист, открыл для себя треугольник Пенроуза. В то время он только начал увлекаться конструированием нереальных миров. Впоследствии треугольник Пенроуза, или трибар, вдохновил Эшера на создание литографии «Водопад» (1961), которая пользовалась огромным успехом. В этой литографии художник остроумно объединил три трибара. Эшер создал, в сущности, визуально убедительную конструкцию с вечным двигателем. Она является вечной, поскольку обеспечивает непрерывный поток воды по всей окружности, которая образована тремя соединенными между собой треугольниками. Любой, кто был в магазине, где продаются книги и плакаты, мог видеть эту картину. Не только Эшер, но и многие другие художники, основываясь на предыдущих работах, копировали трибар и перепечатывали его в измененном виде. Среди 4 типов невозможных объектов трибар является первым. За ним следуют «Бесконечная лестница», «Космическая вилка» и «Сумасшедший ящик».
С первого взгляда трибар кажется просто изображением равностороннего треугольника. Однако, рассмотрев его получше, мы понимаем, что в нем есть что-то странное. Стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В то же время левая и правая грани внизу тоже кажутся перпендикулярными. Вы смотрите на каждый угол треугольника под разным углом зрения. Если рассматривать отдельные части этого треугольника, как бы он ни назывался, то их еще можно считать реальными, но в общем эта фигура не может существовать в действительности. Она не деформирована, но при черчении были неправильно соединены правильные элементы.
Видео:Эта Находка в Бермудском Треугольнике Испугала Всех УченыхСкачать

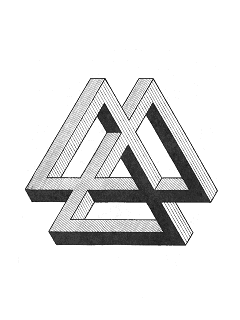
Тройной деформированный трибар
Фигура справа это простая, но более глубокая разработка треугольника Пенроуза. На примере первого трибара можно было увидеть лишь одно невозможное соединение, а в этой фигуре несколько. Вы на каждом шагу начинаете по-новому смотреть на нее так получается с любым невозможным объектом. Предмет кажется довольно убедительным, но если вы попробуете построить что-то подобное в реальности, то у вас ничего не выйдет. Вот в чем суть всех невозможных объектов!
Видео:100 Фактов о Бермудском Треугольнике, о Которых Вы не ЗналиСкачать

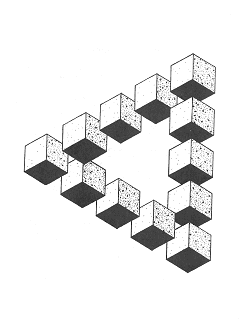
Треугольник из 12 кубов
Геометрические фигуры лучшие источник вдохновения для изобретения невозможных объектов. Например, возьмем простой куб. Каждый день мы видим их в огромном количестве в той или иной форме, как вы легко можете видеть из иллюстрации на соседней странице. Для построения этой фигуры мы взяли один из трибаров с предыдущей страницы и разбили его на кубы. При этом ничего не изменилось: новая фигура так же совершенно невозможна, как и предшествующая ей!
Эта фигура, состоящая из 12 кубов, была сконструирована на чертежной доске с помощью прямоугольного треугольника с углами в 30 и 60°. Чертежный треугольник использовали для того, чтобы вписать каждый куб в общую перспективу чертежа. Эффект невозможности, для создания которого использована эта перспектива, достигается неправильным расположением на переднем и заднем плане рядов кубов. По этому же принципу строится и трибар. Другими словами, рисунок основан на неправильном соединении правильных рядов кубов.
Видео:Бермудский треугольник | Почему? Вопросы мироздания | DiscoveryСкачать

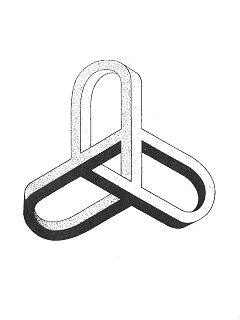
Крылатый трибар
«Крылатый трибар» еще одна разработка концепции трибара. Она показывает, как легко можно создать уникальные и интересные вариации на одну и ту же тему. Из трибара можно получить множество интересных фигур!
На протяжении долгого времени психологи использовали геометрические фигуры разного рода при изучении человеческой личности. С начала века было разработано более 200 фигур и иллюзий для анализа психологических аспектов зрительного процесса и умственной деятельности пациентов. Они рассматривали эти объекты и пытались понять их. При помощи таких экспериментов, когда глазу предлагалась противоречивая информация, было получено множество новых сведений о типах личности. Некоторые из этих фигур даже включают в себя невозможные объекты, похожие на этот.
Очень интересно наблюдать за человеком, рассматривающим невозможный объект, и так же интересно наблюдать за тем, как он пытается понять его. Невозможные объекты важны для психологов, выясняющих, что же привлекает внимание людей.
Видео:Как Выжить в 5 Критических СитуацияхСкачать

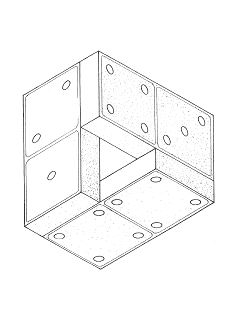
Тройное домино
Чтобы построить эту фигуру, состоящую из трех элементов, в реальности потребуется четыре элемента. Попытайтесь-ка сами смастерить ее, играя в домино! В обычном круге 360°. Здесь же замыкается 360-градусная петля, хотя в самом объекте всего лишь 270°! При ближайшем рассмотрении становится ясно, что данная фигура основана на неправильном повороте в перспективе. Здесь применен принцип, похожий на принцип построения невозможного трибара. В действительности эта фигура не что иное как трибар, в котором три основных элемента были заменены известными элементами из игры в домино.
Видео:Необъяснимые встречи | Проклятие Бермудского треугольника | DiscoveryСкачать

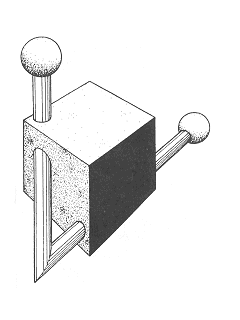
Кубик со штифтами
Эта более замысловатая версия трибара была придумана благодаря детским кубикам. Объект содержит два дополнительных компонента, похожих на штифты, которые пронизывают кубик и соединяются снаружи невероятным образом. Но только само по себе соединение делает невозможную фигуру возможной, по крайней мере на бумаге. То, что эта сложная фигура является треугольником, очевидно даже в этой простой композиции из двух элементов.
Видео:Места, Которые Загадочнее Бермудского ТреугольникаСкачать

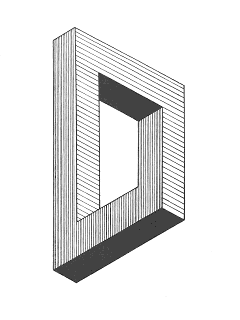
Усеченный трибар
Ознакомившись с трибаром и его бесчисленными вариациями, обратимся к еще одной, столь же любопытной фигуре. Усеченный трибар это трибар, один угол которого отрезали, «отсекли». В результате у фигуры получилось четыре стороны. Если бы этот объект был оконной рамой, то представьте себе, как сложно было бы вставить в него стекло! (Вот уж была бы головная боль!)
Так же, как и в случае с невозможным трибаром, поначалу глаз воспринимает эту фигуру как стереометрический объект, но потом как нечто похожее на оконную раму. Эта фигура не может существовать в реальности, но опять же на нее нельзя не обратить внимание Эффект «усеченного трибара» достигается как при помощи смещенной перспективы, так и благодаря неправильному соединению.
Видео:Бермудский Треугольник Реальность или Фантастика? Документальный фильм National Geographic 2021Скачать

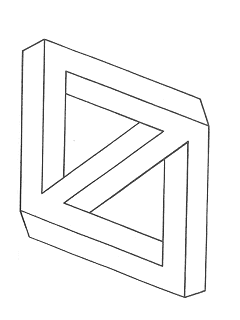
Перекрещенный ромб
Создателей этой загадочной фигуры, которая изображена на следующей странице, вдохновил вид скрещивающихся ферм, поддерживающих лестничную площадку в двухэтажном доме. Опять же принцип трибара здесь очевиден. Эта фигура представляет собой не что иное, как два трибара, соединенных вместе в форме ромба. Вы можете расширить эту конструкцию, присоединяя дополнительные трибары. Как уже говорилось ранее, Эшер в своей знаменитой композиции соединил вместе три трибара. Здесь нет никаких ограничений. Теоретически можно соединить много таких трибаров по образцу лоскутного одеяла или другого дизайна. Во всяком случае, мы предоставим читателю самому пририсовывать треугольники к этой коварной квадратной квазифигуре!
Видео:Что Мы Увидим Если Осушить ОкеанСкачать

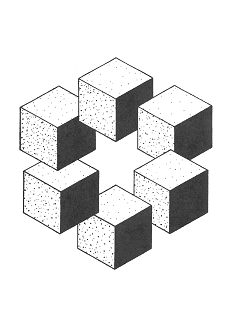
Головоломка из кубиков
Эта фигура еще одна версия известного трибара. На сей раз объект как бы поставлен соответствующим (хотя и невозможным) образом на дыбы на всеобщее обозрение. Из-за странной взаимосвязи между реальностью и фантазией кажется, что эта фигура слегка пикирует и парит в воздухе! Дополнительная иллюзия «полета» создается смещением акцентов на заднем и переднем плане.
Видео:100 Самых Необъяснимых и Загадочных Мест на ПланетеСкачать

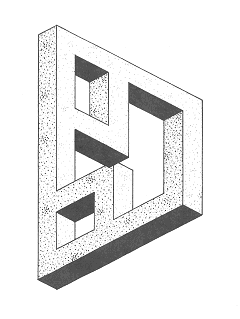
Усеченный деформированный трибар
«Усеченный деформированный трибар» является, в сущности, урезанным трибаром с небольшой внутренней вариацией. Он выглядит как сюрреалистический проект нового вида мебели, но эта фигура способна привести в замешательство любого плотника, который примет заказ на дюжину таких предметов. Это выразительное произведение мини-искусства может опять же дать толчок для развития массы новых идей по созданию всего, что угодно, начиная со стульев; для сада и заканчивая скульптурами для городской площади!
Визуальные виды искусства удовлетворяют огромное количество человеческих потребностей. Невозможные фигуры, похожие на эту, представляют собой увлекательное сочетание занимательности и развлечения. Их можно назвать «искусством для отдыха»
Видео:Гигантская Женщина Попала В Ловушку Крошечных Обитателей Бермудского ТреугольникаСкачать

Летучий шестиугольник
Эта новая интересная вариация трибара, основанная на симметрии и повторении, напоминает изображение, которое можно увидеть в калейдоскопе. Вы можете заметить, что основной лежащий в основе трибара принцип присутствует и в этой уникальной конструкции.
Как и многие трибары, данную фигуру относительно легко создать. Создается впечатление, как будто все, что нужно, это только гончарный круг, чтобы повернуть чертеж, и тогда все края фигуры станут одинаковыми. Можно легко увидеть, что, как и во всех фигурах типа трибара, в основании этой конструкции лежит треугольник.
Видео:10 Самых Странных Вещей Найденных На Дне ОкеанаСкачать

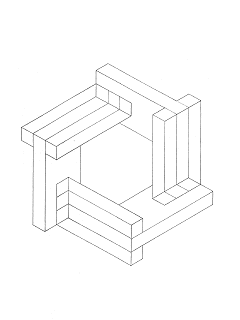
Прямоугольный триэдр (трехгранник)
В этом заключительном примере на тему трибаров можно увидеть еще один способ усовершенствования треугольника Пенроуза. Eсли вы думаете, что все возможности модели трибара исчерпаны, позвольте вас заверить, что новые идеи всегда будут появляться, это я вам обещаю!
В принципе, эта фигура имеет такие же правила построения, ка и остальные виды трибара. В основном это трехмерный равносторонний треугольник, составленный из прямоугольных тел. Пытаясь понять эту фигуру, вы неизбежно будете перескакивать взглядом с одного края на другой.
Видео:10 Мест на Земле, Которые Невозможны с Научной Точки ЗренияСкачать

Методические материалы проекта «Удивительные треугольники»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Презентация Александров проектt.ppt
Описание презентации по отдельным слайдам:
МКОУ «Высоковская СШ» Выполнил обучающийся 7 класса Александров Александр Руководитель: Яковская С.А. Проект
Цель: Систематизировать и расширить знания о треугольниках. Задачи проекта: изучить исторические сведения о треугольниках; найти информацию о том, где встречаются треугольники в окружающем нас мире. Гипотеза: без треугольников и в жизни, и в математике не обойтись.
Что такое треугольник? Треугольник — это геометрическая фигура, которая образована тремя отрезками, соединяющие три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла.
В глубокой древности вместе с астрономией появилась наука «тригонометрия». Слово «тригонометрия» произведено от греческих «треугольник» «меряю» Буквальное значение – «наука об измерении треугольников»
Треугольники в повседневной жизни
Треугольники в архитектуре
13-метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999 году в городе Перт (Австралия)
Треугольник Паскаля Самой известной математической работой Блеза Паскаля является трактат об «арифметическом треугольнике», образованном биномиальными коэффициентами (треугольник Паскаля), который имеет применение в теории вероятностей и обладает удивительными и занимательными свойствами.
Треугольник Рёло Треугольник Рёло – это область пересечения трех окружностей, построенных из вершин правильного треугольника. Они имеют радиус, равный стороне этого же треугольника. Он относится к разряду простых фигур (как круг), обладающих постоянной шириной. То есть если к нему провести две параллельные опорные прямые, то независимо от выбранного направления, расстояние между ними будет неизменным, в любой точке независимо от их длины.
Бермудский треугольник Бермудский треугольник – одно из самых мистических мест на нашей планете, изучить природу которого до сих пор не удалось человеку. Это загадочное место находится в Атлантическом океане, между тремя географическими точками: Пуэрто-Рико, Флоридой и Бермудскими островами. Эти точки образуют геометрические «вершины» Бермудского треугольника. Вот такая вот странная загадка этого места с условными границами простой геометрической фигуры. Загадка, которую вряд ли когда-нибудь удастся решить.
Поворотный треугольник — это соединение железнодорожных путей в виде треугольника,устраи- ваемое для разворота локомотива на 180°. Поворотные треугольники наиболее распространены на железных дорогах США,в России поворотных треугольников отно- осительно немного. Поворотный треугольник
Треугольники встречаться на дорогах – это дорожные знаки, которые называются Предупреждающие знаки ДОРОЖНЫЕ ЗНАКИ Дорожные знаки
Параллактический треугольник – сферический треугольник на небесной сфере, вершинами которого являются полюс (P), зенит (Z), и светило (X).Используется в астронавигации.С помощью него можно определить координаты места наблюдения, а также рассчитать моменты времени восхода и захода светил применительно к месту наблюдения, определить местное звёздное время. Параллактический треугольник
Треугольник Петрова — приём в русских шашках ,названный в честь знаменитого шашиста Александра Дмитриевича Петрова. При помощи такого приёма достигается ловля одинокой дамки тремя дамками. За рубежом носит название «способ Монтеро», «классический метод». Впервые опубликован в «Книге для играющих в шашки» Педро Руизо Монтеро в 1591 году. Треугольник Петрова
Треугольник — удушающий приём, одно из самых сильных удушений ногами. В данном приёме делается своеобразный замок ногами на шею противника. Этот приём был создан в начале XX века дзюдоистом Цутанэ Одой. Этот приём используется в дзюдо, бразильском джиу-джитсу, боевом самбо, а также в ММА Прием «Треугольник»
Треугольник — музыкальный инструмент, принадлежащий к группе ударных. Представляет собой металлический пруток, согнутый в треугольник с незам- кнутым концом. Этот инструмент считает- ся достаточно простым и чаще всего его применяют в симфоническом оркестре, где для исполнения некоторых сочинений известных композиторов он выступает в роли ведущего инструмента. Музыкальный инструмент
Вывод В процессе реализации проекта я узнал, что треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, поэтому эта фигура всегда имела широкое применение в практической жизни. В ходе работы я понял, что мы встречаем треугольники повсюду: в архитектуре, в музыке и даже в борьбе. Треугольник – распространённая фигура, также с ним связаны загадки и тайны природы. Таким образом, я подтвердил свою гипотезу, что без треугольников и в жизни, и в математике просто не обойтись.
Интернет – сайты: http://ru.wikipedia.org http://www-formula.ru http://with-art.livejournal.com http://www.ufolog.ru, http://www.yourfight.ru Литература Демпан И.Я. Мир чисел: «Рассказы о математике»- Издание 4-е 1982г Нагибин Ф.Ф.,Канин Е. С.Математическая шкатулка. Москва «Просвещение» 1984 г. Е . Е. Семёнов. Изучаем геометрию. Москва « Просвещение »1987г. Л.А.Бахтина. Час занимательной математики. Москва «Народное образование» 2003г. Ю.В.Прохоров , С.А .Теляковский. «Научное издательство –Большая Российская Энциклопедия». Москва 1996 г.
Выбранный для просмотра документ комментарии к слайдам.docx
Тема моего проекта «Удивительные треугольники».
В ходе его выполнения передо мной стояли задачи: узнать историю треугольника и найти информацию о том, где встречаются треугольники в окружающем нас мире.
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами, а отрезки – сторонами треугольника.
Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет. В Древней Греции изучение свойств треугольника достигает высокого уровня — это теорема Пифагора и формула Герона, которым более 2000 лет. Вся геометрия со времён «Начал» Евклида покоится на «трёх китах» — трёх признаках равенства треугольников.
За несколько тысячелетий геометры столь подробно изучили треугольник, что говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии. Тригонометрия («тригон»- по-гречески означает «треугольник»). С ней древние научились измерять воображаемые треугольники на небе, вершинами которых были звезды.
Знать жаждет любой школьник,
Что такое треугольник.
Треугольник — это клин,
Треугольником трамплин
Высится над миром,
Клином в небе журавли
Пролетают мимо.
Праздничная елка —
Тоже «треуголка».
Парус в море, всех ветров
На земле поборник,
С виду — треугольник.
И беляш, и пирамида —
Треугольнейшего вида.
Я коротко познакомлю вас с понравившимися мне треугольниками.
Треугольник Пенроуза — одна из основных невозможных фигур, известная также под названиями невозможный треугольник и трибар. Был открыт в 1934 году шведским художником Оскаром Реутерсвардом, который изобразил его в виде набора кубиков.
13-метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999 году в городе Перт (Австралия)
Самой известной математической работой Блеза Паскаля является трактат об «арифметическом треугольнике», образованном биномиальными коэффициентами (треугольник Паскаля), который имеет применение в теории вероятностей и обладает удивительными и занимательными свойствами.
Треугольник Рёло – это область пересечения трех окружностей, построенных из вершин правильного треугольника. Треугольник широко распространён и в архитектуре. Конструкция из двух дуг треугольника Рёло образует стрельчатую арку готического стиля.
Чтобы не ошибиться при строительстве пирамиды, древние египтяне прежде всего размечали на земле её основание в виде квадрата. Прямые углы квадрата они «чертили» с помощью верёвки. На ней завязывали узлы, делившие её на равные 12 равных частей. Верёвку натягивали в виде треугольника со сторонами, отношение между которыми равнялось 3:4:5. Угол, противоположенный самой длинной стороне, всегда оказывался прямым.
Бермудский треугольник – одно из самых мистических мест на нашей планете, изучить природу которого до сих пор не удалось человеку. Это загадочное место находится в Атлантическом океане, между тремя географическими точками: Пуэрто-Рико, Флоридой и Бермудскими островами. Эти точки образуют геометрические «вершины» Бермудского треугольника.
С 1945 года, это «дьявольское морское место» считается очень опасным для мореплавателей. Здесь происходило множество необъяснимых явлений. Дрейфующие суда с мертвыми экипажами, бесследные исчезновения самолетов и морских судов, выход из строя навигационных приборов, датчиков, радиопередатчиков, часов – вот, чем прославился на весь мир этот морской треугольник.
Треугольники встречаются в строительстве железнодорожных мостов. Треугольники делают надёжными конструкции высоковольтными линии электропередач. Три металлические или деревянные планки, закреплённые в их концах так, чтобы получился контур треугольника. Его изменить нельзя. Это объясняется свойством жёсткости: если заданы стороны треугольника, то форма его уже не изменится. Это свойство широко применяется на практике. В частности в строительстве.
Поворотный треугольник — это соединение железнодорожных путей в виде треугольника, устраиваемое для разворота локомотива на 180°. Поворотные треугольники наиболее распространены на железных дорогах США.
Треугольники встречаться на дорогах – это дорожные знаки,
которые называются предупреждающими знаками.
Параллактический треугольник – сферический треугольник на небесной сфере, вершинами которого являются полюс , зенит и светило.
Треугольник Петрова — приём в русских шашках, названный в честь знаменитого шашиста Александра Дмитриевича Петрова. При помощи такого приёма достигается ловля одинокой дамки тремя дамками.
Треугольник — удушающий приём, одно из самых сильных удушений ногами. В данном приёме делается своеобразный замок ногами на шею противника. Этот приём используется в дзюдо, бразильском джиу-джитсу, боевом самбо.
Треугольник — музыкальный инструмент, принадлежащий к группе ударных. Представляет собой металлический пруток, согнутый в треугольник с незамкнутым концом. Его применяют в симфоническом оркестре.
В процессе реализации проекта я узнал, что треугольник – самая простая замкнутая прямолинейная фигура. Одна из первых фигур, свойства которых человек узнал еще в глубокой древности, поэтому эта фигура всегда имела широкое применение в практической жизни. В ходе работы я понял, что мы встречаем треугольники повсюду: в архитектуре, в музыке и даже в борьбе. Треугольник – распространённая фигура, также с ним связаны загадки и тайны природы. Таким образом, я подтвердил свою гипотезу, что без треугольников и в жизни, и в математике просто не обойтись.
Выбранный для просмотра документ реферат.docx
МКОУ «Высоковская СШ»
Выполнил обучающийся 7 класса
Руководитель: Яковская С.А.
систематизировать и расширить знания о треугольниках.
изучить исторические сведения о треугольниках;
найти информацию о том, где встречаются треугольники в окружающем нас мире.
Где в жизни нам приходится сталкиваться с треугольником?
Можно ли представить жизнь без треугольника?
Зачем нам нужен треугольник?
без треугольников и в жизни, и в математике не обойтись.
Введение
Треугольник (в евклидовом пространстве) — это геометрическая фигура, которая образована тремя отрезками, соединяющие три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Треугольник — это многоугольник, у которого имеется три угла.
Мы знакомы с разными многоугольниками: треугольник, четырехугольник, пятиугольник и т.д. Почему же именно треугольник считают символом геометрии? Потому что треугольник – это многоугольник с наименьшим количеством сторон. Действительно, построить многоугольник с двумя сторонами не получится. Ведь для того чтобы получился многоугольник нужна третья сторона.
Самым простым многоугольником является треугольник. Но простым – не значит не интересным. Треугольник — неотъемлемая часть окружающего нас мира, так как используется в быту и различных устройствах.
С древнейших времен и до наших дней математики занимаются изучением треугольника.
Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. С этого и началась геометрия – «землемерие» (от греческого «гео» – «земля» и «метрео» «измеряю»). Древние землемеры выполняли геометрические построения, измеряли длины и площади. Астрологи рассчитывали расположение небесных светил – все это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике. Изображение треугольников и задачи на треугольники встречаются в египетских папирусах, которым более 4000 лет, в старинных индийских книгах и других древних документах. Уже тогда была известна теорема, получившая впоследствии название теоремы Пифагора, которая применялась для построения прямых углов на местности с помощью веревочного треугольника со сторонами 3, 4, 5 (египетский треугольник). Древнегреческий ученый Герон впервые применил знак «∆» вместо слова «треугольник».
Учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, затем в школе Пифагора. Древние греки решили упорядочить накопленные сведения о треугольнике и написали много трудов. Наиболее совершенной оказалась работа Евклида «Начала»(365-300 до н.э.). «Начала» Евклида состоят из тринадцати книг (отделов, или частей). В 1-ой книге рассматриваются основные свойства треугольников, прямоугольников, параллелограммов и производится сравнение их площадей. Заканчивается книга теоремой Пифагора.
Архимед (287-212 гг. до н. э.) родился в городе Сиракузы на острове Сицилия. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики.
Важнейшей заслугой Фалеса в области математики: перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии. Фалес Милетский жил в самом конце 7 — первой половине 6 в. до н. э. Фалес был уроженцем греческого торгового города Милета, расположенного в Малой Азии на берегу Эгейского Моря.
Рене Декарт заложил основы аналитической геометрии. Геометрия Декарта оказала огромное влияние на развитие математики, и почти 150 лет алгебра и аналитическая геометрия развивались преимущественно в направлениях, указанных Декартом.
Понселе Жан Виктор (1788-1867) , французский математик и инженер, заложил основы проективной геометрии. В 1822 году французский математик и механик Жан Виктор Понселе опубликовал «Трактат о проективных свойствах фигур».
Леонард Эйлер — один из величайших математиков XVIII столетия, родился в 1707 г. Им были открыты новые теоремы о свойствах треугольника.
Как известно, с давних времен, существует целая наука тригонометрия («тригон»- по-гречески означает «треугольник»). С ее помощью можно было, измерив одну сторону и два угла треугольника, найти длины всех его сторон. Но еще ранее с ее помощью научились измерять воображаемые треугольники на небе, вершинами которых были звезды. Тригонометрия, как отдельный предмет, впервые рассматривается в труде азербайджанского математика и астронома Насиреддина Туей (1201-1274) «Трактат о полном четырехстороннике». В Европе аналогичное открытие сделал немецкий ученый Иоганн Мюллер (1436-1476) в сочинении «О треугольниках всех видов».
Красивая теорема Наполеона. «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника».
Открытие в геометрии треугольника есть и в прошлом веке. В 1904 году американский математик Эдвард Морли вывел теорему о трисектрисах угла, теоремы о замечательных точках треугольника.
Треугольники вокруг нас
Треугольники в архитектуре
Треугольник Пенроуза — одна из основных невозможных фигур, известная также под названиями невозможный треугольник и трибар.
Был открыт в 1934 году шведским художником Оскаром Реутерсвардом, который изобразил его в виде набора кубиков. В 1980 году этот вариант невозможного треугольника был напечатан на шведских почтовых марках.
13-метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999 году в городе Перт (Австралия).
Треугольник Паскаля
Самой известной математической работой Блеза Паскаля является трактат об «арифметическом треугольнике», образованном биномиальными коэффициентами (треугольник Паскаля), который имеет применение в теории вероятностей и обладает удивительными и занимательными свойствами. Мартин Гарднер пишет в книге «Математические новеллы» (М., Мир, 1974): «Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике».
Треугольник Рёло – это область пересечения трех окружностей, построенных из вершин правильного треугольника. Они имеют радиус, равный стороне этого же треугольника. Он относится к разряду простых фигур (как круг), обладающих постоянной шириной. То есть если к нему провести две параллельные опорные прямые, то независимо от выбранного направления, расстояние между ними будет неизменным, в любой точке независимо от их длины.
Франц Рёло впервые показал возможность связи между основами механики и конструирования. То есть связал теорию и практические проблемы конструирования. Что позволило создавать механизмы в совокупности их функциональных возможностей с внешней привлекательностью/эстетичностью. Отсюда Рёло стали считать поэтом механики. Что позволило последователям в корне пересмотреть имеющиеся в ней теории. Треугольник широко распространён и в архитектуре. Конструкция из двух дуг треугольника Рёло образует стрельчатую арку готического стиля. А окна в форме Рёло стоят в Брюгге в церкви Богоматери. Как орнамент он присутствует и на оконных решетках швейцарской коммуны Отрив и цистерцианского аббатства.
Чтобы не ошибиться при строительстве пирамиды, древние египтяне прежде всего размечали на земле её основание в виде квадрата. Прямые углы квадрата они «чертили» с помощью верёвки. Но верёвка была не простая. На ней завязывали узлы, делившие её на равные 12 равных частей. Верёвку натягивали в виде треугольника со сторонами, отношение между которыми равнялось 3:4:5. Угол, противоположенный самой длинной стороне, всегда оказывался прямым. Почему? Это объясняет теорема Пифагора, самая популярная, быть может, из всех теорем.
Бермудский треугольник – одно из самых мистических мест на нашей планете, изучить природу которого до сих пор не удалось человеку. Это загадочное место находится в Атлантическом океане, между тремя географическими точками: Пуэрто-Рико, Флоридой и Бермудскими островами. Эти точки образуют геометрические «вершины» Бермудского треугольника.
Уже много лет, а точнее — с 1945 года, это «дьявольское морское место» считается очень опасным для мореплавателей. Здесь происходило множество необъяснимых явлений. Дрейфующие суда с мертвыми экипажами, бесследные исчезновения самолетов и морских судов, выход из строя навигационных приборов, датчиков, радиопередатчиков, часов – вот неполный список того, чем прославился на весь мир этот морской треугольник.
Многие ученые, астрономы, физики, математики, географы, и даже военные службы пытались разгадать мистику загадочных явлений, однако эти исследования не стали успешными. На сегодняшний день человеческий мир владеет только обыкновенными догадками, которые не дают однозначного ответа – что это за странное географическое место, что видят люди, попадая туда, куда пропадают исчезнувшие корабли и самолеты. Вот такая вот странная загадка этого места с условными границами простой геометрической фигуры. Загадка, которую вряд ли когда-нибудь удастся решить.
Треугольники в строительстве
Треугольники встречаются в строительстве железнодорожных мостов. Треугольники делают надёжными конструкции высоковольтными линии электропередач. Три металлические или деревянные планки, закреплённые в их концах так, чтобы получился контур треугольника изменить нельзя. Это объясняется свойством жёсткости, если заданы стороны треугольника, то форма его уже не изменится. Это свойство широко применяется на практике. В частности в строительстве.
Поворотный треугольник — это соединение железнодорожных путей в виде треугольника, устраиваемое для разворота локомотива на 180°. Поворотные треугольники наиболее распространены на железных дорогах США, в России поворотных треугольников относительно немного.
Дорожные знаки
Треугольники встречаться на дорогах – это дорожные знаки,
которые называются предупреждающие знаки.
Параллактический треугольник – сферический треугольник на небесной сфере, вершинами которого являются полюс (P), зенит (Z), и светило (X). Используется в астронавигации. С помощью него можно определить координаты места наблюдения, а также рассчитать моменты времени восхода и захода светил применительно к месту наблюдения, определить местное звёздное время.
Треугольник Петрова — приём в русских шашках, названный в честь знаменитого шашиста Александра Дмитриевича Петрова. При помощи такого приёма достигается ловля одинокой дамки тремя дамками. За рубежом носит название «способ Монтеро», «классический метод». Впервые опубликован в «Книге для играющих в шашки» Педро Руизо Монтеро в 1591 году.
Треугольник — удушающий приём, одно из самых сильных удушений ногами. В данном приёме делается своеобразный замок ногами на шею противника. Этот приём был создан в начале XX века дзюдоистом Цутанэ Одой. Этот приём используется в дзюдо, бразильском джиу-джитсу, боевом самбо.
Треугольник — музыкальный инструмент, принадлежащий к группе ударных. Представляет собой металлический пруток, согнутый в треугольник с незамкнутым концом. Этот инструмент считается достаточно простым и чаще всего его применяют в симфоническом оркестре, где для исполнения некоторых сочинений известных композиторов он выступает в роли ведущего инструмента.
В процессе реализации проекта я узнал, что треугольник – самая простая замкнутая прямолинейная фигура. Одна из первых фигур, свойства которых человек узнал еще в глубокой древности, поэтому эта фигура всегда имела широкое применение в практической жизни. В ходе работы я понял, что мы встречаем треугольники повсюду: в архитектуре, в музыке и даже в борьбе. Треугольник – распространённая фигура, также с ним связаны загадки и тайны природы. Таким образом, я подтвердил свою гипотезу, что без треугольников и в жизни, и в математике просто не обойтись.
Видео:Ученые установили камеру в гроб. Увиденное в процессе на наблюдения всех шокировало.Скачать

Треугольники в жизни человека
Работа моего ученика Андреасян Меружана. Подготовлена для школьной научно-практичкой конференции.
Видео:В Бермудском треугольнике могут скрываться гигантские кальмары!Скачать

Скачать:
| Вложение | Размер |
|---|---|
| treugolnik_v_zhizni_cheloveka.ppt | 1.87 МБ |
| treugolnik_v_zhizni_cheloveka.doc | 68 КБ |
Предварительный просмотр:
Видео:Пропавший Самолёт Приземлился 37 Лет Спустя. Что Произошло?Скачать

Подписи к слайдам:
«Треугольник в жизни человека» Выполнил работу: Ученик 7 «Б» МОУ «Средняя школа № 46» Андреасян Меружан
Содержание: Введение Глава I — Основная часть 1.1 Интересные открытия, связанные с числами 1.2Исторические факты, подтверждающие гипотезу 1.3 Мои собственные исследования Глава II . 2.1 Заключение 2.2 Список литературы, ссылки. 2.3 Приложение
Объект исследования : «Треугольник» Предмет исследования : «Значение треугольника в жизни человека» Цель : Найти и исследовать значение треугольника в жизни человека, чтобы понять жизненную необходимость треугольника в быту.
Задачи : 1. Найти учёного или человека открывшего 2. Найти интересные факты про треугольник 3. Найти объекты или предметы, где используется треугольник. Гипотеза : Если треугольник используют в быту и в повседневной жизни, то значит он жизненно необходим. Методы исследования : 1. Метод обобщения 2. Метод выявления 3. Метод опроса 4. Метод анализа
Кто же открыл треугольник. Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник. Так как Геометрия это очень старая наука и была известна ещё в Древнем Египте, учёного открытого треугольник неизвестно. По выявленным данным в интернете и книгам понятно, что, скорее всего треугольник открыл жрец. Так как жрецы были самими умными людьми в те время.
Шейные треугольники Каждая половина шеи по бокам от срединной линии, проведенной от подбородка до яремной вырезки, делится грудино-ключично-сосцевидной мышцей на два треугольника – передний и задний. Каждый из указанных треугольников посредством мышц шеи делится на ряд меньших треугольников.
Шейные треугольники Поднижнечелюстной треугольник 2. Сонный треугольник 3. Лопаточно — трахеальный треугольник 4. Лопаточно — ключичный треугольник 5. Лопаточно — трапециевидный треугольник 6. Позадичелюстная ямка 7. Подбородочный треугольник
Треугольник в чакрах людей
Треугольник в гадании Схема и значение карт Таро в раскладе на ситуацию “Треугольники” Карта 1 – Ваша сильная сторона или преимущество в ситуации в данный момент Карта 3 – Ваша слабая сторона в ситуации, в чём вы уязвимы в данный момент Карта 2 – Перспективы и возможность исполнения ваших надежд и планов Карта 4 – Что сейчас важно для развития ситуации Карта 5 – С чем могут быть связаны основные препятствия и трудности Карта 6 – Что говорит против изменений или вашего участия в событиях Карта 7 – Что работает на вас, что вы можете использовать, на что опереться Карта 8 – Из какого источника или какую помощь вы можете получить Карта 9 – Результат развития ситуации, итог событий в будущем Карта 10 – Что важно для достижения результата, на что обратить внимание Карта 11 – Что не важно в ситуации, на что не тратить силы и время
Треугольник на 1 долларовой купюре
Здания из Треугольника
Треугольник в природе
Треугольники в жизни человека Свойство жесткости треугольника широко используют в практике. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку. Такой же принцип используются при установке кронштейна, при строительстве железных конструкций. Высоковольтные линии электропередачи. Треугольники делают конструкции надежными, а так же они используются в конструкции мостов. В опросе приняли участие 20 человек (ребят). Некоторые люди написали даже несколько объектов. И вот результаты опроса:
Опрос Учащиеся (класс) Объекты (предметы) написанными детьми Сколько человек Учащиеся 3 класса СЫР 1 Учащиеся 3 класса ПИРАМИДА 2 Учащиеся 3 класса КРЫША 2 Учащиеся 3 класса ЛИНЕЙКА (УГОЛЬНИК) 2 Учащиеся 3 класса МАГНИТ 2 Учащиеся 3 класса БЕРМУДСКИЙ 1 Учащиеся 3 класса НИЧЕГО НЕ НАПИСАЛИ 12
Продолжение следует… И это ещё не всё!
Видео:Что стало с "Циклопом"? | Проклятие Бермудского треугольника | DiscoveryСкачать

Предварительный просмотр:
«МОУ «Средняя школа №46»»
Научно – исследовательская конференция секции математика
Ученик 7 «Б» класса
МОУ «Средняя школа № 46»
Учитель Алгебры и
Бойцева Ирина Юрьевна
1.1 Интересные открытия, связанные с треугольниками………………………………………стр.
- Исторические факты, подтверждающие гипотезу…………………………………стр.
1.3 Мои собственные исследования…………………………………………………. стр.
2.2 Список литературы, ссылки…………………………………………………………. стр.
Тема нашего исследования – «Треугольник в жизни человека».
-Что такое треугольник?
– Треугольник — это геометрическая фигура, состоящая из трёх точек и трёх отрезков, которые их соединяют.
Он постоянно фигурирует в нашей жизни, начиная нашей одеждой и продолжая улицами, переулками, домами и т.д. Задумывались ли вы хотя бы один раз когда-либо о значении треугольника в жизни человека. Что скрывается в обычных незамысловатых предметах? И почему треугольник всё чаще начали использовать в повседневной жизни? На самом деле, не зря существует целая наука Геометрия, которая занимается изучением геометрических фигур. Попытаемся разобраться в основах теории треугольника. Могут ли они подсказать нам верный путь развития?
Объект исследования : «Треугольник»
Предмет исследования : «Значение треугольника в жизни человека»
Цель : Найти и исследовать значение треугольника в жизни человека, чтобы понять жизненную необходимость треугольника в быту.
1. Найти учёного или человека открывшего треугольник
2. Найти интересные факты про треугольник
3. Найти объекты или предметы, где используется треугольник
Гипотеза : Если треугольник используют в быту и в повседневной жизни, то значит, он жизненно необходим.
1. Метод обобщения
2. Метод выявления
4. Метод анализа
Кто же открыл треугольник.
Название науки «Геометрия» древнегреческого происхождения, и обозначает «землемерие».
Первые геометрические факты найдены в Вавилонских клинописных таблицах и Египетских папирусах (III тысячелетие до нашей эры), а также в других источниках. Люди изучали её, приобретая опыт из жизни, а поэтому в то время наука эта не являлась точной.
И только в VI веке до нашей эры древнегреческий учёный Фалес начал получать геометрические сведения с помощью доказательств.
Так как Геометрия это очень старая наука и была известна ещё в Древнем Египте, учёный, который открыл треугольник, неизвестен. По выявленным данным в интернете и книгам понятно, что, скорее всего треугольник открыл жрец. Жрецы – духовные просветители, которые верили что они посланники Бога. Жрецы были самими умными людьми в те времена и, науку изучая, они держали её в строжайшей тайне.
В III до нашей эры греческий учёный Евклид написал сочинение «Начала» и почти два тысячелетия Геометрия изучалась по этой книге. В том числе и треугольник.
Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник.
Понятие “равенство фигур” было известно в геометрии еще со времен Евклида и использовалось при решении задач. Используя равные треугольники, математик Фалес первым решил задачу о вычислении расстояния от берега до корабля. Как вы думаете, как можно узнать это расстояние? (надо куда вставить запехать)
Математик Фалес использовал для решения этой задачи равные треугольники: построив на земле треугольник, равный треугольнику “на воде”, и измерив расстояние на суше, он точно указал расстояние от берега до корабля.
Интересные факты про треугольник.
Недавно на дне бермудского треугольника было обнаружено пирамида. Учёные на протяжении многих лет не могут найти устойчивое доказательство того почему в Бермудском треугольники исчезают из вида радаров корабли и самолёты. До сих пор это самое загадочное чудо Земли. Оказалось, что эти пирамиды не похоже на те, которые расположены в Египте. Они созданы из неизвестного материала, по всем параметрам похожего на гладкую керамику или отшлифованное стекло. Также по размерам им уступает знаменитая пирамида Хеопса 2,5-3 раза. Хотя предварительные данные говорят о том, что их возраст не более половины тысячелетия. Историки утверждают, что пирамиды являются остатками комплекса древней цивилизации Атлантов, которые жили на легендарном древнем острове Атлантида. Первые источники упоминания этого острова были у древнегреческого философа Платона – ученика Сократа – в его диалогах «Тимей» и «Критий». Легенда гласит, что 9 тыс. лет назад Атлантида ушла на океанское дно за один день из-за произошедшей тогда масштабной катастрофы. На сегодняшний день ученые считают эту легенду мифом.
Треугольник так же используется в гадании. В картах Таро используется расклад карт «Треугольник».
Схема и значение карт Таро в раскладе на ситуацию “Треугольники”
Карта 1 – Ваша сильная сторона или преимущество в ситуации в данный момент
Карта 3 – Ваша слабая сторона в ситуации, в чём вы уязвимы в данный момент
Карта 2 – Перспективы и возможность исполнения ваших надежд и планов
Карта 4 – Что сейчас важно для развития ситуации
Карта 5 – С чем могут быть связаны основные препятствия и трудности
Карта 6 – Что говорит против изменений или вашего участия в событиях
Карта 7 – Что работает на вас, что вы можете использовать, на что опереться
Карта 8 – Из какого источника или какую помощь вы можете получить
Карта 9 – Результат развития ситуации, итог событий в будущем
Карта 10 – Что важно для достижения результата, на что обратить внимание
Карта 11 – Что не важно в ситуации, на что не тратить силы и время.
📽️ Видео
Это Существо в Египте Засняли на КамеруСкачать

Бермудский Треугольник - Загадка раскрыта!Скачать

СЕКРЕТЫ ПЛАНЕТЫ ЗЕМЛЯ. Большой документальный фильмСкачать


















