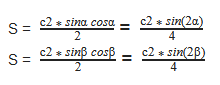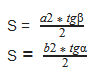О чем эта статья:
площадь, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Основные определения
- Формула для нахождения площади прямоугольного треугольника через катеты
- Формула для нахождения площади прямоугольного треугольника через гипотенузу
- Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
- Формулы нахождения площади прямоугольного треугольника через катет и угол
- Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
- Задача 2 «Определение максимальной площади треугольника»
- Треугольник с наибольшею площадью
- 📸 Видео
Видео:Найдите площадь прямоугольного треугольника, если сумма его катетов равна 15, а гипотенуза равна 13Скачать

Основные определения
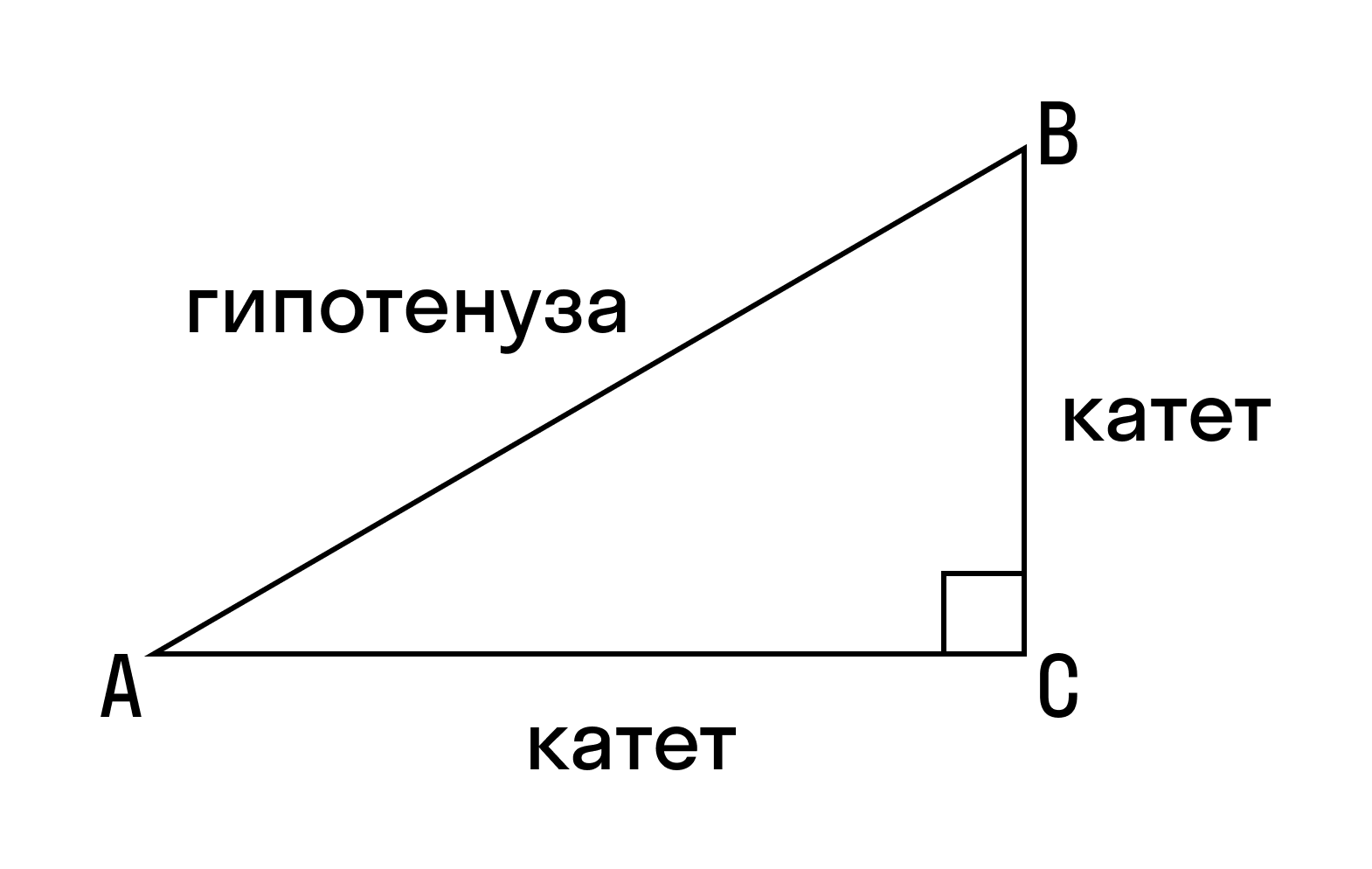
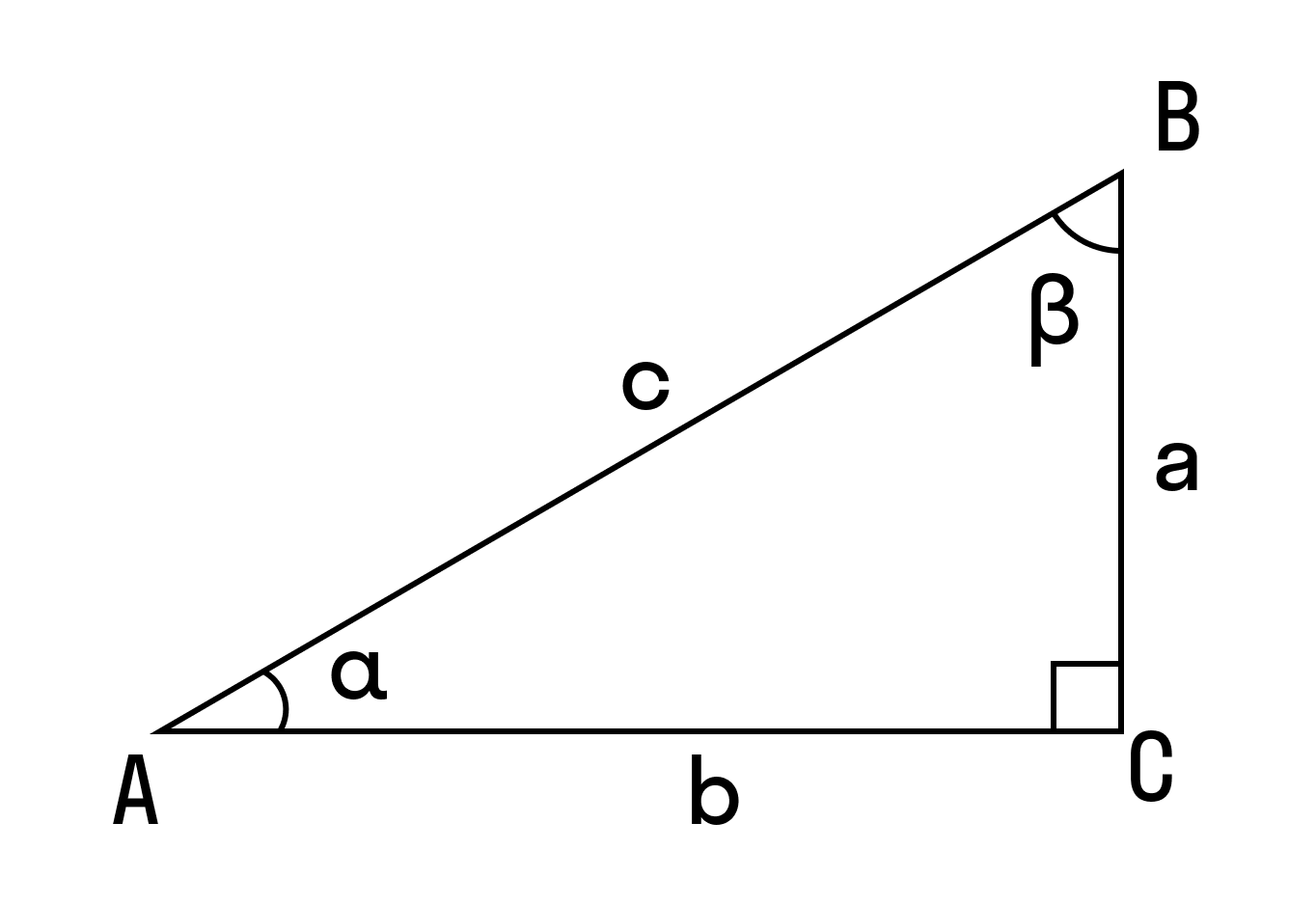
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
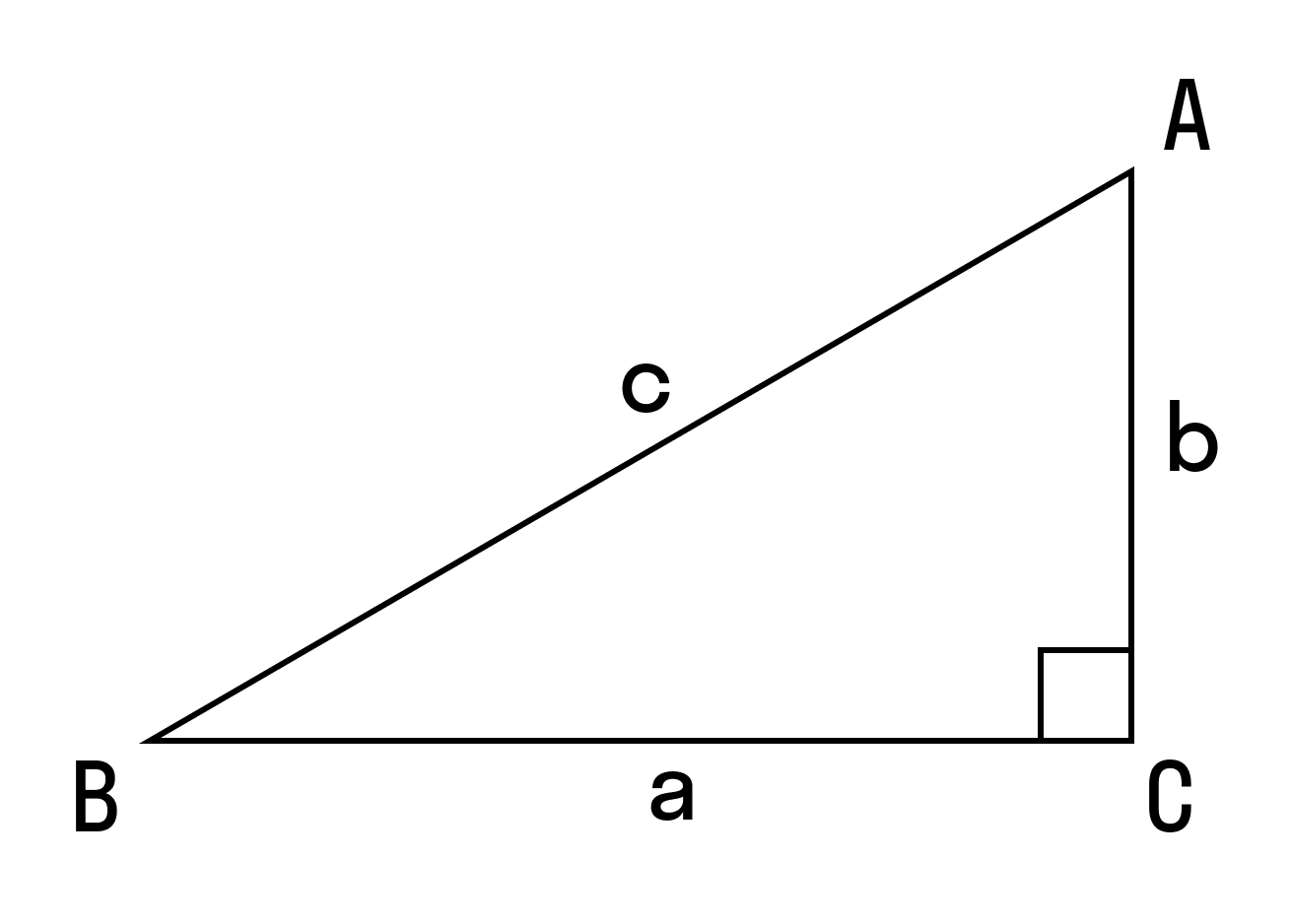
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Видео:4 класс, 25 урок, Площадь прямоугольного треугольникаСкачать

Формула для нахождения площади прямоугольного треугольника через гипотенузу
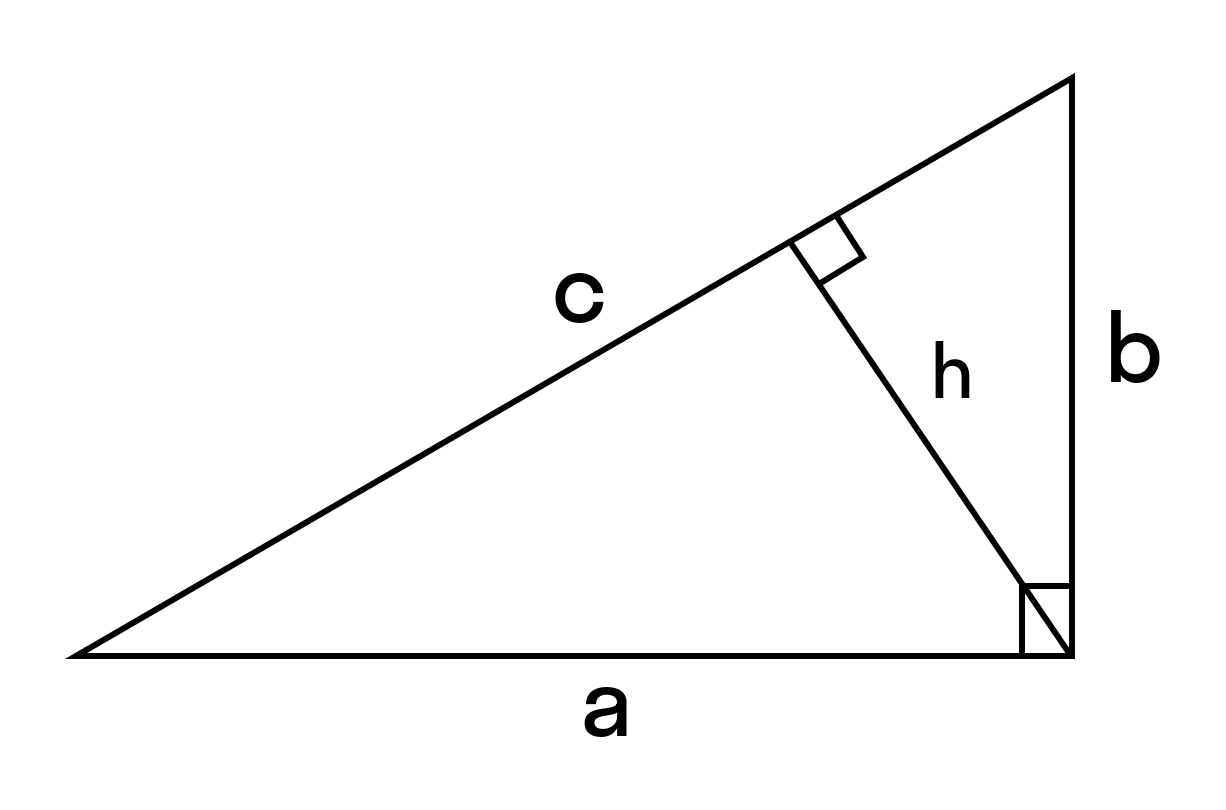
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
где с — гипотенуза,
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
Видео:КАК НАЙТИ ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
α, β — острые углы
Видео:Математика 4 Площадь прямоугольного треугольникаСкачать

Формулы нахождения площади прямоугольного треугольника через катет и угол
α, β — острые углы
Видео:Площадь прямоугольного треугольникаСкачать

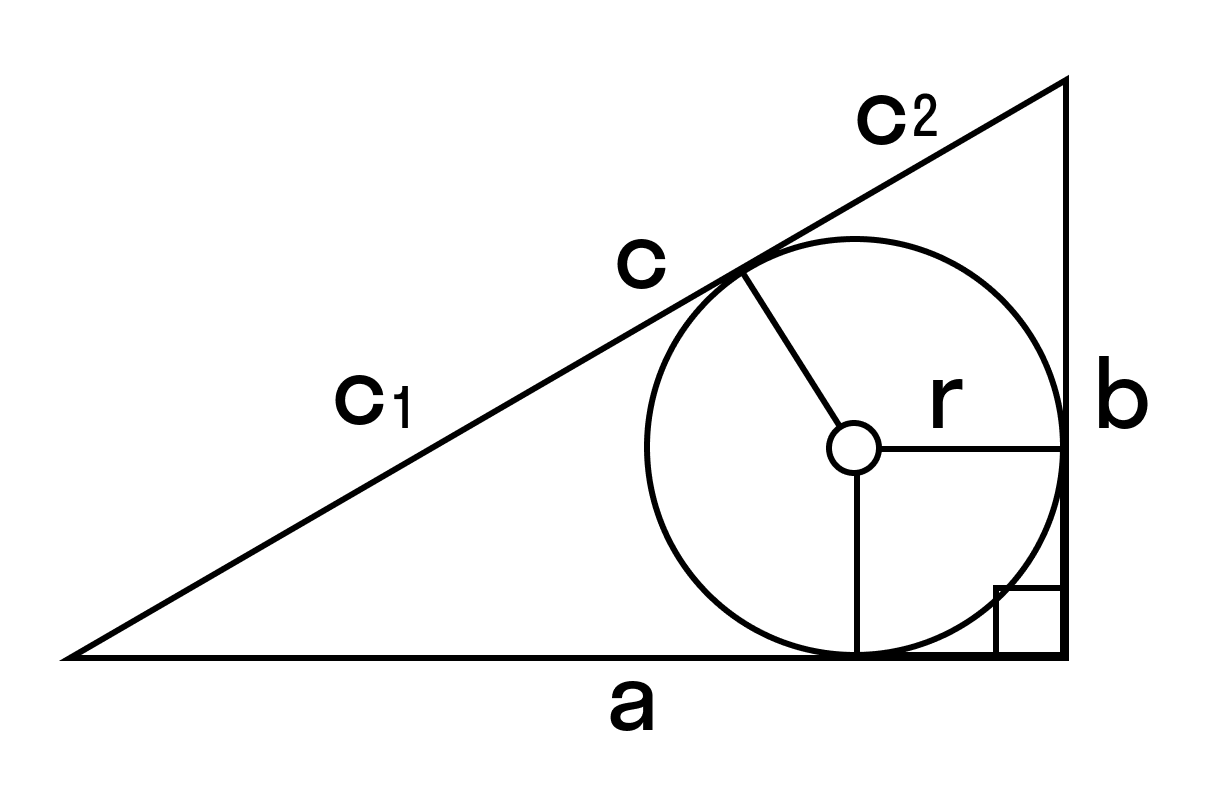
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Задача 2 «Определение максимальной площади треугольника»
| Дата | 13.04.2019 |
| өлшемі | 109 Kb. |
| #96226 | |
| түрі | Задача |
- Бұл бет үшін навигация:
- Исходные данные: Гипотенуза c Катет а Расчетные данные
- Составим геометрическую модель: с Этап 2. Разработка компьютерной модели.
- Вывод
- Этап 3. Анализ результатов моделирования. Вывод.
| Эксперимент 3: | Шаг изменения первого катета 1см | |
| Длина гипотенузы | один из катетов | площадь |
| 5 | 3 | 6 |
| 10 | 7 | 24,9 |
| 12 | 8 | 35,7 |
Вывод: При увеличении длины гипотенузы, мы наблюдаем увеличении катета, и максимальной площади.
Эксперимент 4.
Определим максимальное значение при длине шага Δb=0,3.
Изменим значение в ячейке «B5» с 1 на 0,3 и проверим результаты для 5, 10 и 12 см.
Сравним полученные результаты
| Эксперимент 3: | Шаг изменения первого катета 1см | |
| Длина гипотенузы | один из катетов | площадь |
| 5 | 3 | 6 |
| 10 | 7 | 24,9 |
| 12 | 8 | 35,7 |
| Эксперимент 4: | Шаг изменения первого катета 0,3см | |
| Длина гипотенузы | один из катетов | площадь |
| 5 | 3,6 | 6,25 |
| 10 | 7,2 | 24,98 |
| 12 | 8,4 | 35,99 |
Вывод: При уменьшении длины шага, мы получаем более точные значения максимальной площади.
Эксперимент 5.
Теперь нам нужно подобрать длину гипотенузы для заданных площадей: 54 см 2 , 96 см 2 и
150 см 2 . После проведения подбора мы получим следующие значения:
| Эксперимент 5: | Подбор длины гипотенузы Длина гипотенузы | один из катетов | площадь | |
| 15 | 9 | 54 | ||
| 20 | 12 | 96 | ||
| 25 | 15 | 150 | ||
Вывод: С помощью данной модели, можно не только определить максимальную площадь, если мы знаем длину катета и гипотенузы, но и вычислить длину катета по заданному значению площади.
Этап 3. Анализ результатов моделирования.
Вывод. В результате проведения эксперимента, мы научились составлять математическую и геометрическую модель, для расчета площади прямоугольного треугольника с помощью табличного процессора. Также мы научились анализировать результаты и проводить расчеты с большей точностью.
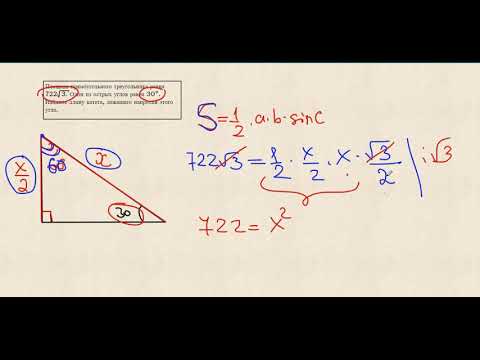
Видео:Площадь прямоугольного треугольника равна 200√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Треугольник с наибольшею площадью
Какую форму нужно придать треугольнику, чтобы при данной сумме его сторон он имел наибольшую площадь?
Мы уже заметили раньше (см. «Участки другой формы»), что этим свойством обладает треугольник равносторонний. Но как это доказать?
Площадь S треугольника со сторонами а, Ь, с и периметром а + b + с = 2р выражается, как известно из курса геометрии,так:
откуда
Площадь S треугольника будет наибольшей тогда же, когда станет наибольшей величиной и ее квадрат S 2 , S 2
или выражение —, где р, полупериметр, есть, согласно Р
условию, величина неизменная. Но так как обе части равенства получают наибольшее значение одновременно, то вопрос сводится к тому, при каком условии произведение
становится наибольшим. Заметив, что сумма этих трех множителей есть величина постоянная,
мы заключаем, что произведение их достигнет наибольшей величины тогда, когда множители станут равны, т.е. когда осуществится равенство
откуда
Итак, треугольник имеет при данном периметре наибольшую площадь тогда, когда стороны его равны между собою.
📸 Видео
Известна площадь прямоугольного треугольника и один из острых углов. Найти противолежащий катетСкачать
№472. Площадь прямоугольного треугольника равна 168 см2. Найдите его катеты, если отношениеСкачать

№471. Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11см;Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Площадь прямоугольного треугольникаСкачать

Урок 38. Площадь треугольника, прямоугольного треугольника, ромбаСкачать

Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Площадь прямоугольного треугольника равна (242√3)/3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Площадь прямоугольного треугольника равна 364,5∙√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Площадь прямоугольного треугольникаСкачать

Задача, которую исключили из экзамена в АмерикеСкачать