Движение колеса в окружности (6 видео) | Курс школьной геометрии

Геометрия движения колес или почему они поворачивают под разным углом

Вы иногда обращали внимание под каким углом поворачивают передние и задние колеса? Автомобилисты, которые хоть раз этим вопросом интересовались, заметили, что они поворачивают под разным углом. С первого взгляда можно подумать, что это неправильно и пора посетить станцию технического обслуживания. Не спешите – это всего лишь техническое решение, которое также представлено в спорткарах. Пришло время раскрыть перед Вами этот мировой заговор и тайну глобального масштаба.

Содержание

Почему колеса поворачиваются под разными углами?
Особенности просчета геометрии колес
Парадокс колеса
Новое в блогах
Парадокс Аристотеля о движении двух колес
📹 Видео

Видео:Вращательное движение. 10 класс.Скачать

Почему колеса поворачиваются под разными углами?

Ответ на самом деле очевиден. Достаточно представить только ситуацию, когда транспортное средство передвигается по направлению часовой стрелки по кругу. В такой ситуации окружность движения правого колеса намного меньше, чем получается левая окружность. Потому если машина едет с одной и той же скоростью, колеса транспортного средства на идентичной оси вращаются с различным скоростным режимом.

Теперь вернемся к тому, что они поворачиваются под одинаковым углом. Это будет провоцировать стремление внутреннего колеса двигаться по аналогии с наружным, но оно будет проскальзывать. Идентично будет вести себя и наружное. Такое движение транспортного средства во время маневров будет непредсказуемым, провоцирующим глобальный износ резины. Для наглядного примера советую обратить внимание на многоосные тележки прицепов и грузовых машин: шина изнашивается неравномерно и очень быстро.

Видео:Движение колеса без проскальзывания, качение | Олимпиадная физика, кинематика | 9 – 11 классСкачать

Особенности просчета геометрии колес

Описанная выше проблема появилась задолго до того времени, как в широком обиходе появились автомобили. К сожалению, идентичная ситуации встречалась также у повозок, в которые запрягались лошади. Именно для таких повозок и было разработано первое рулевое управление, решающее такую неприятность.

В далеком 1817 году Георг Ланкеншпергер изобрел решение проблемы, а спустя 12 месяцев в Великобритании оно было запатентовано Рудольфом Аккерманом, помощником изобретателя. С того периода этот принцип носит названия Аккермана. Для обеспечения правильных поворотов колесной базы, геометрия рулевой трапеции рассчитывается по одной единственной схеме.

Согласно с особенностями такого принципа, поперечная рулевая тяга всегда меньше по длине, чем ось управления, и смещается за ней. При этом между центром задней оси транспортного средства и осью поворота передних колес находятся рулевые рычаги, которые отвечают за поворот. Именно потому во время поворота колеса будут демонстрировать разные углы: наружное под меньшим, а внутреннее – под большим углом. Эти параметры не влияют на центр окружности, он остается без изменений. Предлагаю Вам обратить внимание на схематическое изображение процесса. Возможно, таким образом принцип будет более понятным.

Принцип геометрии движения идентичен для всех автомобилей, которые используются в частном и промышленном порядке. Но для гоночных транспортных средств этот подход может слегка меняться. Это зависит от конечного результата, необходимого для достижения, к примеру, дрифт, быстрая скорость, правильное вхождение в поворот на большой скорости с непростым дорожным покрытием. Но такие параметры совсем не играют роли для автомобилистов, которые управляют машинами на городских дорогах или загородных трассах.

Видео:Физика - движение по окружностиСкачать

Парадокс колеса

На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.

В то же время из школьного курса математики известно, что длина окружности равна:

Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.

Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:

C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.

Но на самом деле она проходит фактически путь вдвое больший.

Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.

Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.

Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.

Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.

Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:

V = w*R, где w — угловая скорость вращения колеса.

Фактически линейная скорость внутренних точек колеса должна описываться уравнением:

V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.

Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.

Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.

Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:

dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R

Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.

С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.

Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.

[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.

Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.

Сазонов Сергей 3 сентября 2019 года в 12:54

Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет.
(конец цитаты)

К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.

Видео:Урок 88 (осн). Линейная скорость точки на вращающемся телеСкачать

Новое в блогах

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

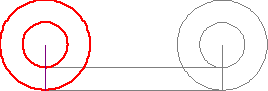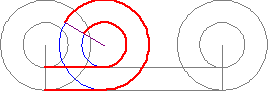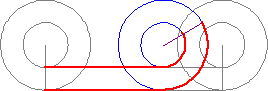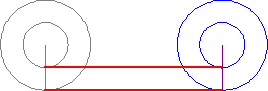
Парадокс Аристотеля о движении двух колес

Имеем два колеса разного размера, расположенных одно в другом. Оба колеса синхронно катятся и проходят определённое расстояние. Смысл парадоксе ясен из картинки: два скрепленных колеса разного радиуса проходят тот же путь при полном обороте.

Если вы внимательно посмотрите на гифку вверху, то заметите – оба колеса полностью совершают оборот по всей своей окружности, чтобы преодолеть одно и то же расстояние (см. на красную линию). А также очевидно, что одна окружность меньше другой. Это означает, что, либо колёса имеют одинаковую окружность (что в корне неверно), либо разные окружности «разворачиваются» на одинаковую длину (чего быть никак не может).

А если представить, что всё это правда? Тогда технически возможно, что колесо с окружностью в 2,54 сантиметра в состоянии пройти тот же путь за один оборот, что и колесо с окружностью, равной 1,6 километров.

Но такого просто не бывает. Длина окружности с меньшим радиусом не может быть равна длине окружности с большим радиусом. Так в чём же дело?