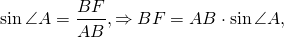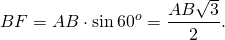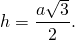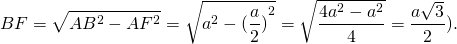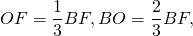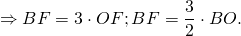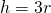В данной публикации мы рассмотрим основные свойства высоты в равностороннем (правильном) треугольнике. Также разберем пример решения задачи по этой теме.
Примечание: треугольник называется равносторонним, если все его стороны равны.
Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать
Свойства высоты в равностороннем треугольнике
Свойство 1
Любая высота в равностороннем треугольнике одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.
- BD – высота, опущенная на сторону AC;
- BD – медиана, которая делит сторону AC пополам, т.е. AD = DC;
- BD – биссектриса угла ABC, т.е. ∠ABD = ∠CBD;
- BD – серединный перпендикуляр, проведенный к AC.
Свойство 2
Все три высоты в равностороннем треугольнике имеют одинаковую длину.
Свойство 3
Высоты в равностороннем треугольнике в ортоцентре (точке пересечения) делятся в отношении 2:1, считая от вершины, из которой они проведены.
Свойство 4
Ортоцентр равностороннего треугольника является центром вписанной и описанной окружностей.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r (следует из Свойства 3).
Свойство 5
Высота в равностороннем треугольнике делит его на два равных по площади (равновеликих) прямоугольных треугольника.
Три высоты в равностороннем треугольнике делят его на 6 равных по площади прямоугольных треугольников.
Свойство 6
Зная длину стороны равностороннего треугольника его высоту можно вычислить по формуле:
a – сторона треугольника.
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать
Пример задачи
Радиус окружности, описанной вокруг равностороннего треугольника, равняется 7 см. Найдите сторону этого треугольника.
Решение
Как мы знаем из Свойств 3 и 4, радиус описанной окружности составляет 2/3 от высоты равностороннего треугольника (h). Следовательно, h = 7 ∶ 2 ⋅ 3 = 10,5 см.
Теперь остается вычислить длину стороны треугольника (выражение выведено из формулы в Свойстве 6):
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать
Найти высоту равностороннего треугольника по радиусу описанной окружности
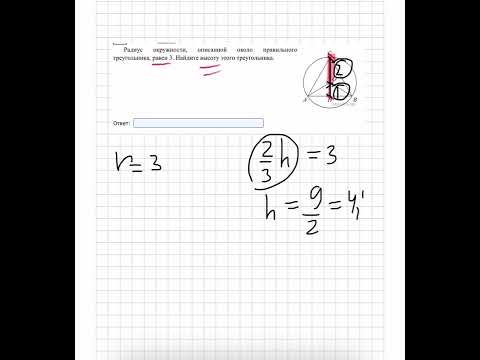
Задание 17. Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Центр описанной около равностороннего треугольника окружности лежит на высоте BH и делит ее в отношении 2:1, считая от вершины B.
В задании нам дана величина радиуса BO=R=12, следовательно, OH=BO:2=6. И вся высота BH=12+6=18.
Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать
Высота равностороннего треугольника
Какими свойствами обладает высота равностороннего треугольника? Как найти высоту равностороннего треугольника через его сторону, радиусы вписанной или описанной окружностей?
(свойство высоты равностороннего треугольника)
В равностороннем треугольнике высота, проведённая к любой стороне, является также его медианой и биссектрисой.
Доказательство :
Пусть в треугольнике ABC AB=BC=AC.
Так как AB=BC, треугольник ABC равнобедренный с основанием AC.
Проведём высоту BF.
По свойству равнобедренного треугольника, BF является также его медианой и биссектрисой
(то есть, AF=FC, ∠ABF=∠CBF).
Аналогично, рассмотрев треугольник ABC как равнобедренный с основанием BC и треугольник ABC — равнобедренный с основанием AB, доказываем, что высоты AK и CD являются также его медианами и биссектрисами
(то есть, BK=KC, ∠BAK=∠CAK; AD=BD, ∠ACD=∠BCD).
Что и требовалось доказать .
(свойство высот равностороннего треугольника)
Все три высоты равностороннего треугольника равны между собой.
Пусть в треугольнике ABC AB=BC=AC.
AK, BF и CD — его высоты.
В прямоугольных треугольниках ABF, BCD и CAK:
гипотенузы AB, BC и CA равны по условию,
∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника).
Следовательно, треугольники ABF, BCD и CAK равны (по гипотенузе и острому углу).
Из равенства треугольников следует равенство соответствующих сторон: BF=CD=AK.
Что и требовалось доказать .
Из теорем 1 и 2 следует, что в равностороннем треугольнике все высоты, медианы и биссектрисы равны между собой.
1) Найдём высоту равностороннего треугольника через его сторону.
В треугольнике ABC AB=BC=AC=a.
Рассмотрим прямоугольный треугольник ABF.
Отсюда формула высоты равностороннего треугольника через его сторону:
(2-й способ: из прямоугольного треугольника ABF по теореме Пифагора
2) Выразим высоту равностороннего треугольника через радиусы вписанной и описанной окружностей.
Точка O — центр правильного треугольника — является также центром его вписанной и описанной окружностей. Как центр вписанной окружности O — точка пересечения биссектрис треугольника. В правильном треугольнике биссектрисы и медианы совпадают. Следовательно, также является O точкой пересечения медиан.
А так как медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины, то BO:OF=2:1, то есть
BO — радиус описанной окружности, OF — вписанной: BO=R, OF=r.
Следовательно, высота равностороннего треугольника равна трём радиусам вписанной окружности:
и в полтора раза больше радиуса описанной окружности:
🔍 Видео
2065 радиус окружности вписанной в правильный треугольник равен 29 Найдите высоту этого треугольникаСкачать
Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать
Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать
Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать
Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать
2050 высота правильного треугольника равна 90 найдите радиус окружностиСкачать
Равносторонний треугольник в окружностиСкачать
ОГЭ ЗАДАНИЕ 16 РАЗДЕЛ ГЕОМЕТРИЯ ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК И ОКРУЖНОСТЬСкачать
Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать
Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать
2053 радиус окружности описанной около правильного треугольника равен 56Скачать
Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать
Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать
Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать
Формулы для равностороннего треугольника.Скачать
Свойство окружности, описанной около равнобедренного треугольникаСкачать
