Найти вектор x коллинеарный вектору a i 2j 2k образующий с ортом (5 видео)

Найти вектор x коллинеарный вектору a i 2j 2k образующий с ортом

α векторы a(2,3,4) и b(3, α,-1) перпендикулярны?

Используя (1.2.7), имеем ab=6+3α -4=0 или 3α =-2 , α =-2/3

Пример1.2.5.При каких значениях α и β векторы а(2,4,α) и b(4,β,1)коллинеарны?

Используя условие коллинеарности векторов (1.2.8), имеем: 2/4=4/β=α/1. Откуда 4/β =1/2 или α/1=1/2, β = 8, а α =1/2

Пример 1.2. 6. Найти вектор b, коллинеарный вектору a(l,-2,-2) образующий с ортом j острый угол и имеющий длину |b| =15.

Пусть вектор b имеет координаты bx , by, bz, Из условия коллинеарности (1.2.8) имеем b = λа или bx = λаx = λ , by = λаy =-2λ , bz= λаz=-2λ.

По формуле (1.2.6) вычисляем

Откуда |λ|=5 или λ5. Получаем два вектора b; b1 (5,-10,-10) и b2 (-5,10,10). Так угол между вектором b и ортом j острый, то cos(b,j)>0 и координата by>0. Поэтому в качестве вектора b выбираем вектор b2 т.е. b =-5 i+10 j+10k .

4. Векторное произведение векторов.

Необходимо обратить внимание студентов на определение правой и левой троек векторов (рис.1.2.6 и 1.2.7).

Тройка некомпланарных векторов a,b,c называется правой (рис.1.2.6) или левой (рис.1.2.7), если будучи приведены к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой (левой) руки.

Векторным произведением векторов а и b называется вектор с, который обозначается символом с=аb и удовлетворяет следующим трем условиям:

1) вектор с перпендикулярен плоскости векторов а и b;

2)образует с векторами а и b правую тройку;

3)длина вектора с численно равна площади параллелограмма, построенного на векторах а и b, т.е.

Из свойств векторного произведения следует обратить внимание на антикоммутативность, т.е. ab=-ba

Пример 1. 2.7. Вычислить площадь треугольника, построенного на векторах а=2т+п и b = т- п , если |т|=2, |n|=1, (m,n)= π/6

Вычислим векторное произведение векторов a, и b и воспользуемся формулой (1.2.9)

ab =(2т+ п)-(т- n)= 2mт- 2mn+nm-пп =0-3mn-0=-3mn

В декартовом базисе векторное произведение векторов а(аx,аy,аz ) и

b(bx, by ,bz) вычисляется по формуле

Пример1.2.8. Найти координаты вектора b=(bx,by,bz), если он перпендикулярен векторам a1 (2,-3,1) и a2 (1,-2,3) и удовлетворяет условию;

Вектор b перпендикулярен векторам a1 и a2. Поэтому его можнo искать в виде:

Удовлетворим условию b(i + 2j-7k)=10; -7λ -10λ + 7λ =10; -10λ=10, λ=-1.

Таким образом вектор имеет вид: b= 7i+5j+k.

Пример 1.2.9.Вычислить площадь треугольника, вершины которого расположены в точках A(1,2,3), B(2,1,-1), С(3,-1,1).

SΔABC =1/2 |ABxAC|.Вычислим координаты векторов АВ и АС и векторное произведение АВАС .

5.Смешанное произведение трех векторов.

Смешанным произведением трех векторов а,b,с называется число, которое обозначается символом ахb-с (смешанное произведение иногда называют векторно-скалярным).

Если векторы а,b,с некомпланарны, то смешанное произведение аb-с равно объему параллелепипеда, построенного на векторах а,b,с, взятому со знаком «+», если упорядоченная тройка векторов а,b,с-правая, и со знаком «-«, если эта тройка — левая.

Из свойств смешанного произведения трех векторов следует отметить следующие:

1)при круговой перестановке векторов смешанное произведение не меняется, т.е. (aх b) с = (сха) b = (bхс) а;

2)если в смешанном произведении поменять местами два соседних сомножителя, то произведение изменит знак, т.е. (aх b) с = -(ахс) b ;

3) смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны, т.е. условием компланарности векторов является равенство нулю смешанного произведения этих векторов.

Смешанное произведение векторов в декартовом базисе

.Если а(ax, ay, az), b(bx, by, bz,) и с(сx, cy, cz), то

Условие компланарности векторов (1.2.12)

Наиболее распространенные задачи, решаемые при помощи смешанного произведения:

1)найти объем параллелепипеда, построенного на векторах а,b,с:

2) найти объем тетраэдра, построенного на векторах а,b,с:

3) проверить компланарны ли векторы а,b,с, если а х b с=0, то векторы компланарны, если а х b с 0, то векторы некомпланарны;

4)проверить правую или левую тройку образуют векторы а,b,с,

>0 -тройка векторов — правая ,

Тогда sinα >0 и cosα >0, cos2α >0. По формулам (1.4.9) вычисляем

Содержание

Дополнительное задание 7
Найти вектор x коллинеарный вектору a=i-2j-2k образующий с ортом j острый угол и имеющий длину |x|=15
Ответы
🎦 Видео

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Дополнительное задание 7

7.17. В треугольнике ABC дано: = a, = b, точка M — середина стороны BC. Выразить вектор через векторы a и b.

7.18. При каких значениях l векторы 2la и (l 3 — 1)a, (a ¹ o), имеют одинаковое направление?

7.19. При каких значениях x векторы x 3 a и (x 2 — x — 2)a, a ¹ o, противоположно направлены?

7.20. Дано: |a| = 13, |b| = 19, |a + b| = 24. Найти: |a — b|.

7.21. Дано: a ^ b, |a| = 5, |b| = 12. Найти: |a + b| и|a — b|.

7.22. В треугольнике ABC: M — точка пересечения медиан треугольника, = a, = b. Разложить и по векторам a и b.

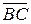
7.23. В параллелограмме ABCD: K и M — середины сторон BC и CD, = a, = b. Выразить векторы и через a и b.

7.24.Проверить, будут ли линейно зависимы векторы l, m, n, разложенные по трем некомпланарным векторам a, b, c: l = a + 2b, m = b +2c, n = c. В случае утвердительного ответа указать связывающую их линейную зависимость.

Ответы к занятию 7

7.2. .

7.3. .

7.4. = , = , = , = .

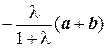
7.5. а) -2; б) — 1; в) ± 1. 7.6. а) да, можно; б) c = 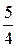m + n.

7.7. Линейно зависимы, 0l — 2m + n = 0.

7.13. а) Линейно независимы; б) линейно независимы;в) линейно зависимы.

7.14. Линейно зависимы; l + m — n = 0. 7.16. l = m = 1. 7.17. .

7.18. (- ¥; 0)È(1; ¥). 7.19. (- ¥; — 1)È(0; 2). 7.20. 22. 7.21. 13; 13.

7.22.3a — b; 2b — 3a. 7.23.2b — 2a. 7.24.Линейно независимы.

Занятие 8. ВЕКТОР В ДекартовЫХ КООРДИНАТАХ

Изучаемый материал: понятие базиса пространства; декартова прямоугольная система координат на плоскости и в пространстве; направляющие косинусы вектора; деление отрезка в данном отношении.

1. Операции с векторами	8.1 — 8.3	8.10 — 8.12	8.19 — 8.21
2. Линейная зависимость. Разложение по базису	8.4 — 8.6	8.13 — 8.15	8.22 — 8.24
3. Геометрические задачи	8.7	8.16	8.25 — 8.27
4. Деление отрезка в данном отношении	8.8, 8.9	8.17, 8.18

Примечание. Для единичного вектора используется обозначение a 0 .

8.1. Заданы векторы a = (– 1, 2, 0), b = (3, 1, 1), c = (2, 0, 1) и d = a – 2b + c.

Вычислить: a) |a| и координаты единичного вектора a 0 вектора a; б) ;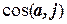

в) координату d_xвектора d; г) пр_j d.

8.2. Найти вектор x, коллинеарный вектору a = i – 2j – 2k, образующий с ортом j острый угол и имеющий длину |x | = 15.

8.3.Найти направляющие косинусы вектора a = (14, 22, 7).

8.4. Являются ли линейно зависимыми следующие системы векторов:

а) (1, 4) и (2, 8); б) (2, – 2, 3) и (4, – 4, 4); в) (3, 2), (6, 4) и (– 12, – 8);

г) (4, 1, 2), (2, 1, 1) и (– 2, 3, – 1).

8.5.Даны три вектора a = (2, – 1), b = (1, 2), c = (4, 3). Найти разложение вектора m = a + b + c по векторам a и b.

8.6. Показать, что тройка векторов a = (1, 0, 0), b = (1, 1, 0), c = (1, 1, 1) образует базис в множестве всех векторов пространства. Вычислить координаты вектора d = –2i – k в базисе (a, b, c) и написать соответствующее разложение по базису.

8.7. Даны две смежные вершины параллелограмма A(– 2, 6), B(2, 8) и точка

пересечения его диагоналей M(2, 2). Найти две другие вершины.

8.8.Даны вершины треугольника A(3, –1, 5), B(4, 2, –5), C(– 4, 0, 3). Найти длину медианы, проведенной из вершины A.

8.9. Определить координаты концов отрезка, который точками

C(2, 0, 2) и D(5, – 2, 0) разделен на три равные части.

Домашнее задание 8

8.10. Заданы векторы a = 2i + 3j, b = – 3j – 2k, c = i + j – k. Найти:

a) координаты единичного вектора ;

б) координаты вектора a – 0,5b + c;

в) разложение вектора a + b – 2c по базису (i, j, k);

г) пр_j (a – b).

8.11. Найти вектор x, образующий со всеми тремя базисными ортами равные острые углы, если |x | = 2 .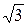

8.12. Найти направляющие косинусы вектора a = (13, – 6, 18). .

8.13. Являются ли линейно зависимыми следующие системы векторов:

а) (1, 4) и (2, 5); б) (2, – 2, 3) и (6, – 6, 9); в) (3, 2), (6, 4) и (– 12, 8);

г) (5, 2, 1), (– 1, 2, 3) и (1, – 1, 3).

8.14. Даны три вектора a = (2, – 1), b = (1, 2), c = (4, 3). Найти разложение вектора m = a + b + c по векторам b и c.

8.15.На плоскости заданы векторы a = (– 1, 2), b = (2, 1) и c = (0, – 2). Убедиться, что (a, b) — базис в множестве всех векторов на плоскости. Построить заданные векторы и найти разложение вектора c по базису (a, b).

8.16. Даны три вершины A(3, – 4, 7), B(– 5, 3, – 2), C(1, 2, – 3) параллелограмма ABCD. Найти его четвертую вершину D, противоположную вершине B.

8.17. На оси ординат найти точку M, равноудаленную от точек A(1, – 4, 7) и

8.18. Отрезок с концами в точках A(3, – 2) и B(6, 4) разделен на три равные части. Найти координаты точек деления.

Видео:2 37 Нахождение орта вектораСкачать