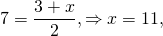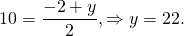Найти уравнение образа окружности при осевой симметрии (3 видео)

Симметричные окружности

Как найти уравнение окружности, симметричной данной?

Симметричные окружности имеют равные радиусы. Следовательно, остаётся найти координаты центра симметричной окружности (как точки, симметричной данной).

1) Окружность задана уравнением (x-3)²+(y+2)²=16. Составить уравнение окружности, симметричной данной относительно точки (7; 10).

Центр окружности (x-3)²+(y+2)²=16 — точка с координатами (3;-2). Найдём точку, симметричную ей относительно точки (7; 10).

Таким образом, центр окружности, симметричной данной, — точка с координатами (11;22). Подставляем в формулу уравнения окружности a=11, b=22, R²=16:

2) Окружность задана уравнением (x+5)²+(y+1)²=9. Составить уравнение окружности, симметричной данной относительно начала координат.

Центром данной окружности является точка (-5;-1). Точка, симметричная данной относительно начала координат — (5;1). Таким образом, для окружности, симметричной данной относительно точки O(0;0) a=5, b=1, R²=9:

3) Окружность задана уравнением (x-7)²+(y-2)²=12. Составить уравнение окружности, симметричной данной относительно прямой y=x.

Центр окружности (x-7)²+(y-2)²=12 — точка (7;2) — при симметрии относительно прямой y=x переходит в точку (2;7). Следовательно, a=2, b=7, R²=12 и искомое уравнение окружности:

4) Окружность задана уравнением (x+4)²+(y-5)²=19. Составить уравнение окружности, симметричной данной относительно прямой y=2x+4.

Центр окружности (x+4)²+(y-5)²=19 — точка (-4;5). Точку, симметричную точке (-4;5) относительно прямой y=2x+4, нашли в прошлый раз — (3,2; 1,4). Таким образом, a=3,2, b=1,4, R²=19 и уравнение симметричной окружности

5) Окружность задана уравнением (x+8)²+(y+3)²=4. Составить уравнение окружности, симметричной данной относительно прямой y= -1.

Центр окружности (x+8)²+(y+3)²=4 — (-8; -3). Точка, симметричная точке (-8; -3) относительно прямой y= -1, имеет такую же абсциссу, x= -8. Расстояние от точки (-8; -3) до прямой y= -1 равно -1-(-3)=2. Расстояние от прямой y= -1 до центра симметричной окружности также равно 2, отсюда -1+2=1 — это ордината центра. Таким образом, точка (-8; 1) — центр окружности, симметричной данной, а R²=4.

Следовательно, искомое уравнение окружности

Содержание

Метод осевой симметрии
Осевая и центральная симметрия
Что такое симметрия
Осевая симметрия
Центральная симметрия
Задачи на самопроверку
🔍 Видео

Видео:Составить уравнение образа окружности при осевой и центральной симметрии. Геометрия 9 классСкачать

Метод осевой симметрии

Этот метод заключается в том, что, проведя анализ задач, замечают, что вместо искомой фигуры можно построить фигуру, симметричную ей относительно некоторой прямой, а затем от нее перейти к построению искомой фигуры, проведя повторную симметрию.

При решении задач на построение методом осевой симметрии надо владеть следующими умениями:

1) строить образы фигур при осевой симметрии;
2) видеть симметричные относительно прямой точки на симметричных относительно этой же прямой фигурах;
3) строить ось симметрии;
4) находить симметричные относительно прямой точки на произвольных заданных фигурах.

Перейдем к решению задач.

Задача 6.6. Построить треугольник наименьшего периметра, вписанный в данный острый угол так, чтобы две его вершины принадлежали сторонам угла, а третья — данной точке внутренней области угла.

Приведем лишь краткие рекомендации по решению предложенной задачи. Решение задачи основано на свойствах осевой симметрии.

Строим точки М_у и М₂, симметричные данной точке М относительно прямых, содержащих стороны этого угла. Точки пересечения отрезка М_УМ₂ со сторонами угла являются вершинами искомого треугольника. Периметр полученного треугольника равен длине отрезка М_УМ₂, периметр любого данного треугольника, одной из вершин которого является точка М, а две другие принадлежат сторонам данного угла, равен длине ломаной, соединяющей точки М_] и М₂.

Задача 6.7. Даны две окружности и прямая I (рис. 6.6). Построить равносторонний треугольник так, чтобы две его вершины принадлежали данным окружностям, а одна из высот — прямой I.

Предположим, что ААВС искомый (см. рис. 6.6).

Так как высота AD равностороннего ДАВС принадлежит прямой I, то точки В и С симметричны относительно этой прямой и лежат на данных окружностях.

Если точка С принадлежит окружности Р₂ и симметрична точке В, принадлежащей окружности F,, относительно прямой I, то точка С принадлежит также и образу окружности F, при симметрии относительно прямой I. Следовательно, точка С есть общая точка окружности F₂ и образа окружности F_y при симметрии S₍. Построить окружность F<, являющуюся образом окружности F_y.

Затем строим точку В как образ точки С при симметрии S,, учитывая, что С принадлежит окружности F <и F_y симметрична F<.

Итак, последовательность построений такова:

1) строим образ окружности F_x при симметрии S,;
2) находим точки пересечения окружностей F <и р 2>
3) отыскиваем на окружности F_x прообразы точек пересечения окружностей F <и F₂;
4) строим равносторонний ААВС (А е I).

Заметим, что задача может иметь единственное решение, когда окружность F₂ пересекает окружность F <в точке С; она может иметь два решения, когда окружности F₂ и F <пересекаются в точках М и К; бесконечно много решений задача имеет тогда, когда окружности F₂ и F <совпадают; задача не имеет решений, когда окружности F₂ и F< не пересекаются.

Задача 6.8. Окружность F_x пересекает концентрические окружности F₂ и F₃ соответственно в точках Л, В и С, D. Доказать, что хорды АВ и CD параллельны.

Пусть О — центр окружности F_x и О_х — центр окружностей F₂ и F₃. И пусть окружности F_x и F₂ пересекаются в точках А и В, а окружности F, и F₃ — в точках С и D. Тогда ОО_х — ось симметрии фигуры F, которая есть объединение окружностей F_x, F₂ и F₃.

Аналогично S_GOl (C) = D. Так как AB J. 00_x и CD 1 00_х, то АВ || CD.

Задача 6.9. На бесконечной прямой АВ найти такую точку С, чтобы полупрямые CM, CN, проведенные из С через данные точки М и N, расположенные по одну сторону АВ, составляли с полупрямыми СА и СВ равные углы.

Анализ. Допустим, что задача решена (рис. 6.7) и

Если повернем этот чертеж на 180° около оси АВ, то отрезок СМ примет положение СМ₂ причем окажется, что

Из равенств (*) и (**) вытекает, что ZACM₂ = ZBCN, т.е. M₂CN — прямая линия. Если удастся построить эту прямую M₂N, то тем самым определим положение искомой точки С, потому что прямая M₂N пересекает прямую АВ именно в этой точке.

Стремясь построить прямую M₂N, нужно принять во внимание, что одна из ее точек (ЛГ) нам дана, а другая (М₂) симметрична точке М относительно оси АВ.

Построение. 1. Из точки М опустим перпендикуляр ММ, на прямую АВ.

2. На продолжении отрезка ММ_Х от точки М, отложим отрезок MjM₂, равный ММ], и получим точку М₂, симметричную точке М относительно оси АВ.
3. Соединим точки М₂ и N.

Отрезок M₂N пересечет прямую АВ в искомой точке С.

Доказательство предлагаем провести читателю самостоятельно.

Исследование. Задача всегда имеет решение. Отметим два частных случая.

1. Если точки М и N не совпадают и находятся на одинаковом расстоянии от прямой АВ, то искомую точку С можно найти иным путем: из середины отрезка MN опустить перпендикуляр на прямую АВ. Основание этого перпендикуляра будет искомой точкой.
2. Если точки М и N лежат на некоторой прямой DE, перпендикулярной к АВ, то точка С есть пересечение линий DE и АВ.

Задача 6.10. Построить по четырем сторонам (a, b, с, d) четырехугольник ABCD, зная, что его диагональ АС делит угол А пополам.

Анализ. Допустим, что ABCD есть искомый четырехугольник (рис. 6.8).

Так как диагональ АС делит угол А пополам, то, отложив на прямой АВ от точки А отрезок AD_b равный AD, мы получим точку D_1; симметричную точке D.

Соединив точки С и D_lt получим отрезок CD_X, равный CD, и ABCD₁.

В Л BCD, нам известны все три стороны: 1) ВС = Ъ, 2) CD₁ = CD = с, 3) BD₁=AD₁-AB=AD -AB = d-a.

Построив ABCD_X по трем сторонам (Ь, с и d — а), можно найти положение точки А: для этого надо на отрезке D_XB от точки D_x отложить отрезок D_XA, равный d. Соединив точки А и С, получим ААВС. Если на стороне АС построить, как показано на рис. 6.8, AACD, равный треугольнику ACD_b то и получим искомый четырехугольник ABCD.

Построение. 1. Строим ABCD _х по трем сторонам: Ъ, end — а.

2. На продолжении стороны BD_X, равной d — а, откладываем от точки Dj отрезок DjA, равный d.
3. Из точки А описываем дугу радиусом, равным d, а из точки С описываем дугу радиусом, равным с, и точку (D) пересечения этих дуг соединяем с точками А и С. ABCD — искомый четырехугольник.

Доказательство предлагаем провести читателю самостоятельно.

Исследование. Как видим, для получения искомого четырехугольника надо сначала построить вспомогательный д.BCD_V стороны которого равны отрезкам Ь, с и d — а. Если сумма любых двух из этих отрезков больше третьего, то искомый четырехугольник можно построить.

От нашего усмотрения зависит, какой из четырех отрезков, данных в условии задачи, принимать за отрезок d, какой — за отрезок а и т.д. Поэтому для выяснения вопроса о числе решений всегда надо рассмотреть все возможные случаи распределения четырех данных отрезков.

Видео:Осевая симметрия. 6 класс.Скачать

Осевая и центральная симметрия

О чем эта статья:

Видео:Осевая и центральная симметрия, 6 классСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Ось симметрии угла — биссектриса.
Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
Оси симметрии прямоугольника проходят через середины его сторон.
У ромба две оси симметрии — прямые, содержащие его диагонали.
У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:Уравнение окружности (1)Скачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
С другой стороны прямой отложим такие же расстояния.
Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
Измеряем расстояние от вершин до точек на прямой.
Откладываем такие же расстояния на другой стороне оси симметрии.
Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Проводим через точку А прямую, перпендикулярную прямой l.
Проводим через точку В прямую, перпендикулярную прямой l.
Измеряем расстояния от точек А и В до прямой l.
Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:48. Осевая и центральная симметрииСкачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Измеряем расстояние от точки B до точки О и от точки А до точки О.
Проводим прямую из точки А через точку О и выводим ее на другую сторону.
Проводим прямую из точки B через точку О и выводим ее на другую сторону.
Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.