Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
- Двумерный случай: многоугольники
- Центр масс системы точек
- Центр масс каркаса
- Центр масс сплошной фигуры
- Случай треугольника
- Случай треугольника: доказательство
- Случай многоугольника
- Случай многоугольника: альтернативный способ
- Трёхмерный случай: многогранники
- Центр масс системы точек
- Центр масс каркаса многогранника
- Центр масс поверхности многогранника
- Центр масс сплошного многогранника
- Случай тетраэдра
- Случай произвольного многогранника
- Нахождение центра масс треугольника
- Центр тяжести треугольника
- 🎦 Видео
Видео:Центр тяжести треугольникаСкачать

Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где 


В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке 

и, выражая отсюда 
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где 




Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник 
Четыре получившихся треугольника подобны треугольнику 

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого 


Пусть теперь вектор 





Наша цель — показать, что вектора 

Обозначим через 






Искомый центр масс 




Таким образом, вектор от вершины 





Таким образом, мы доказали, что вектора 



Более того, попутно мы доказали, что центроид делит каждую медиану в отношении 
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где 



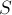
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники 

Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка 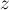


где 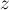




Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении 
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
Видео:Видеоурок 3. Определение центра тяжести.Скачать

Нахождение центра масс треугольника
Любите ли вы геометрию? Многие на этот вопрос отвечают «нет», потому что в школе она даётся труднее всего. Причём особенную нелюбовь вызывают у учеников задачи о пересекающихся отрезках в треугольнике, к которым трудно даже подступиться. В этой статье мы расскажем о замечательном методе решения подобных задач — методе масс.
Эта статья была опубликована в журнале OYLA №10(38). Оформить подписку на печатную и онлайн-версию можно здесь.
Наверняка в детстве вы качались на качелях-весах. И наверняка один из двоих чаще всего оказывался тяжелее и его сторона постоянно перевешивала. А что можно сделать в этой ситуации, чтобы уравновесить качели?
Вспоминаем правило рычага: чтобы система была в равновесии, моменты сил, действующих на качели, должны быть одинаковыми.
Так как силы в нашем случае — это силы тяжести, верно следующее равенство:
Сокращаем константу g и получаем, что отношение масс обратно пропорционально отношению расстояний от края качелей до опоры.
Обратите внимание: вес самих качелей мы не учитываем. То есть система состоит из двух точек — концов отрезка с «гирьками», а также третьей точки, которая делит этот отрезок в отношении, обратно пропорциональном отношению масс «гирек». Последняя точка имеет своё название — она является центром масс системы из двух точек-«гирек».
Что же такое центр масс, или, как его ещё называют, центр тяжести? Формальное определение звучит так:
Точка О называется центром масс системы из n точек А1, А2, …, Аn, где каждой точке соответствует масса m1, m2, …, mn, если верно следующее равенство:
Не пугайтесь этой формулы! На деле решать задачи данным методом можно не думая про векторы. Сделаем допущение, что груз на концах отрезков не имеет размера — только массу.
Чтобы найти центр масс системы из двух точек, надо всего лишь разбить отрезок в отношении, обратно пропорциональном массам точек. Это условие делает верным наше векторное равенство.
Теперь рассмотрим систему из трёх точек, образующих некий треугольник. Как найти его центр масс? Для большей наглядности представим большой поднос, на котором произвольно расставлены гири. И официанта, который ловко удерживает поднос на одном пальце. Точка, в которой палец соприкасается с подносом, и есть центр масс. Только условимся, что поднос обладает бесконечно малой массой.
Как же найти эту точку? Оказывается, у центра масс есть следующее полезное свойство.
Если есть система точек с массами в них и какую-то пару точек А(mA) и B(mB) мы заменим их центром масс Р(mA+mB), то центр масс исходной системы не изменится.
Доказать это свойство попробуйте самостоятельно: это несложное упражнение на векторы.
Давайте применим указанное свойство к треугольнику. Если есть треугольник с вершинами А, В, С с массами в них, то, чтобы найти центр масс данной системы, можно сперва найти центр масс точек А и В (точку Р), а затем найти центр масс точек Р и С. В каждом из двух случаев центр масс мы находим с помощью обычного правила рычага.
Всё это здорово, но возникает резонный вопрос: а зачем? Какое отношение имеют эти рассуждения к геометрическим задачам? Терпение, друзья!
Дан треугольник АВС. М — середина АВ, точка К лежит на отрезке АС и делит его в отношении 1:2 от вершины А. В каком отношении отрезок СМ делит отрезок ВК?
Решение Суть нашего метода в следующем. Расставим в точки А, В и С массы 2, 2 и 1 соответственно. Как вы видите, центр масс точек А(2) и В(2) — это точка М(4). Значит, центр масс всей системы из трёх точек находится на отрезке СМ и делит его в отношении 1:4 от С.
Теперь вернёмся к началу и найдём центр масс точек А и С. Это будет точка К(3). Значит, центр масс исходной системы лежит на отрезке ВК и делит его в отношении 3:2 от В.
Но речь идёт об одной и той же системе точек А, В и С, а значит, у них один и тот же центр масс, который лежит и на СМ, и на ВК. Таким образом, центр масс не что иное, как точка О. Отсюда следует, что искомое отношение ВО к ОК равно 3:2.
Ответ. 3:2.
Постойте-ка! А как это мы догадались расставить массы именно так: 2, 2 и 1? На самом деле никакой магии тут нет. Наша цель — расставить массы в вершинах треугольника так, чтобы их центром оказалась точка О. Но почему именно 2, 2 и 1? Всё дело в том, что О будет центром масс, если мы покажем, что центр масс одновременно лежит и на отрезке СМ, и на отрезке ВК. Следовательно, в первом случае массы из точек А и В должны сместиться в точку М. Вспоминаем правило качелей: так как АМ = ВМ, то массы в точки А и В надо ставить одинаковые. Запомним это.
Во втором случае мы должны поставить массы в А и С так, чтобы их центром была точка К. Но АК:СК = 1:2, значит, в точке А масса должна быть вдвое больше, чем в С. Следовательно, ставим в С массу 1, тогда в А будет 2 (вдвое больше) и в В — тоже 2 (как в А).
Методом масс можно не только решать задачи, но и доказывать теоремы.
Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин.
Решение Рассмотрим медианы ВК и СМ. В данном случае и К, и М — середины, поэтому поставим во все три вершины А, В и С массу 1. Далее рассмотрим точки А и В. Их центр масс — точка М(2). Значит, центр масс системы точек А, В и С лежит на отрезке СМ и делит его в отношении 2:1 от вершины С.
Теперь рассмотрим точки А и С, их центр масс — точка К(2). Значит, центр масс всё той же системы точек А, В и С лежит на отрезке ВК и делит его в отношении 2:1 от вершины В. Но тогда искомый центр масс — это точка О на пересечении отрезков ВК и СМ, причём каждый из отрезков эта точка делит в отношении 2:1 от вершин.
Осталось заметить, что если мы рассмотрим медианы ВК и АР, то их точка пересечения также будет центром масс и разделит ВК и АР в отношении 2:1 от вершин. Но точка, которая делит ВК в отношении 2:1 от В, единственная, значит, в обоих случаях речь идёт об одной и той же точке О. Итак, все три медианы проходят через точку О и делятся ею в отношении 2:1 от вершин, что и требовалось доказать.
Видео:Центр тяжестиСкачать

Центр тяжести треугольника
Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин
Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.
Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.
🎦 Видео
Найдите центр тяжестиСкачать

Механика | динамика | центр масс треугольникаСкачать

координаты центра тяжести треугольникаСкачать

Центр тяжести. ЭкспериментСкачать

Центры тяжести прямоугольных треугольниковСкачать
Определение центра тяжести плоской фигуры. Подробное объяснение. Сопромат для чайниковСкачать

Определение центра тяжести сложной фигуры. СопроматСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

"ПО ФАКТАМ" с Юлией Федоровой. 17.01.2024Скачать

Урок 80. Определение положения центра масс телаСкачать

Практическая №5 Определение центра тяжести сложной фигурыСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Как найти центр тяжести любой фигуры?Скачать

97 Медианы и центр тяжести треугольникаСкачать

Центр масс в математике (или механика помогает геометрии)Скачать

Практическая работа по теме: Центр тяжестиСкачать




















