Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- Окружность, вписанная в треугольник
- Определение окружности, вписанной в треугольник
- Теорема об окружности, вписанной в треугольник
- Вписанная и описанная окружности
- Вписанная окружность
- Теорема 1 (об окружности, вписанной в треугольник)
- Готовые работы на аналогичную тему
- Описанная окружность
- Теорема 2 (об окружности, описанной около треугольника)
- Пример задачи на понятия вписанной и описанной окружности
- 📽️ Видео
Видео:Окружность, вписанная в треугольникСкачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
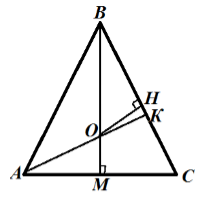
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
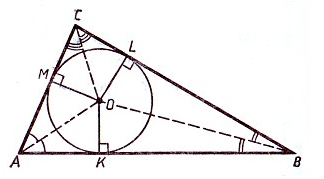
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
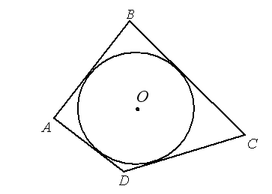
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||||
| Произвольный треугольник | ||
 | ||
| Равнобедренный треугольник | ||
 | ||
| Равносторонний треугольник | ||
 | ||
| Прямоугольный треугольник | ||
 | ||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Окружность, вписанная в треугольник
Видео:Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Определение окружности, вписанной в треугольник
Определение 1. Окружностью, вписанной в треугольник называется окружность, которая находится внутри треугольника и касается всех его сторон (Рис.1).
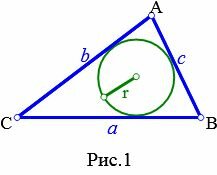 |
Можно дать и другое определение окружности, вписанной в треугольник.
Определение 2. Окружностью, вписанной в треугольник называется наибольшая окружность, которая может находится внутри треугольника.
При этом треугольник называется треугольником описанным около окружности . Центр вписанной в треугольник окружности явлется точка пересечения биссектрис треугольника. Центр окружности вписанной в треугольник называется инцентром треугольника.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Теорема об окружности, вписанной в треугольник
Теорема 1. В любой треугольник можно вписать окружность.
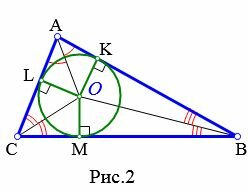 |
Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения биссектрис треугольника. Проведем из точки O перпендикуляры OK, OL и OM к сторонам AB, AC, BC, соответственно. Поскольку точка O равноудалена от сторон треугольника ABC, то OK=OL=OM. Тогда окружность с центром O и радиусом OK проходит через три точки K, L, M. Стороны AB, AC, BC треугольника ABC касаются этой окружности в точках K, L, M, поскольку они перпендикулярны к радиусам OK, OL, OM, соответственно. Следовательно, окружность с центром O и радиусом OK является вписанной в треугольник ABC.
Замечание 1. В любой треугольник можно вписать только одну окружность.
Доказательство. Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из этих окружностей равноудален от сторон треугольника и совпадает с точкой O пересечения биссектрис треугольника. Радиус этих окружностей равен расстоянию от точки O до сторон треугольника. Поэтому эти окружности совпадают.
Видео:Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

Вписанная и описанная окружности
Вы будете перенаправлены на Автор24
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанная окружность
Если все стороны многоугольника являются касательными одной окружности, то такая окружность называется вписанной в многоугольник (рис 1).
Многоугольник, удовлетворяющий условию определения 1, называется описанным около окружности.
Рисунок 1. Вписанная окружность
Видео:ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать

Теорема 1 (об окружности, вписанной в треугольник)
В любой треугольник можно вписать окружность и притом только одну.
Доказательство.
Рассмотрим треугольник $ABC$. Проведем в нем биссектрисы, которые пересекаются в точке $O$ и проведем из нее перпендикуляры на стороны треугольника (Рис. 2)
Рисунок 2. Иллюстрация теоремы 1
Существование: Проведем окружность с центром в точке $O$ и радиусом $OK. $Так как точка $O$ лежит на трех биссектрисах, то она равноудалена от сторон треугольника $ABC$. То есть $OM=OK=OL$. Следовательно, построенная окружность также проходит через точки $M и L$. Так как $OM,OK и OL$ — перпендикуляры к сторонам треугольника, то по теореме о касательной к окружности, построенная окружность касается всех трех сторон треугольника. Следовательно, в силу произвольности треугольника, в любой треугольник можно вписать окружность.
Готовые работы на аналогичную тему
Единственность: Предположим, что в треугольник $ABC$ можно вписать еще одну окружность с центром в точке $O’$. Её центр равноудален от сторон треугольника, а, следовательно, совпадает с точкой $O$ и имеет радиус, равный длине $OK$. Но тогда эта окружность совпадет с первой.
Теорема доказана.
Следствие 1: Центр вписанной в треугольник окружности лежит в точке пересечения его биссектрис.
Приведем еще несколько фактов, связанных с понятием вписанной окружности:
Не во всякий четырехугольник можно вписать окружность.
В любом описанном четырехугольнике суммы противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Описанная окружность
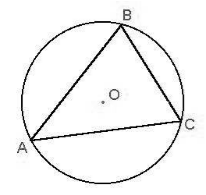
Если на окружности лежат все вершины многоугольника, то окружность называется описанной около многоугольника (Рис. 3).
Многоугольник, удовлетворяющий условию определения 2, называется вписанным в окружность.
Рисунок 3. Описанная окружность
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Теорема 2 (об окружности, описанной около треугольника)
Около любого треугольника можно описать окружность и притом только одну.
Доказательство.
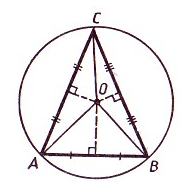
Рассмотрим треугольник $ABC$. Проведем в нем серединные перпендикуляры, пересекающиеся в точке $O$, и соединим ее с вершинами треугольника (рис. 4)
Рисунок 4. Иллюстрация теоремы 2
Существование: Построим окружность с центром в точке $O$ и радиусом $OC$. Точка $O$ равноудалена от вершин треугольника, то есть $OA=OB=OC$. Следовательно, построенная окружность проходит через все вершины данного треугольника, значит, она является описанной около этого треугольника.
Единственность: Предположим, что около треугольника $ABC$ можно описать еще одну окружность с центром в точке $O’$. Её центр равноудален от вершин треугольника, а, следовательно, совпадает с точкой $O$ и имеет радиус, равный длине $OC.$ Но тогда эта окружность совпадет с первой.
Теорема доказана.
Следствие 1: Центр описанной около треугольника окружности совпадает с точкой пересечения его серединных перпендикуляров.
Приведем еще несколько фактов, связанных с понятием описанной окружности:
Около четырехугольника не всегда можно описать окружность.
В любом вписанном четырехугольнике сумма противоположных углов равна $^0$.
Если сумма противоположных углов четырехугольника равна $^0$, то около него можно описать окружность.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Пример задачи на понятия вписанной и описанной окружности
В равнобедренном треугольнике основание равно 8 см, боковая сторона равна 5 см. Найти радиус вписанной окружности.
Решение.
Рассмотрим треугольник $ABC$. По следствию 1, мы знаем, что центр вписанной окружности лежит на пересечении биссектрис. Проведем биссектрисы $AK$ и $BM$, которые пересекаются в точке $O$. Проведем перпендикуляр $OH$ из точки $O$ на сторону $BC$. Изобразим рисунок:
Так как треугольник равнобедренный, то $BM$ и медиана и высота. По теореме Пифагора $^2=^2-^2, BM=sqrt<^2-frac<^2>>=sqrt=sqrt=3$. $OM=OH=r$ — искомый радиус вписанной окружности. Так как $MC$ и $CH$ отрезки пересекающихся касательных, то по теореме о пересекающихся касательных, имеем $CH=MC=4 см$. Следовательно, $BH=5-4=1 см$. $BO=3-r$. Из треугольника $OHB$, по теореме Пифагора, получим:
Ответ: $frac$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 29 03 2022
📽️ Видео
Вписанная и описанная окружность - от bezbotvyСкачать

Задание 24 Радиус окружности вписанной в прямоугольный треугольникСкачать
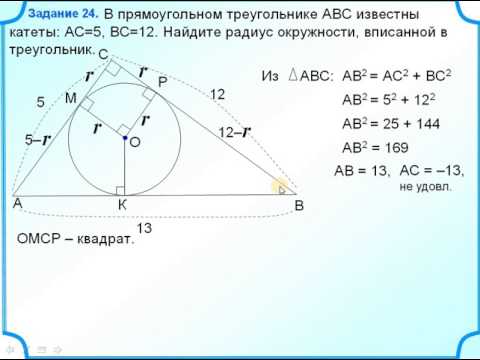
РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Построить окружность, вписанную в треугольникСкачать

Построение окружности, вписанной в треугольникСкачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

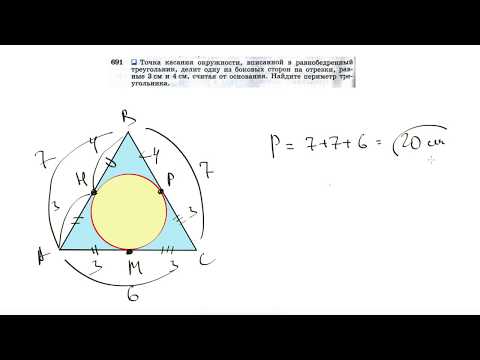
№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать
8 класс, 38 урок, Вписанная окружностьСкачать