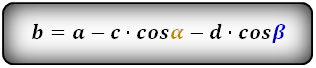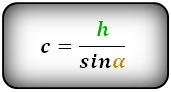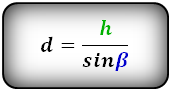Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
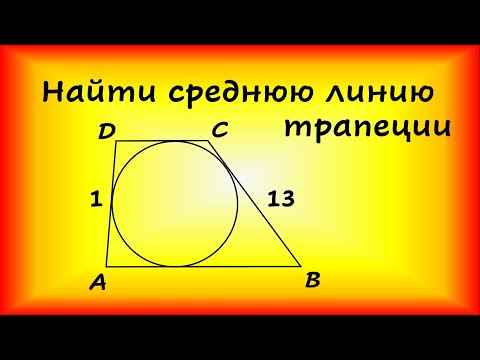
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:Задача про трапецию, описанную около окружностиСкачать

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:Трапеция и вписанная окружностьСкачать

Стороны трапеции
Видео:2113 Боковые стороны трапеции описанной около окружности равны 16 и 3 Найдите среднюю линию трапецииСкачать

Свойства
Трапеция является фигурой с двумя параллельными противоположными сторонами, при этом все четыре стороны могут быть разной длины. Параллельные стороны b и d называются меньшим и большим основанием трапеции, a и c – боковыми сторонами. Зная стороны трапеции, можно найти все характеризующие ее параметры. Периметр трапеции, зная стороны, представляет собой их сумму. P=a+b+c+d
Высота трапеции является перпендикуляром, соединяющим два основания, и может быть проведена в любой их точке, но удобнее всего это делать из вершины углов при меньшем основании, так как тогда образуется прямоугольный треугольник, из которого выводится формула. (рис.103.1) h=√(a^2-(((d-b)^2+a^2-c^2)/2(d-b) )^2 )
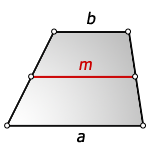
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон, и равный полусумме оснований. (рис.103.2) m=(b+d)/2
Площадь трапеции равна произведению ее высоты на среднюю линию. Чтобы найти площадь трапеции через стороны, необходимо развернуть эту формулу до ее истоков, заменив неизвестные переменные. S=hm=√(a^2-(((d-b)^2+a^2-c^2)/2(d-b) )^2 )*(b+d)/2
Если в трапецию можно вписать окружность (а это возможно, если противоположные стороны в сумме дают одно и то же число), то радиус вписанной окружности будет равен половине высоты, или половине квадратного корня из произведения меньшего основания на большее, с учетом условия для окружности. (рис.103.3) r=h/2=√bd/2
Описать окружность можно только вокруг равнобокой трапеции, и если она является таковой, то радиус описанной окружности будет равен радиусу окружности, описанной вокруг треугольника, образованного диагональю. (рис.103.4) R=(abd_1)/√((a+b+d_1)(a+b)(a+d_1)(b+d_1))
Диагонали трапеции рассчитываются по формулам, приведенным через теорему Пифагора в треугольниках, образованных высотой и диагоналями. d_1=√(c^2+db d(c^2-a^2 )/(d-b)) d_2=√(a^2+db (b(c^2-a^2))/(d-b))
Видео:Радиус описанной окружности трапецииСкачать

Все формулы сторон трапеции
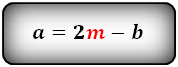
1. Формула длины основания трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
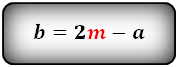
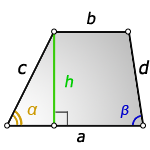
2. Формулы длины сторон через высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
h — высота трапеции
Формулы всех четырех сторон трапеции :
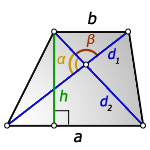
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
d 1 , d 2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
💡 Видео
Трапеция, вписанная в окружностьСкачать

Задание 26_Равнобедренная трапеция. Вписанная окружность.Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Задание 24 ОГЭ по математике #4Скачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать

Как найти стороны равнобокой трапеции, описанной около трёх попарно касающихся равных окружностей?Скачать
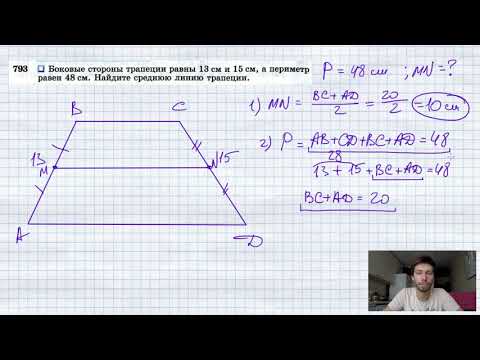
№793. Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линиюСкачать
Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

8 класс, 6 урок, ТрапецияСкачать

Окружность, вписанная в трапециюСкачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать