Найти статические моменты треугольника

Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 206, 207. Рассмотрите внимательно примеры, приведенные в указанных пунктах.

573. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпадал с началом координат, а диаметр, относительно которого мы ищем сгатический момент, совпадал с осью Ох. Тогда статический момент полуокружности относительно диаметра выразится следующей формулой:

В выбранной системе координат уравнение полуокружности запишется так: у —V R2—х. Тогда

574. Найти статические моменты относительно осей Ox и Oy дуги эллипса , расположен

ной в первом квадранте.

Решение. Найдем статический момент дуги эллипса относительно оси Ох. Из уравнения эллипса имеем

(мы берем перед корнем знак , так как по условию кривая расположена в первом квадранте).

Найдем статический момент дуги эллипса относительно оси Oy. Из уравнения эллипса имеем:

X = JLyW=T*-, dl = — L YbUg^ZFldy.

К, -|f VF=V? — j — /езщрг dy=

575. Найти статический момент прямоугольника с основанием а и высотой h относительно его сторон.

Решение. Выберем систему координат так, чтобы ось Ox совпадала с основанием, а начало координат — с прилегающей к основанию стороной. Тогда статический момент плоского тела относительно оси Ox будет вычисляться по формуле:

В нашем случае у = h,

Статический момент относительно оси Oy вычисляется по формуле:

576. Налти статический момент фигуры, представленной на рисунке 23 относительно стороны OD1 если известно, что OA = 3 см, AB = 5 см, BC = 5 см, OF = 8см, а дуга CD есть четвертая часть окружности радиуса CF = FD = S см.

Решение. Как видно из рисунка 23, данная фигура имеет сложную форму. Разобьем это тело на простые геометрические фигуры и применим затем теорему: статический момент фигуры относительно некоторой оси равен сумме статических моментов ее частей относительно той же оси.

Выберем систему координат, как показано на рисунке 23. Легко видеть, что данную фигуру можно рассматривать как сумму дзух трапеций OABM и MBCF и одной четвертой части круга.

Координаты точек At Bt C9 Dy F определить легко: Л (0, 3), В (4, 6), С (8, 3), £>(11, 0), F( 8, 0).

Найдем уравнения прямых AB и BCt как уравнения прямых, проходящих через две данные точки:

уравнение прямой AB:

уравнение прямой ВС:

Так как центр F окружности лежит на оси Ox и отстоит от начала координат на расстоянии OF — 8, то уравнение окружности будет

Учитывая все вышеизложенное, найдем:

577. Найти статический момент тела, ограниченного одной аркой циклоиды относительно оси Ох.

Решение. Так как параметр t для одной арки циклоиды изменяется от 0 до 2я, то

578. Найти момент инерции одной арки циклоиды

Относительно оси Ох. Решение. Как было показано в теоретическом курсе, момент инерции дуги относительно оси Ox вычисляется по формуле:

где —дифференциал дуги. Найдем дифференциал дуги:

579. Найти момент инерции дуги окружности

, лежащей в первом квадранте, относительно

Решение. Как известно, момент инерции кривой относительно оси Oy вычисляется по формуле:

Так как и, следо

Для вычисления Была использована

580. Найти момент инерциифигуры, вграниченной дугой полуокружности Относительно

Решение. Как известно из теоретического курса, момент инерции Ix плоского тела относительно оси Ojc равен:

где dS—элементарная площадь тела.

581. Найти статические моменты дуги параболы у2 = 2х (у > 0) относительно осей Ox и Oy от х = 0 до

582. Найти статический момент дуги астроиды х3 —2_ 2_

— j-y 3 = а 3 , лежащей в первом квадранте, относительно оси Oy.

583. Найти статический момент относительно оси Ox

584. Вычислить статический момент фигур, ограниченных следующими линиями:

COS X OT ТОЧКИ X —до точки

дуги косинусоиды у

а) у —- и у = Xi относительно оси Ох

б) у — X1 и у = Y х относительно оси Ох.

585. Вычислить статический момент фигуры, представленной на рисунке 24, где BC\AD, CKJ_AD, AB = 5, BC = 2, CK = KD = 3, AK = 6, относительно оси Ох.

586. Найти статический момент прямоугольного равнобедренного треугольника с катетом, равным а, относительно этого катета.

587. Найти момент инерции отрезка AB, где А (2; 3), В (5; 4), относительно обеих координатных осей.

588. Найти момент инерции треугольника ABC (рис. 25) относительно стороны Ь.

589. Найти момент инерции прямоугольника со сторонами а и b относительно обеих сторон.

590. Найти момент инерции трапеции ABCD относительно ее основания AD1 если AD=а, BC = 6, высота трапеции равна h.

591. Найти момент инерции

параболического сегмента относительно основания. Основание сегмента равно а, «стрела сегмента» равна А.

Видео:Моменты инерции для треугольника. Вывод моментов инерции для треугольниковСкачать

Центр тяжести

Видео:Статический моментСкачать

Статические моменты площади сечения. Центр тяжести площади сечения

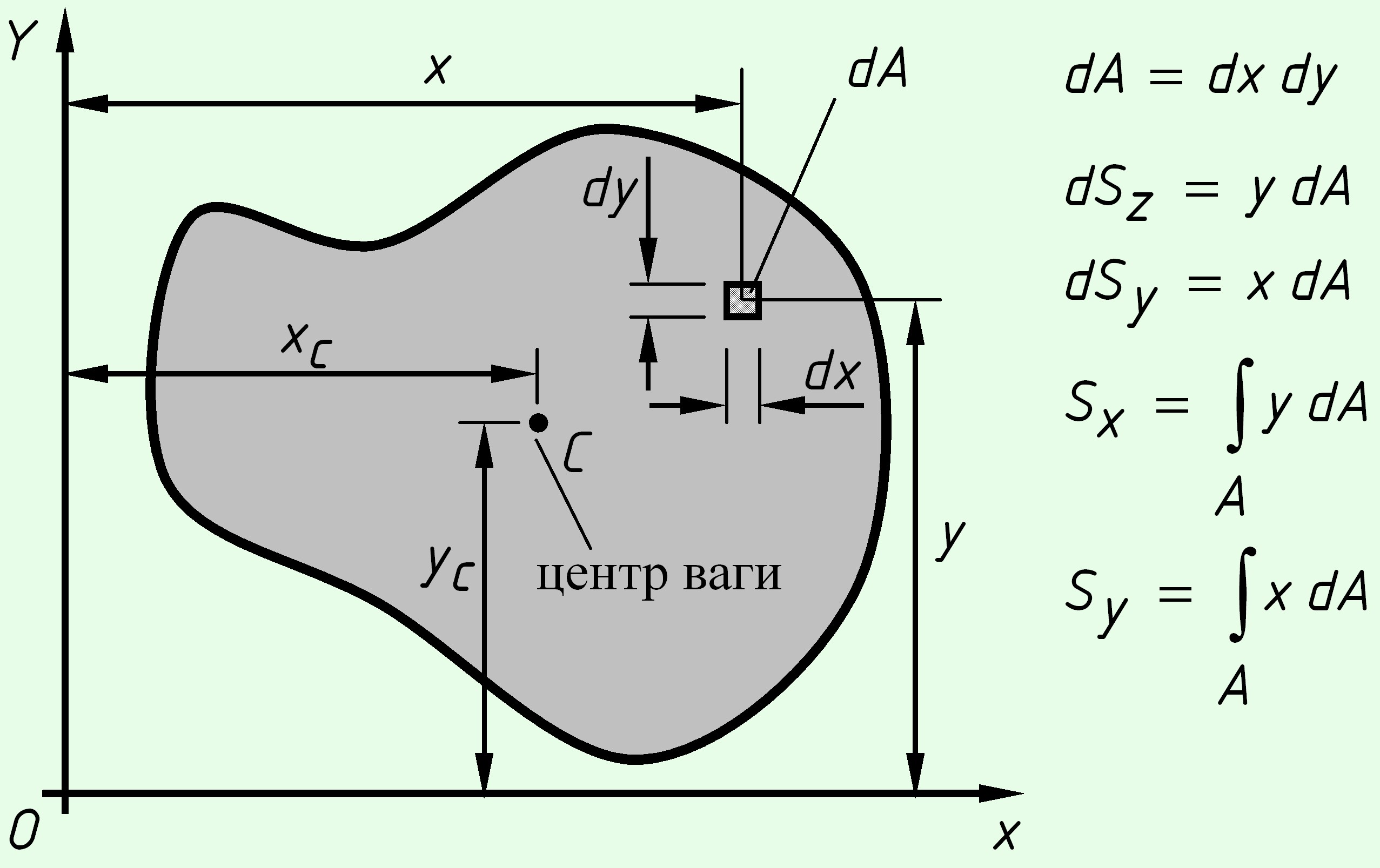
Рассмотрим произвольное поперечное сечение стержня, связанный с координатными осями $XOY$ и выделим элемент площади $dA$ с координатами ($x,y$).

Статическим моментом площади сечения относительно оси называется сумма (интеграл) по всей площади сечения от произведения площади элементарной площадки на расстояние до рассматриваемой оси.

Для сечений, для которых известны площади $A$ и координаты центров тяжести $$, $$, статические моменты площадей рассчитываются по формулам:

Статический момент площади сечения может быть положительным, отрицательным и равняться нулю.

Оси, относительно которых статические моменты площади сечения равны нулю, называются центральными.

Видео:Моменты инерции сечения из простых фигурСкачать

Примеры определения статических моментов

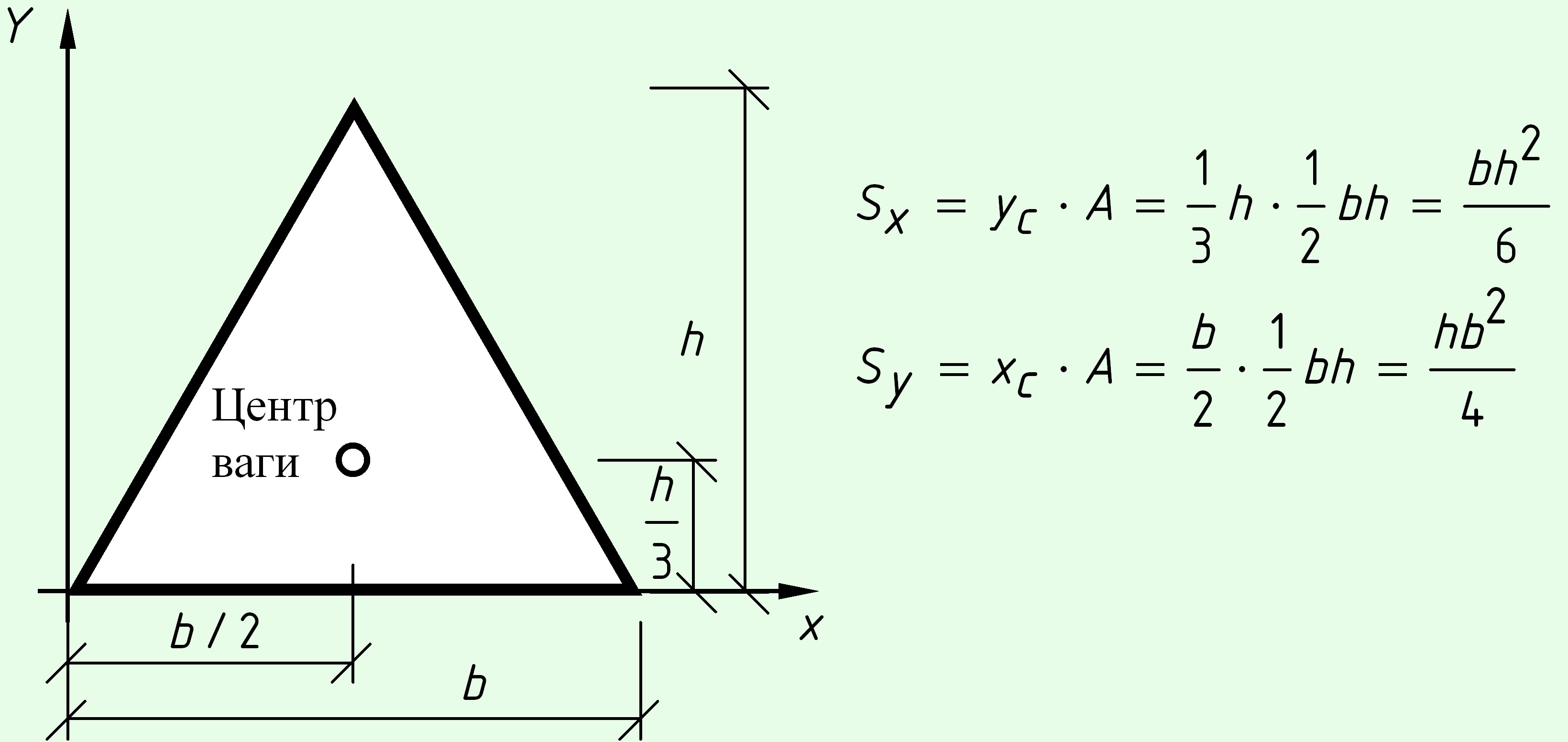
Треугольник.

Поскольку положение центра тяжести треугольника нам известно, его статический момент площади можно определить как произведение площади на соответствующую координату центра тяжести.

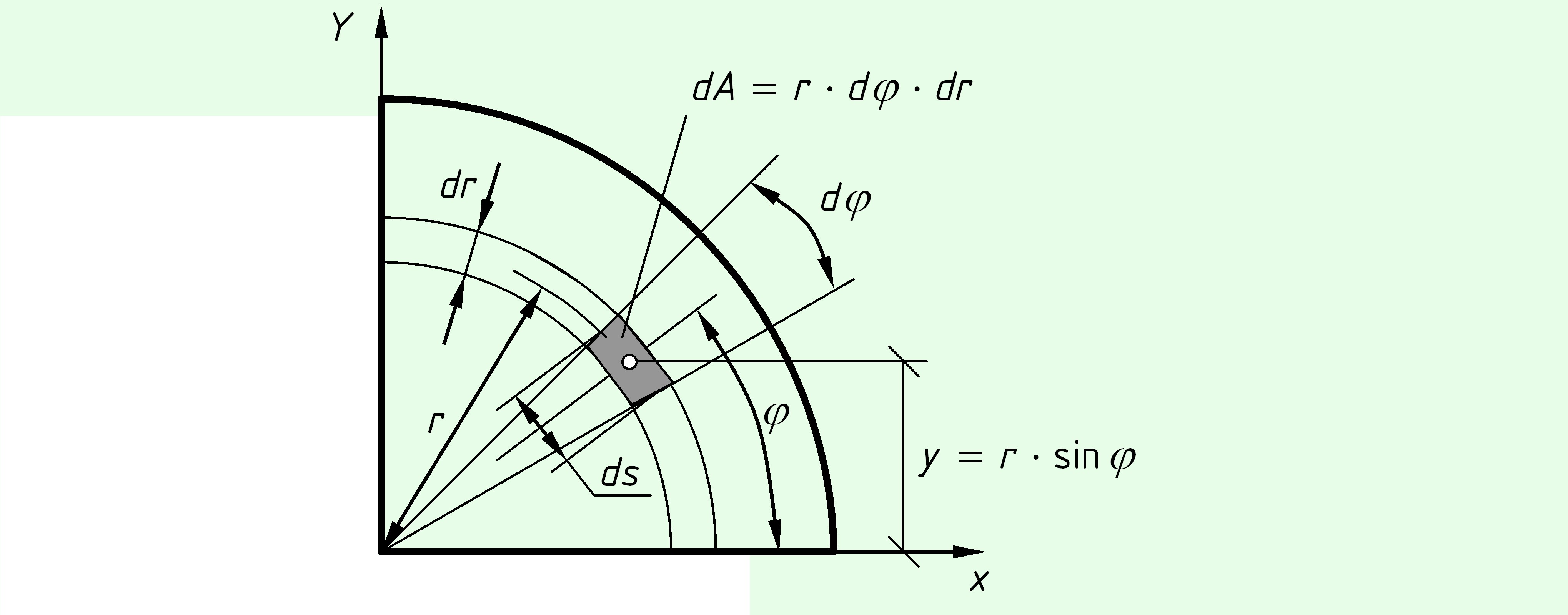
Четверть круга.

Поскольку положение центра тяжести четверти круга мы не знаем, определим статические моменты по общей формуле. Выделим элементарную площадь $dA$ с углом $dvarphi $ и высотой $dr$. Ширина площадки $ds = r cdot dvarphi ,$.

Площадь $A = frac cdot pi $.

Аналогично относительно другой оси $ = frac<<>> = frac<><>$.

Статический момент составного сечения равен сумме статических моментов его составляющих.

Тогда положение центра тяжести составного сечения запишется так:

Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Расчет геометрических характеристик плоских сечений простой формы

Этот онлайн калькулятор рассчитывает статические моменты, моменты инерции и радиусы инерции для плоских сечений простой формы

Данный онлайн калькулятор предназначен для вычисления основных геометрических характеристик простейших сечений. Калькулятор выводит пользователю статический момент, момент инерции и радиус инерции по осям x и y, а также координаты центра тяжести и площадь поперечного сечения. Теорию и формулы расчета можно найти под калькулятором.

Расчет геометрических характеристик плоских сечений простой формы

Левый нижний угол

Правый верхний угол

Центр

Радиус

Вершина при прямом угле

Вторая вершина

Третья вершина

Общий алгоритм расчета следующий:

1. Определение центра тяжести поперечного сечения
2. Определение площади поперечного сечения
3. Определение статического момента
4. Определение осевого момента инерции
5. Определение радиуса инерции

Статический моменты сечения , .

Физический смысл статического момента: если каждую простую фигуру, из которых состоит сложная фигура, наделить весом, то они будут представлять систему параллельных сил и каждая из них станет создавать свой момент относительно какой-либо оси с плечом, равным расстоянию от оси до центра тяжести данной простой фигуры. Если силу заменить площадью, то момент превратится из силового в геометрический показатель, называемый статическим моментом. 1 Измеряется в единицах длины в кубе (см³), может быть положительным, отрицательным и равным нулю.

В общем случае математическая запись статических моментов относительно оси x и y имеет вид:

Для частных случаев, когда рассматриваемая фигура представляет собой простую геометрическую, интегральная запись может быть заменена более простой, тогда формулы выглядят так:

где A — площадь поперечного сечения.
, — расстояние от осей x и y до центра тяжести простой фигуры.

Центр тяжести прямоугольника расположен в точке пересечения его диагоналей. Центр тяжести окружности совпадает непосредственно с центром самой окружности, а нахождение центра тяжести для треугольника можно найти в этом калькуляторе.

Осевой момент инерции

Осевой момент инерции площади сечения — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Величина осевого момента инерции всегда положительна. Формулы для осевого момента инерции:

Момент инерции фигуры относительно оси, проходящей через ее центр тяжести, называется центральным, или собственным, моментом инерции. Если фигура состоит из нескольких простых фигур, то оси, проведенные через центр тяжести всей фигуры, называются главными центральным осями. Моменты инерции относительно главных центральных осей называются главными центральными моментами.

Приведем формулы главных центральных моментов каждого из используемых в калькуляторе простейших сечений

Прямоугольник

1. Площадь поперечного сечения для прямоугольника находится по формуле: ,
   где b и h — стороны прямоугольника.
2. Моменты инерции и для прямоугольника находятся по формулам:

Для иллюстрации вывода формул центральных моментов рассмотрим вывод приведенной выше формулы главного центрального момента инерции для прямоугольника.

Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.
Главный центральный момент инерции относительно оси

Прямоугольный треугольник, катеты которого параллельны осям

1. Площадь поперечного сечения для прямоугольного треугольника находится по формуле: ,
   где b и h — катеты треугольника.
2. Моменты инерции и для треугольника находятся по формулам:

1. Площадь поперечного сечения для круга находится по формуле: ,
   где r — радиус окружности.
2. Моменты инерции и для круга находятся по формулам:

Для нахождения осевого момента инерции относительно произвольной оси воспользуемся теоремой Гюйгенса – Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр тяжести (центрального момента), и произведения площади тела на квадрат расстояния между осями. Измеряется в единицах длины в четвертой степени (см⁴).
Формулы:

Радиус инерции

Радиусом инерции i называют расстояние от соответствующей оси до точки, концентрация всей площади сечения в которой, даст такой же момент инерции, как и для всей площади рассматриваемой фигуры. Измеряется в единицах длины (см).

где A — площадь поперечного сечения,
, — осевые моменты инерции.

Техническая механика для строительных специальностей: учеб. пособие для студ. сред. проф. образования / В.И. Сетков — М.: Издательский центр «Академия», 2007. ↩

📸 Видео

7. Момент инерции треугольника и конусаСкачать

Сопротивление материалов. Лекция: геометрические характеристики сечений - статические моментыСкачать

Статический момент площади сечения (фигуры) относительно осиСкачать

Моменты инерции простейших фигур. Оси центральные и главные. Что это и где. #сопроматСкачать

Основы сопромата. Задача 4. Момент инерции сложного сеченияСкачать

Момент инерцииСкачать

Урок 94. Вычисление моментов инерции телСкачать

Моменты инерции Прямоугольника ► Вывод моментов инерции для прямоугольникаСкачать

Техническая механика | Центр тяжести | Статический момент | Сечение компонентаСкачать

Определение осевых моментов инерции составного несимметричного сечения. СопроматСкачать

Основы Сопромата. Геометрические характеристики поперечного сеченияСкачать

Теория (часть 1) осевые моменты инерцииСкачать

Сопротивление материалов. Лекция: геометрические характеристики сечений - моменты инерцииСкачать

Определение центра тяжести сложной фигуры. СопроматСкачать

Моменты инерции относительно Главных Центральных осей для простых фигурСкачать

Практическое занятие "Геометрические характеристики плоских сечений"Скачать