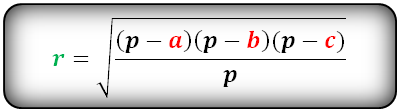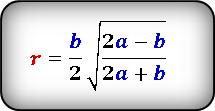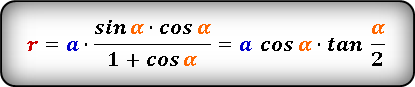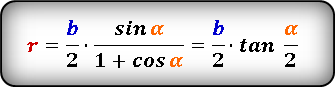Найти радиус вписанной окружности если известен радиус описанной

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

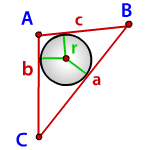
Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

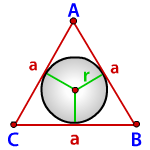
Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

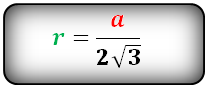
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Видео:Радиус описанной окружностиСкачать

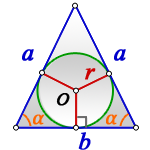
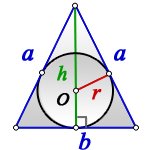
Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Видео:РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Как найти радиус окружности. Вписанная и описанная окружность

Радиус – это отрезок, который соединяет любую точку на окружности с ее центром. Это одна из самых важных характеристик данной фигуры, поскольку на ее основе можно вычислить все другие параметры. Если знать, как найти радиус окружности, то можно рассчитать ее диаметр, длину, а также площадь. В том случае, когда данная фигура вписана или описана вокруг другой, то можно решить еще целый ряд задач. Сегодня мы разберем основные формулы и особенности их применения.

Видео:Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

Известные величины

Если знать, как найти радиус окружности, который обычно обозначают буквой R, то его можно вычислить по одной характеристике. К таким величинам относят:

• длину окружности (C);
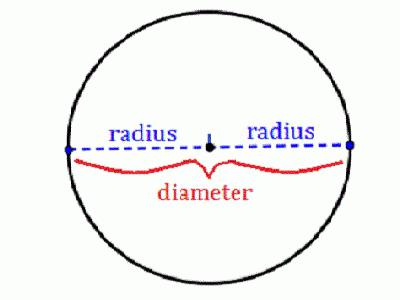
• диаметр (D) – отрезок (вернее, хорда), который проходит через центральную точку;
• площадь (S) – пространство, которое ограничено данной фигурой.

Видео:Разбираем стереометрию за 6 часов | ЕГЭ по математике | Эрик ЛегионСкачать

По длине окружности

Если в задаче известна величина C, то R = С / (2 * П). Эта формула является производной. Если мы знаем, что из себя представляет длина окружности, то ее уже не нужно запоминать. Предположим, что в задаче C = 20 м. Как найти радиус окружности в этом случае? Просто подставляем известную величину в вышеприведенную формулу. Отметим, что в таких задачах всегда подразумевается знание числа П. Для удобства расчетов примем его значение за 3,14. Решение в этом случае выглядит следующим образом: записываем, какие величины даны, выводим формулу и проводим вычисления. В ответе пишем, что радиус равен 20 / (2 * 3,14) = 3,19 м. Важно не забыть о том, что мы считали, и упомянуть название единиц измерения.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

По диаметру

Сразу подчеркнем, что это самый простой вид задач, в которых спрашивается о том, как найти радиус окружности. Если такой пример попался вам на контрольной, то можете быть спокойны. Тут даже не нужен калькулятор! Как мы уже говорили, диаметр – это отрезок или, правильнее сказать, хорда, которая проходит через центр. При этом все точки окружности равноудалены. Поэтому данная хорда состоит из двух половинок. Каждая из них является радиусом, что следует из его определения как отрезка, который соединяет точку на окружности и ее центр. Если в задаче известен диаметр, то для нахождения радиуса нужно просто разделить эту величину на два. Формула выглядит следующим образом: R = D / 2. Например, если диаметр в задаче равен 10 м, то радиус – 5 метров.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

По площади круга

Этот тип задач обычно называют самым сложным. Это связано в первую очередь с незнанием формулы. Если знать, как найти радиус окружности в этом случае, то остальное – дело техники. В калькуляторе только нужно заранее найти значок вычисления квадратного корня. Площадь круга – это произведение числа П и радиуса, умноженного на самого себя. Формула выглядит следующим образом: S = П * R 2 . Обособив радиус на одной из сторон уравнения, можно с легкость решить задачу. Он будет равен квадратному корню из частного от деления площади на число П. Если S = 10 м, то R = 1,78 метров. Как и в предыдущих задачах, важно не забыть об используемых единицах измерения.

Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Как найти радиус описанной окружности

Предположим, что a, b, c – это стороны треугольника. Если знать их величины, то можно найти радиус описанной вокруг него окружности. Для этого сначала нужно найти полупериметр треугольника. Чтобы было легче для восприятия, обозначим его маленькой буквой p. Он будет равен половине суммы сторон. Его формула: p = (a + b + c) / 2.

Также вычислим произведение длин сторон. Для удобства обозначим его буквой S. Формула радиуса описанной окружности будет выглядеть так: R = S / (4 * √(p * ( p — a ) * (p — b) * (p — c)).

Рассмотрим пример задачи. У нас есть окружность, описанная вокруг треугольника. Длины ее сторон составляют 5, 6 и 7 см. Сначала вычисляем полупериметр. В нашей задаче он будет равен 9 сантиметрам. Теперь вычислим произведение длин сторон – 210. Подставляем результаты промежуточных расчетов в формулу и узнаем результат. Радиус описанной окружности равен 3,57 сантиметра. Записываем ответ, не забывая о единицах измерения.

Видео:Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

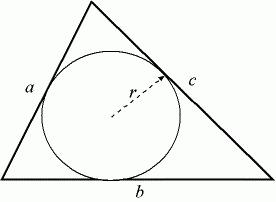
Как найти радиус вписанной окружности

Предположим, что a, b, c – длины сторон треугольника. Если знать их величины, то можно найти радиус вписанной в него окружности. Сначала нужно найти его полупериметр. Для облегчения понимания обозначим его маленькой буквой p. Формула его вычисления выглядит следующим образом: p = ( a + b + c) / 2. Этот тип задачи несколько проще, чем предыдущий, поэтому больше не нужно никаких промежуточных расчетов.

Радиус вписанной окружности вычисляется по следующей формуле: R = √((p — a) * (p — b) * (p — c) / p). Рассмотрим это на конкретном примере. Предположим, в задаче описан треугольник со сторонами 5, 7 и 10 см. В него вписана окружность, радиус которой и нужно найти. Сначала находим полупериметр. В нашей задаче он будет равен 11 см. Теперь подставляем его в основную формулу. Радиус окажется равным 1,65 сантиметрам. Записываем ответ и не забываем о правильных единицах измерения.

Видео:СЕРЬЁЗНО готовимся к ОГЭ 2024! / Полный прогон задания 17 на ОГЭ по математикеСкачать

Окружность и ее свойства

У каждой геометрической фигуры есть свои особенности. Именно от их понимания зависит правильность решения задач. Есть они и у окружности. Зачастую их используют при решении примеров с описанными или вписанными фигурами, поскольку они дают ясное представление о такой ситуации. Среди них:

• Прямая может иметь ноль, одну или две точки пересечения с окружностью. В первом случае она с ней не пересекается, во втором является касательной, в третьем – секущей.
• Если взять три точки, что не лежат на одной прямой, то через них можно привести только одну окружность.
• Прямая может быть касательной сразу двух фигур. В этом случае она будет проходить через точку, которая лежит на отрезке, соединяющем центры окружностей. Его длина равна сумме радиусов данных фигур.
• Через одну или две точки можно провести бесконечное количество окружностей.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

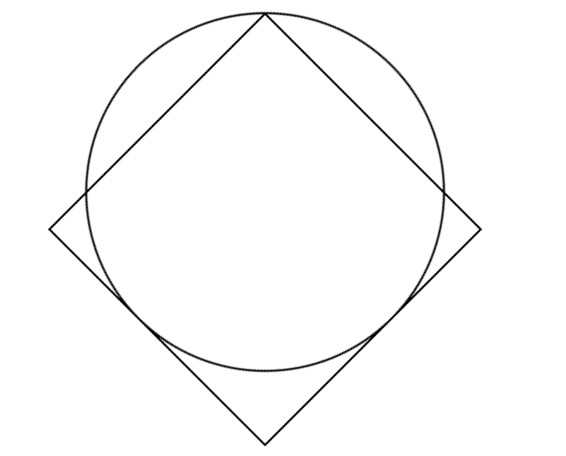
Найти радиус вписанной окружности квадрата c известным радиусом описанной окружности онлайн с формулами расчётов

Введите в поле «радиус описанной окружности» Ваше измерение и нажмите «Рассчитать»

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Округление:

Радиус описанной окружности (R2) = 10

Диагональ, диаметр описанной окружности (M) = (R2*2) = (10*2) = 20

Cторона, диаметр вписанной окружности (L) = (sqrt<frac<M^>>) = (sqrt<frac<20^>>) = 14.14

Радиус вписанной окружности (R1) = (frac) = (frac) = 7.07

Периметр (P) = (L*4) = (14.14*4) = 56.56

📽️ Видео

найти радиус окружности, описанной вокруг треугольникаСкачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Сможешь найти радиус вписанной окружности?Скачать

Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Радиус вписанной окружности #математика #егэ #математикапрофиль2023 #fyp #школаСкачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать