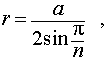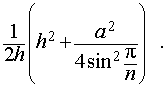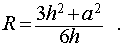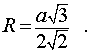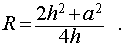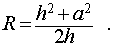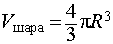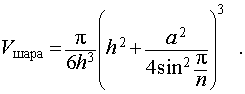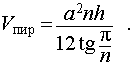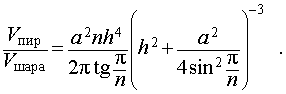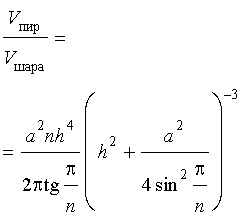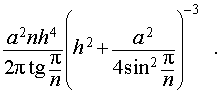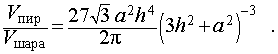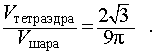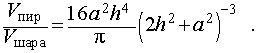Как найти радиус описанной окружности около основания правильной пирамиды

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

Видео:Вычисление радиуса сферы, описанной около правильной треугольной пирамидыСкачать

Формулы расчета радиуса сферы (шара)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

• a – ребро основания пирамиды;
• h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

Видео:Радиус описанной окружностиСкачать

Как найти радиус окружности описанной около пирамиды

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Нахождение радиуса сферы (шара), описанной около правильной пирамиды

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

Видео:Как достроить равногранный тетраэдр и найти радиус описанной сферыСкачать

Формулы расчета радиуса сферы (шара)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

• a – ребро основания пирамиды;
• h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Пирамида, вписанная в сферу

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

Радиус сферы, описанной около правильной n — угольной пирамиды

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Видео:Нахождение радиуса сферы, описанной около пирамидыСкачать

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

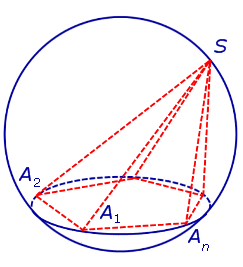
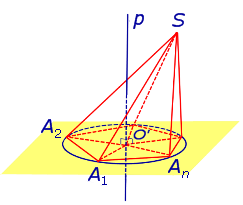
Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.

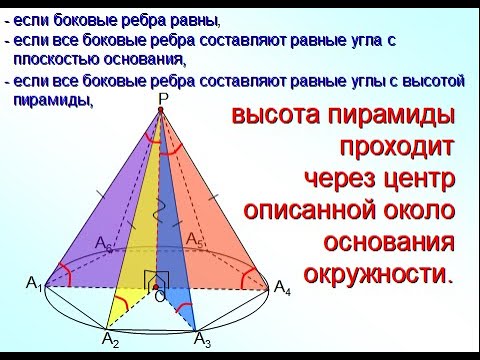
Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

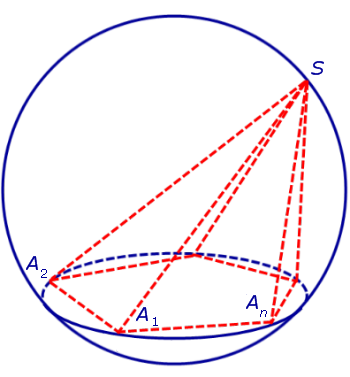
На рисунке 2 изображена пирамида SA₁A₂ . A_n , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A₁A₂ . A_n – основание пирамиды. Доказано.

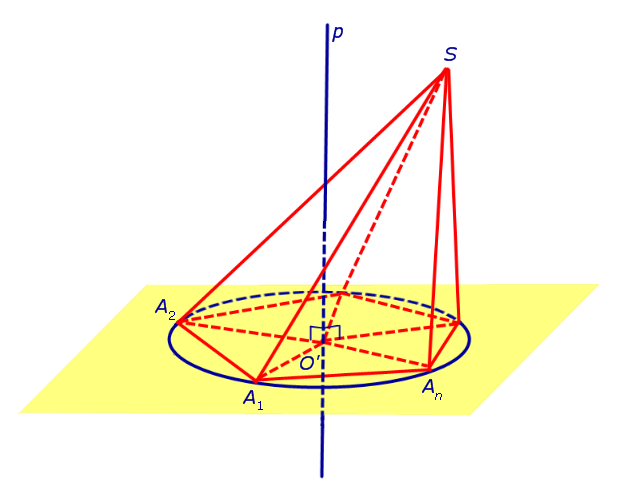
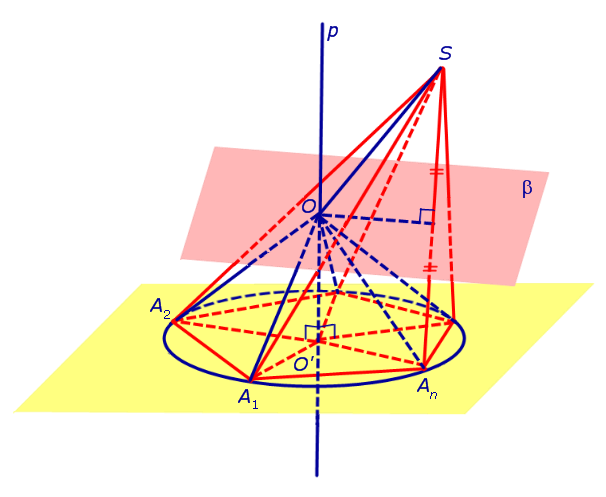
Теперь предположим, что около основания A₁A₂ . A_n пирамиды SA₁A₂ . A_n можно описать окружность. Докажем, что в этом случае около пирамиды SA₁A₂ . A_n можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A₁A₂ . A_n , символом O’ и проведем прямую p, проходящую через точку O’ и перпендикулярную к плоскости многоугольника A₁A₂ . A_n (рис. 3).

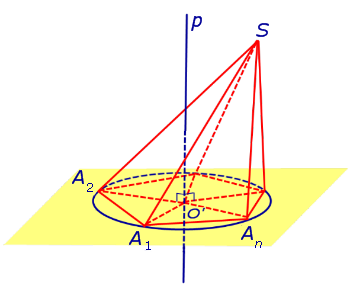
Рассмотрим плоскость β, проходящую через середину отрезка SA_n и перпендикулярную к этому отрезку. Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA₁A₂ . A_n . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.

Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA₁A₂ . A_n . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA₁A₂ . A_n .

Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A₁A₂ . A_n , что противоречит определению пирамиды.

Следствие 1. Около любой правильной пирамиды можно описать сферу.

Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.

Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Радиус сферы, описанной около правильной n — угольной пирамиды

Задача 1. Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.

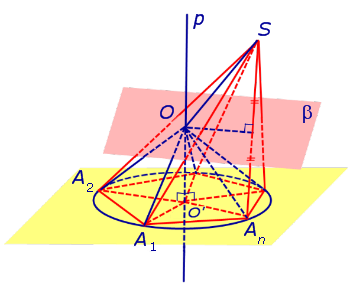
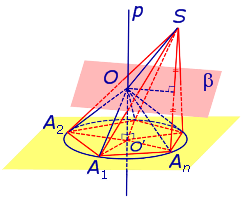
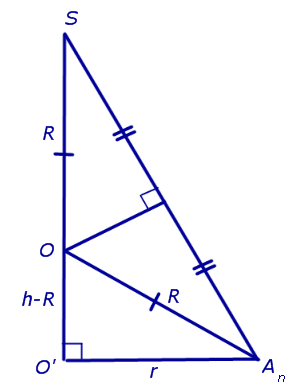
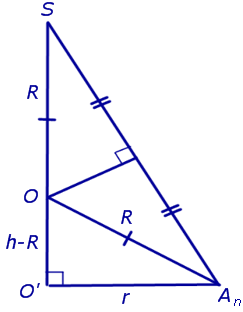
Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’A_n (рис. 5).

Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OA_n получаем

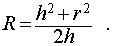(1)

из формулы (1) получаем соотношение

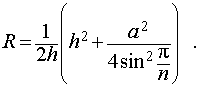(2)

Ответ.

Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен

Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен

Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен

Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен

Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Задача 2. Около правильной n — угольной пирамиды с высотой h и ребром основания a описана сфера. Найти отношение объемов пирамиды и шара, ограниченного сферой, описанной около данной пирамиды.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около пирамиды сферой, через высоту и ребро основания пирамиды:

Ответ.

Следствие 7. Отношение объема правильной треугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной пирамиды, равно

Следствие 8. Отношение объема правильного тетраэдр с ребром a к объему шара, ограниченного сферой, описанной около данного тетраэдра, равно

Следствие 9. Отношение объема правильной четырехугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 10. Отношение объема правильной шестиугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Видео:Окружность вписана в равносторонний треугольник, найти радиусСкачать

Радиус окружности описанной около основания правильной

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Нахождение радиуса сферы (шара), описанной около правильной пирамиды

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Формулы расчета радиуса сферы (шара)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

• a – ребро основания пирамиды;
• h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

Видео:Археологи - Уникальные открытия: что мы знаем о пирамидах?Скачать

Пирамида, вписанная в сферу

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

Радиус сферы, описанной около правильной n — угольной пирамиды

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Видео:🔴 Стороны основания правильной шестиугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.

Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

На рисунке 2 изображена пирамида SA₁A₂ . A_n , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A₁A₂ . A_n – основание пирамиды. Доказано.

Теперь предположим, что около основания A₁A₂ . A_n пирамиды SA₁A₂ . A_n можно описать окружность. Докажем, что в этом случае около пирамиды SA₁A₂ . A_n можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A₁A₂ . A_n , символом O’ и проведем прямую p, проходящую через точку O’ и перпендикулярную к плоскости многоугольника A₁A₂ . A_n (рис. 3).

Рассмотрим плоскость β, проходящую через середину отрезка SA_n и перпендикулярную к этому отрезку. Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA₁A₂ . A_n . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.

Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA₁A₂ . A_n . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA₁A₂ . A_n .

Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A₁A₂ . A_n , что противоречит определению пирамиды.

Следствие 1. Около любой правильной пирамиды можно описать сферу.

Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.

Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.

Видео:Быстро находим радиус описанной сферыСкачать

Радиус сферы, описанной около правильной n — угольной пирамиды

Задача 1. Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.

Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’A_n (рис. 5).

Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OA_n получаем

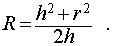(1)

из формулы (1) получаем соотношение

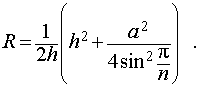(2)

Ответ.

Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен

Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен

Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен

Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен

Видео:№254. В правильной Треугольной пирамиде сторона основания равна а, высота равна Н. НайдитеСкачать

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Задача 2. Около правильной n — угольной пирамиды с высотой h и ребром основания a описана сфера. Найти отношение объемов пирамиды и шара, ограниченного сферой, описанной около данной пирамиды.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около пирамиды сферой, через высоту и ребро основания пирамиды:

Ответ.

Следствие 7. Отношение объема правильной треугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной пирамиды, равно

Следствие 8. Отношение объема правильного тетраэдр с ребром a к объему шара, ограниченного сферой, описанной около данного тетраэдра, равно

Следствие 9. Отношение объема правильной четырехугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 10. Отношение объема правильной шестиугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Видео:Найти радиус описанной сферы около пирамиды Д213Скачать

Радиус окружности описанной около основания правильной

Вопрос по геометрии:

радиус окружности, описанной около основания правильной треугольной пирамиды равен 3. Боковое ребро равно 5. Найдите высоту пирамиды.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Полиночка, все на чертеже. Так строится правильная треуголоная пирамида и только так. AO это радиус описанной окружности.SO находим по т.Пифагора SO^2=5^2=3^2=16, SO=4

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы и свойства правильной четырехугольной пирамиды

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Что собой представляет пирамида

Под пирамидой понимают геометрическую фигуру пространственную, которая получается в результате соединения всех углов многоугольника с одной точкой пространства. Рисунок ниже демонстрирует расположение линий (ребер) для четырехугольной и пятиугольной пирамид.

Многоугольная грань фигуры называется ее основанием. Точка, где все треугольные грани соединяются, называется вершиной. Для определения высоты пирамиды отмеченные элементы являются важными.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Правильная треугольная пирамида.

Правильная треугольная пирамида – это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Элементы правильной пирамиды

• Высота боковой грани, проведенная из ее вершины называется апофема. На рисунке обозначена как отрезок ON
• Точка, соединяющая боковые рёбра и не лежащая в плоскости основания, называется вершиной пирамиды (О)
• Треугольники, имеющие общую сторону с основанием и одну из вершин, совпадающую с вершиной, называются боковыми гранями (AOD, DOC, COB, AOB)
• Отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания называется высотой пирамиды (ОК)
• Диагональное сечение пирамиды – это сечение, проходящее через вершину и диагональ основания (AOC, BOD)
• Многоугольник, которому не принадлежит вершина пирамиды, называется основанием пирамиды (ABCD)

Если в основании правильной пирамиды лежит треугольник, четырехугольник и т.д. то она называется правильной треугольной , четырехугольной и т.д.

Треугольная пирамида есть четырехгранник — тетраэдр .

Высота фигуры

Высотой пирамиды называется перпендикуляр, который из ее вершины опущен на плоскость основания. Важно понимать, что из каждой вершины, принадлежащей основанию фигуры, тоже можно провести перпендикуляр к соответствующей треугольной грани, однако он высотой не будет являться. Высота пирамиды – это единственный перпендикуляр, который является одной из важных ее линейных характеристик.

Каждому школьнику известно, что любая плоская фигура обладает геометрическим центром (в физике ему соответствует центр масс). Например, геометрический центр для произвольного треугольника определяется точкой пересечения его медиан, для параллелограмма – точкой пересечения диагоналей. Если высота пирамиды пересекает ее основание в геометрическом центре, то фигура называется прямой. Пирамида прямая, имеющая в основании многоугольник с одинаковыми сторонами и углами, называется правильной.

Рисунок выше показывает, чем отличается неправильная пирамида от правильной. Видно, что высота неправильной фигуры лежит за пределами ее основания, в то время как у правильной шестиугольной пирамиды высота находится внутри фигуры, пересекая ее основание в центре геометрическом.

Важными свойствами всех правильных пирамид являются следующие:

• все боковые грани представляют собой равнобедренные треугольники и равны друг другу;
• длины боковых ребер и апофем являются одинаковыми.

Что такое пирамида в общем случае?

В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Мы видим что первая фигура имеет треугольное основание, вторая – четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

• в основании должен находиться правильный многоугольник;
• боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Объем пирамиды

Формула для нахождения объема пирамиды через площадь основания и высоту:

<V= dfrac S h> , где S — площадь основания, h — высота пирамиды.

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр

Верно и обратное.

Правильная пирамида с треугольным основанием

Фигура, которая получена с использованием произвольного треугольника и точки в пространстве, будет неправильной наклонной пирамидой в общем случае. Теперь представим, что исходный треугольник имеет одинаковые стороны, а точка пространства расположена точно над его геометрическим центром на расстоянии h от плоскости треугольника. Построенная с использованием этих исходных данных пирамида будет правильной.

Очевидно, что число ребер, сторон и вершин у правильной треугольной пирамиды будет таким же, как у пирамиды, построенной из произвольного треугольника.

Однако правильная фигура обладает некоторыми отличительными чертами:

• ее высота, проведенная из вершины, точно пересечет основание в геометрическом центре (точка пересечения медиан);
• боковая поверхность такой пирамиды образована тремя одинаковыми треугольниками, которые являются равнобедренными или равносторонними.

Правильная треугольная пирамида является не только чисто теоретическим геометрическим объектом. Некоторые структуры в природе имеют ее форму, например кристаллическая решетка алмаза, где атом углерода соединен с четырьмя такими же атомами ковалентными связями, или молекула метана, где вершины пирамиды образованы атомами водорода.

Формулы для высоты правильной пирамиды

Существует четыре основных линейных характеристики для любой пирамиды правильной:

• сторона основания;
• боковое ребро;
• апофема боковой грани;
• высота фигуры.

Все они связаны математически друг с другом. Обозначим длину стороны основания символом a, высоту — h, апофему — hb и ребро — b. Формулы, которые эти величины связывают, имеют индивидуальный вид для соответствующей n-угольной пирамиды. Например, для правильной пирамиды четырехугольной высоту можно определить по формулам:

Эти формулы следуют из теоремы Пифагора при рассмотрении соответствующих прямоугольных треугольников внутри пирамиды.

Если рассматривается фигура с треугольным основанием, тогда справедливы следующие формулы для высоты правильной пирамиды: