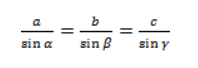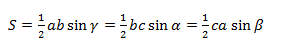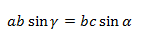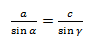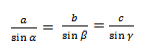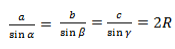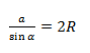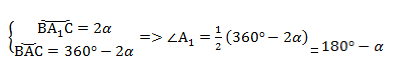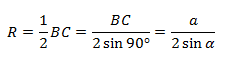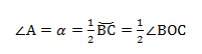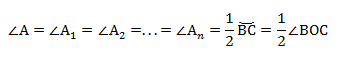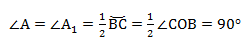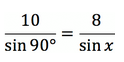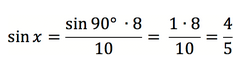Найти радиус описанной окружности через радиус вписанной окружности

Введите в поле «радиус вписанной окружности» Ваше измерение и нажмите «Рассчитать»

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Округление:

Радиус вписанной окружности (R1) = 10

Cторона, диаметр вписанной окружности (L) = (R1*2) = (10*2) = 28.28

Диагональ, диаметр описанной окружности (M) = (2*L^) = (2*20^) = 20

Радиус описанной окружности (R2) = (frac) = (frac) = 14.14

Периметр (P) = (L*4) = (20*4) = 80

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

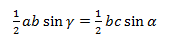
На b сокращаем, синусы переносим в знаменатели:

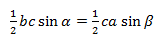
bc sinα = ca sinβ

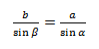
Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

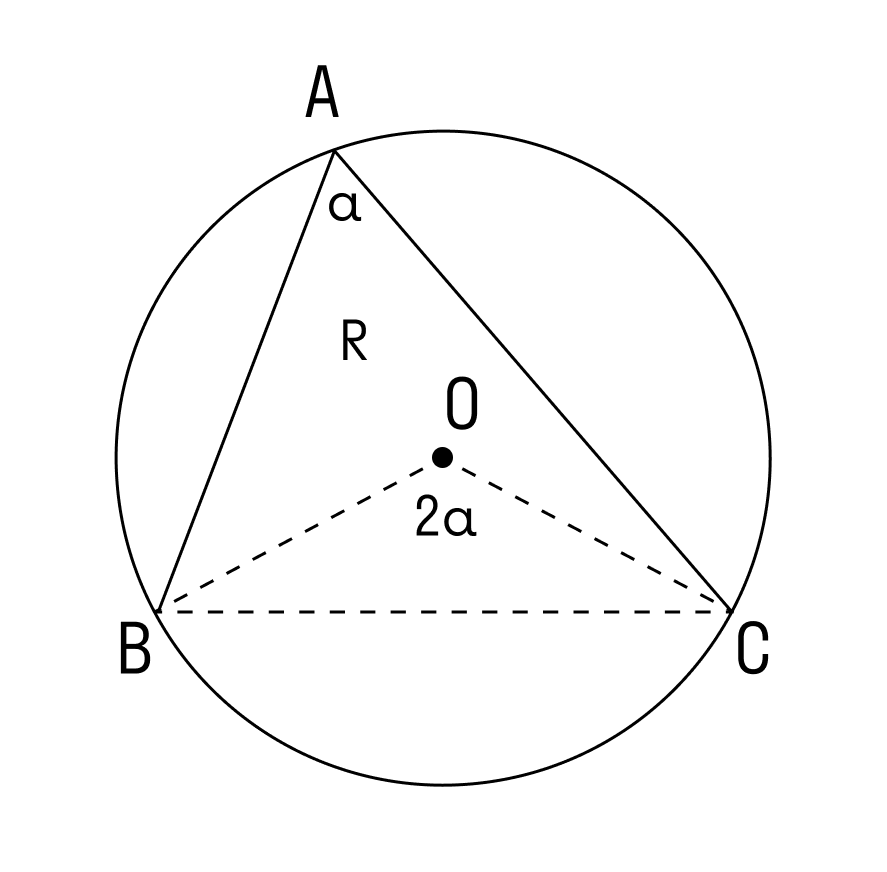
Для доказательства следствия теоремы синусов рассмотрим три случая.

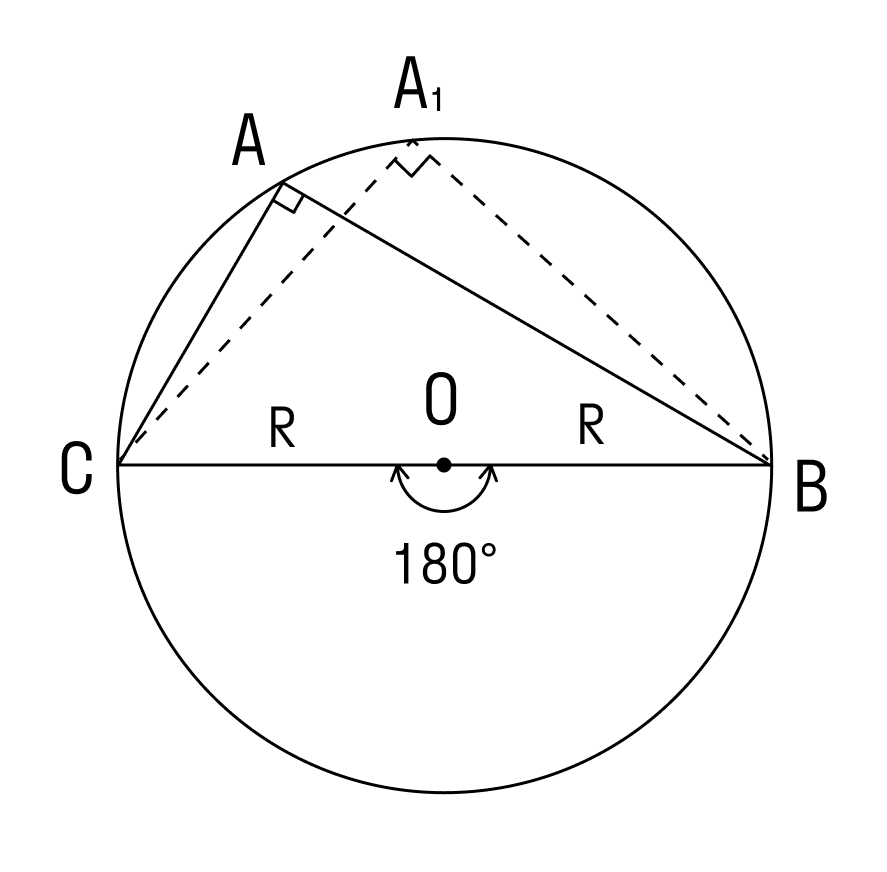
1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° — 60°) = sin60° = 3/√2;
• sin150° = sin(180° — 30°) = sin30° = 1/2;
• sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Видео:Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

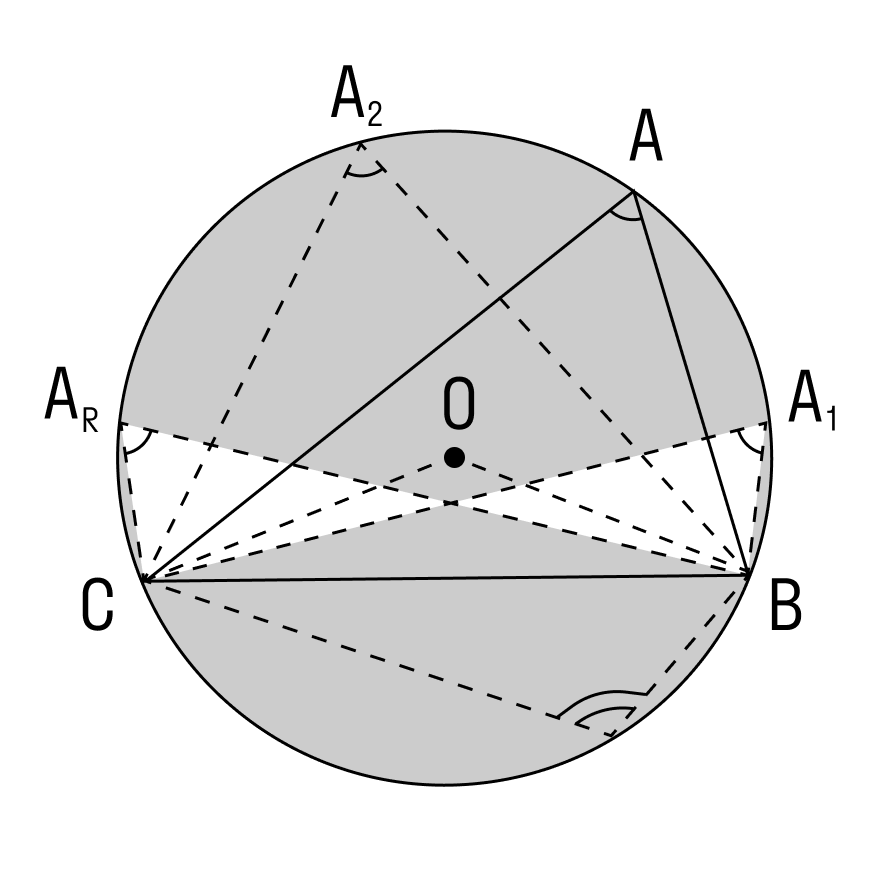
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

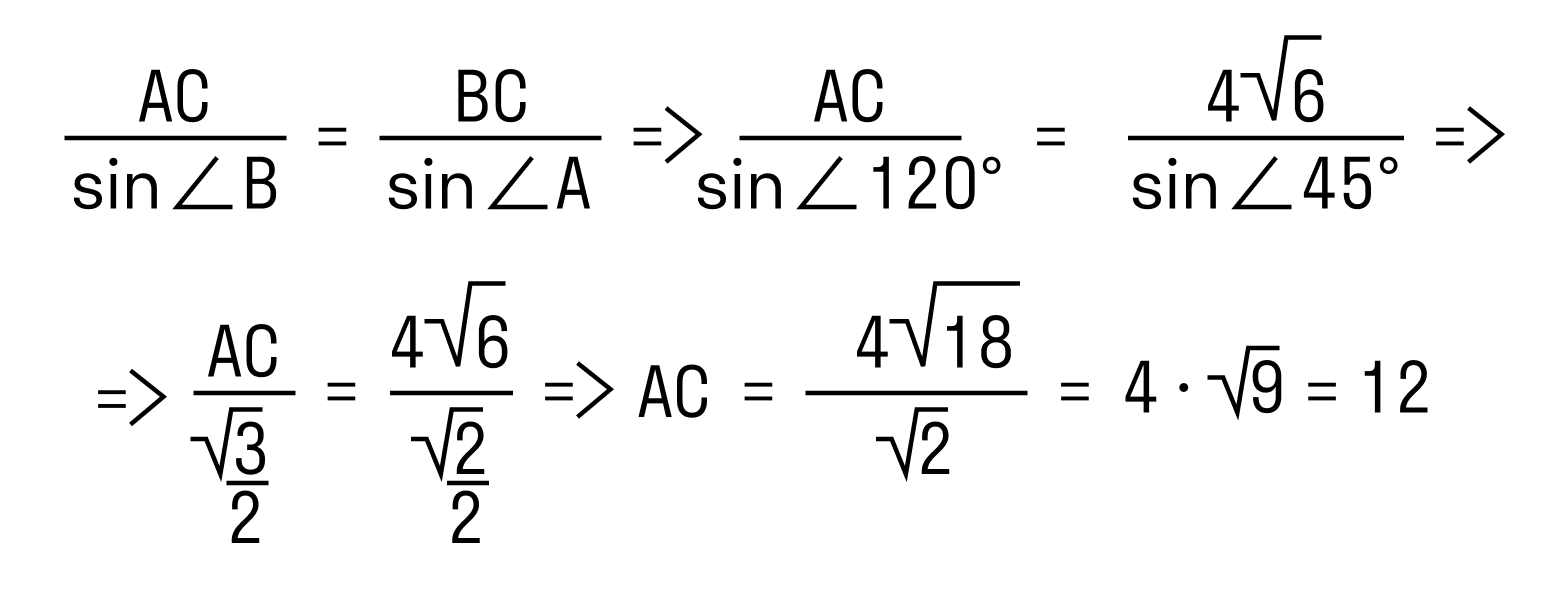
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Видео:ПЛОЩАДЬ КОЛЬЦА. Сделай выбор: на чьей ты стороне?Скачать

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:#233. Теоремы синусов и косинусов | Формулы радиусов окружностейСкачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:Радиус описанной окружности трапецииСкачать

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

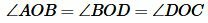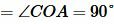(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

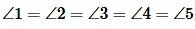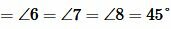(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

📽️ Видео

Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать