Найти площадь прямоугольника вписанного в окружность радиуса (6 видео)

В окружность радиусом 13 см вписан прямоугольник, одна из сторон которого равна 10 см. Найдите площадь прямоугольника.

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
Задача 36461 найти площадь прямоугольника,вписанного.
Условие
Решение
Журнал Педагог
📹 Видео

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Ваш ответ

Видео:2089 Найдите диагональ прямоугольника вписанного в окружность радиус которой равен 5Скачать

решение вопроса

Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

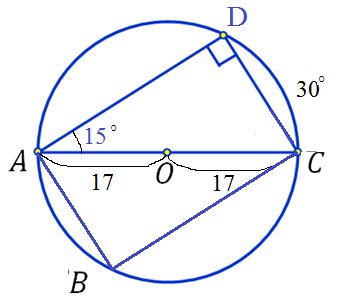
Задача 36461 найти площадь прямоугольника,вписанного.

Условие

найти площадь прямоугольника,вписанного в окружность радиуса 17,если одна из его сторон стягивает дугу 30 градусов.

Решение

Если прямоугольник вписан в окружность, его диагональ является диаметром.
АС= d=2R=34

Диагональ прямоугольника разбивает его на два прямоугольных треугольника АВС и ACD

Пусть ∪ DC=30 градусов.
Вписанный угол измеряется половиной дуги, на которую он опирается. Значит∠ DAC= 15 градусов.

СD=AC*sin∠ DAC=34*sin15^(o)
AD=AC*cos∠ DAC=34*cos15^(o)

=17*34*sin30^(o)=17*34*(1/2)=17*17 [b]=289 [/b]

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Журнал Педагог

Автор: Беспалова Любовь Иннокентьевна
Должность: учитель математики
Учебное заведение: МОУ «Ульканская общеобразовательная школа №2»
Населённый пункт: п.Улькан
Наименование материала: методическая разработка
Тема: Площадь прямоугольника, вписанного в окружность
Раздел: среднее образование

Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №2»
Автор: Беспалова Любовь Иннокентьевна

Тема методической разработки: «Площадь прямоугольника,

вписанного в окружность»,интегрированный урок геометрии

и информатики
2013 П.УЛЬКАН

Тема урока
: Площадь прямоугольника, вписанного в окружность.
Цели урока
:  расширить знания учащихся по теме «Площадь прямоугольника»;  закрепить умения учащихся работать в текстовом редакторе MS Word
Задачи урока
:  Образовательные: вывести формулу площади прямоугольника, вписанного в окружность, через радиус окружности и угол между диагональю прямоугольника и одной из его сторон и исследовать ее; Используя информационные технологии закрепить теоретические знания, полученные на уроках информатики по теме: «Текстовый редактор MS Word» при выполнении исследований;  Развивающие: развитие логического мышления учащихся, навыков набора текста и работы с несколькими документами одновременно;  Воспитательные: воспитание чувства коллективизма, взаимопомощи, взаимоуважения. Точности, аккуратности и внимания в процессе выполнения работы;  Содействовать рациональной организации труда школьников.
Оборудование урока
: OC Microsoft Windos XP, MS Word, проектор, экран, циркули, линейки, плакат « Ги п от е з а –научное предположение, выдвигаемое для объяснения какого – либо явления и требующее проверки на опыте и теоретического обоснования для того, чтобы стать достоверной научной теорией; вообще – предположение, требующее подтверждения» , карточки для выполнения практической работы и для более подготовленных учащихся, таблица «Площади» Площадь прямоугольника a S = ab b Площадь параллелограмма b h S = ah, S = ab sin a Площадь треугольника b c S = ah, S = ab sin , h а S =
a p = Площадь трапеции h S = b Площадь ромба S = d 1 d 2 Площадь квадрата S = a 2 а Площадь треугольника, вписанного в окружность S = а Площадь треугольника, S = описанного около окружности rr b c а 2 Площадь многоугольника, а 3 описанного около а 1 S = rP

окружности d 1 d 2 dddd d a b R c r r r
O

а 4
Тип урока: урок изучения нового материала.

Вид урока — интегрированный: математика, информатика

Продолжительность урока 90 минут

информатики:
Ребята! Сегодняшний урок необычный: урок информатики мы сегодня проводим совместно с геометрией. П.Л. Чебышев сказал: «Сближение теории с практикой дает самые благотворные результаты, и не одна практика от этого выигрывает, сами науки развиваются под ее влиянием». (Слайд 1)
Учитель математики:
Сообщаются тема и цель урока. (Слайд 2)
II.

Проверка домашнего задания:
1.
Учитель математики
: проверим решение задачи 49 из параграфа 14, (Слайд 3) 2.
Учитель информатики:
На компьютерах изобразите решение домашней задачи и отправьте файл, имя которому ваша фамилия на сервер. Учащиеся работают на компьютерах, на экране правильное решение задачи. Подводятся итоги, учитель математики отвечает на вопросы учащихся. (Слайд 4) a 1 Разделим многоугольник на n треугольников с вершинами в rr a 3 центре окружности. S – площадь многоугольника, равна сумме a 2 площадей треугольников (обозначим их S 1, S 2,………., S n ). S = ah, h = r S = S 1 + S 2 + S 3 +……… + S n = a n a 1 r + a 2 r + a 3 r +……..+ a n r = r(a 1 + a 2 +….+ a n ) = rP

a 4

где Р – периметр многоугольника, r – радиус вписанной окружности

Учитель математики:
Фронтальный опрос: а) На доске начерчен прямоугольный треугольник, обозначены его катеты и гипотенуза. Сформулировать и записать теорему Пифагора. б) Дать определение синуса угла в прямоугольном треугольнике. Записать его на доске. r r
O

в) Дать определение косинуса угла в прямоугольном треугольнике. Записать его на доске. г) Записать формулу площади прямоугольника. д) Записать формулу синуса двойного угла. е) Назовите наибольшее и наименьшее значение синуса угла. ж) Где находится точка пересечения диагоналей прямоугольника, вписанного в окружность?
III Изучение нового материала:
1.
Учитель

математики:
Мы с вами научились находить площади прямоугольника, параллелограмма, треугольников, применяя различные формулы, трапеции, ромба, квадрата, треугольников, вписанных в окружность, и треугольников, описанных около окружности, доказали, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус вписанной окружности. (Обратить внимание учащихся на таблицу «Площади») 2. А сегодня на уроке мы попробуем с помощью микроисследования открыть и доказать еще одну формулу для нахождения площади прямоугольника. Учащиеся записывают тему урока: «Площадь прямоугольника, вписанного в окружность». Для этого требуется решить задачу: (слайд 5) Чтобы облегчить решение задачи, давайте мы с вами выполним практическую работу. Только радиус круга возьмем не 50 см, а 5 см. (Обратить внимание учащихся на плакат с разъяснением слова «Гипотеза», на местоположение точки пересечения диагоналей прямоугольника, вписанного в окружность) 3. Практическая работа.
Учитель информатики:
работу выполнить на компьютерах: (каждому ученику дается карточка) Выполни практическую работу. 1. В окружность радиуса 5 см впишите прямоугольник с основанием a см. Величина a принимает значения, указанные в таблице. Заполни таблицу. 2. Назовите наибольшее значение из получившихся площадей. 3. Сформулируйте гипотезу о форме прямоугольника наибольшей площади, вписанного в окружность. 4. Задание для более подготовленных учащихся: a (см) 2 3 4 5 6 7 8 9 b (см) S(см 2 )
Выразить площадь прямоугольника через радиус описанной окружности и угол между стороной прямоугольника и его диагональю. Исследовав эту формулу, ответьте на вопросы: 1. В каком случае площадь прямоугольника будет наибольшей? 2. Какую форму имеет прямоугольник наибольшей площади, вписанный в окружность? 3. Записать формулу площади прямоугольника, имеющего наибольшую площадь. После выполнения практической работы один из учеников выводит результаты исследований на экран в виде таблицы и подтверждает правильность выдвинутой гипотезы. (Ответ учащихся: гипотеза — из всех прямоугольников, вписанных в окружность, наибольшую площадь имеет квадрат).
Учитель математики:
Требуется привести доказательство гипотезы — их всех прямоугольников, вписанных в окружность, наибольшую площадь имеет квадрат. Это делает один из учеников, который выполнял индивидуальную работу. Предполагаемый ответ ученика: Чтобы это доказать, выводим формулу площади прямоугольника, вписанного в окружность через радиус окружности и угол между диагональю прямоугольника и его стороной. A B Центр окружности лежит в точке пересечения диагоналей прямоугольника. АС = 2R. S ABCD = ab. Из прямоугольного треугольника ADC следует, что = , a = 2R , = , b = 2R , S ABCD = ab = 2R 2R = 4R 2 = D C 2R 2 . a (см) 2 3 4 5 6 7 8 9 b (см) S(см 2 ) а b
Площадь прямоугольника, вписанного в окружность, равна 2R 2 , где R –радиус окружности, — угол между диагональю прямоугольника и его стороной. Наш прямоугольник должен по условию задачи иметь наибольшую площадь. Исследуем эту формулу: S = 2R 2 . 2R 2 – величина для этой окружности постоянна. Наибольшее значение площади зависит от , наибольшее значение синуса угла равно 1, тогда = 1, = , = , т.е. угол между диагональю и стороной прямоугольника равен , откуда следует, что прямоугольник наибольшей площади, вписанный в окружность, является квадратом. Тогда площадь квадрата (прямоугольника, имеющего наибольшую площадь) равна S = 2R 2 .
Учитель математики:
1. Получили новые формулы для вычисления площади прямоугольника: S = 2R 2 — площадь прямоугольника, вписанного в окружность, где R – радиус вписанной окружности, — угол между диагональю (диаметром окружности) прямоугольника и стороной прямоугольника. S = 2R 2 – площадь квадрата, вписанного в окружность (прямоугольника, вписанного в окружность наибольшей площади) 2. Задание классу: по полученной формуле найти площадь прямоугольника, имеющего наибольшую площадь, вписанного в окружность. R = 5 см (50 см 2 ) 3. Сравнить значение площади, вычисленной по полученной формуле со значением площади, полученной в результате исследований. 4. Вопрос классу: подтвердилась ли выдвинутая гипотеза: их всех прямоугольников, вписанных в окружность, наибольшую площадь имеет квадрат? 5. Решить задачу: (слайд 5) Из круглого листа жести радиуса 50 см требуется вырезать прямоугольник наибольшей площади. Найти значение этой площади. Учащиеся должны ответить на вопросы: а) Как из круглого листа жести вырезать прямоугольник наибольшей площади? (предполагаемый ответ: на круглом листе жести провести два взаимно перпендикулярных диаметра, концы диаметра последовательно соединить отрезками, получим прямоугольник (квадрат), который имеет наибольшую площадь). (Слайд 6) б) Чему равно значение этой площади? (5000 см 2 )
IV Первичное закрепление материала

1. Решение задач: (выполняется в тетради) — а) Вывести формулу площади квадрата через его диагональ двумя способами. (Слайд 7)

A B 1 способ (Слайд 8) S = a 2 ,

=
45 , a = d sin = d; a S = 2 = 2 , S = 2 .

2 способ (Слайд 9)

C D Квадрат – это ромб, диагонали ромба равны (d 1 = d 2 ).

Формула площади ромба: S = d 1 d 2 , площадь квадрата: S = 2 . б) Боковая сторона равнобедренного треугольника равна 18 см. Найти наибольшую возможную площадь этого треугольника. (Слайд 10) (Слайд 11) A K Треугольник АВС – равнобедренный, АМ – высота, Проведем АК МС, КС АМ, площадь

прямоугольника АКСМ равна площади

треугольника АВС ( АМВ = СКА (равенство

B M C прямоугольных треугольников по двум катетам: АМ = КС, ВМ = МС, МС = АК, тогда АК = МС)). Прямоугольник АКСМ будет иметь наибольшую площадь, если он будет являться квадратом. S кв = 2 , S АКСМ = 18 2 = 324:2 = 162 (см 2 ). Так как площадь прямоугольника АКСМ равна площади треугольника АВС, то наибольшая площадь треугольника АВС равна 162 см 2 .
V Задание на дом:
(Слайд 12) 1. Вывод формулы площади прямоугольника, вписанного в окружность, через диагональ прямоугольника и угол между диагональю прямоугольника и его стороной; 2. Задание по карточке: (карточка выдается каждому учащемуся) d

Домашнее задание
1. Задача: Нужно огородить участок прямоугольной формы забором длиной 200м. Каковы должны быть размеры этого участка, чтобы его площадь была наибольшей? 2. Переформулировать задачу, взяв за периметр прямоугольника 20 см. 3. Заполнить таблицу: a (см) 1 2 3 4 5 6 7 8 9 b (см) S (cм 2 ) 4. Запишите наибольшее значение из получившихся площадей. 5. Сформулируйте гипотезу о форме прямоугольника заданного периметра, имеющего наибольшую площадь. 6. Решить данную задачу. 7. Выполни задание в среде MS Word. 3. (
Учитель математики)
(Слайд 13)
Тест

1.
Площадь ромба с диагоналями 10 см и 20 см равна: а) 200 см 2 б) 300 см 2 в) 400 см 2 г) 100 см 2 2. Площадь квадрата со стороной 5 см равна: а) 20 см 2 б) 10 см 2 в) 25 см 2 г) 15 см 2 3. Боковая сторона равнобедренного треугольника равна 24 см. При каком значении высоты площадь треугольника будет наибольшей? Проверяется результат, анализируется решение задачи. а) 12 см; б) 12 см; в) 12 см; г) 8 см.
VI Итог урока

1.
Вопросы классу: (
Учитель математики)
а) формула площади прямоугольника, вписанного в окружность, через радиус окружности и угол между диагональю прямоугольника и его стороной; какую форму имеет прямоугольник, вписанный в окружность, наибольшей площади? б) формула площади квадрата через его диагональ.
Учитель информатики
: -Какие функции необходимо использовать при вставке фигур в документ? — Какими способами можно задать таблицу в MS WORD? 2. Выставление оценок по математике и информатике.

Учитель математики:
Закончить сегодняшний урок хочется словами великого Леонардо до Винчи: « Железо ржавеет, не находя себе применения, стоячая вода гниет или на холоде замерзает, а ум человека, не находя себе применения, чахнет». Мы хотим, чтобы ваш ум никогда не зачах. (Слайд 14)
Литература
1. Современный словарь иностранных слов. Москва «Русский язык», 1993 г. 2. А.В.Погорелов «Геометрия 7 – 9», учебник, «Просвещение» 2005 г. 3. Т.И.Купорова «Геометрия 9 класс, поурочные планы по учебнику А.В.Погорелова», Волгоград «Учитель», 2003 г. 4. И.М.Шапиро «Использование задач с практическим содержанием в преподавании математики», Москва «Просвещение», 1990 г. 5. А.Г.Мордкович «Алгебра и начала математического анализа 10 – 11, часть 2, задачник», Москва «Просвещение», 2009 г. 6. А.А. Кузнецов, Н.В. Апатова «Основы информатики», «Просвещение», 2008 г 7. А.А.Журин, И.П.Журина «Word 7.0 для школьников» «Дрофа», 2007 г.