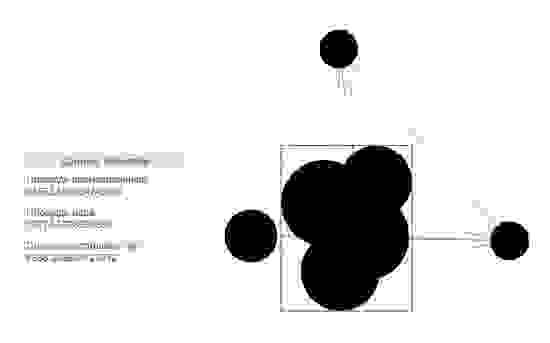
Найти пересечение трех окружностей (5 видео)

Расчет площади пересечения окружностей методом Монте-Карло

Эта статья родилась как логическое продолжение пятничного поста о методе Бутстрапа, а особенно, комментариев к нему. Не защищая метод Бутстрапа, стоит уделить внимание методам Монте-Карло. Здесь я хочу поделиться своим опытом применения Монте-Карло в одной из своих практических задач, а также обоснованием законности этого применения.

Итак, моя задача заключалась в необходимости вычисления площади фигуры, являющейся пересечением окружностей, с последующей реализацией на языке JavaScript. Площадь под графиком – это интеграл. Интегрирование методом Монте-Карло достаточно широко известно, но, как многие верно заметят, его применение требует некоторого обоснования. За подробностями прошу под кат.

Содержание

Обоснование
Реализация задачи на JavaScript
Пара гвоздей в метод Бутстрапа
Как определить пересечение трех кругов?
Пересечение двух окружностей
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Пересечение окружностей
🔍 Видео

Обоснование

Задача расчета площади пересечения двух окружностей является тривиальной геометрической задачей (координаты центров окружностей и их радиусы нам известны). Площадь пересечения двух окружностей – это сумма площадей соответствующих сегментов этих окружностей. Есть решения для расчета площади пересечения двух, трех, четырех окружностей в различных частных случаях.

А вот решения общего случая для пересечения даже трех окружностей уже далеко не так тривиальны. В процессе поиска я нашел даже исследования по расчету площади пересечения N окружностей, однако они настолько же интересны, насколько и сложны.

Здесь на сцену выходит метод Монте-Карло. Благодаря современным компьютерным мощностям этот метод позволяет провести большое количество статистических испытаний, на основе результатов которых делается обобщение.

Итак, алгоритм расчета площади любой фигуры методом Монте-Карло сводится к следующему:

Фигура вписывается в прямоугольник. Координаты сторон прямоугольника известны, значит, известна его площадь.
Псевдослучайным образом внутри прямоугольника генерируется большое количество точек. Для каждой точки определяется, попала ли точка внутрь исходной фигуры или нет.
В результате площадь исходной фигуры вычисляется исходя из обычной пропорции: отношение количества точек, попавших в фигуру, к общему количеству сгенерированных точек равно отношению площади фигуры к площади ограничивающего ее прямоугольника.

Последняя проблема, которую надо решить, заключается в том, что каким-то образом необходимо определять, попала ли точка внутрь исходной фигуры. В моем случае данная задача решается достаточно просто, поскольку моя фигура состоит из окружностей, координаты центров и радиусы которых известны.

Реализация задачи на JavaScript

Пара гвоздей в метод Бутстрапа

Если говорить именно о методе Бутстрапа, то мое личное мнение заключается в том, что случайная генерация набора данных по имеющемуся набору в общем случае не может служить для оценки закономерностей, поскольку сгенерированная информация не является достоверной. В общем, это же, только более умными (и нередко более резкими) словами, говорят и многие авторы, например, Орлов в своем учебнике по Эконометрике.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Как определить пересечение трех кругов?

Учитывая три круга с их центральной точкой и радиусом, как вы можете определить область пересечения?

До сих пор у меня есть:

Кроме того, если два сталкиваются, но не третье, функция должна возвращать значение null.
Если никто не сталкивается, null должен быть возвращен.

В этой статье описывается, как найти область пересечения между двумя кругами. В результате он легко распространяется на три круга.

————- ————- EDIT
Хорошо, проблема нелегко распространиться на три круга, я нашел кандидатские диссертации по этому вопросу. Предполагая, что три круга пересекаются, как показано ниже, можно найти приблизительное решение (я думаю). Прежде чем мы попытаемся это сделать, мы должны проверить, действительно ли три окружности пересекаются, как показано ниже. Проблема изменяется совсем немного, если говорят, что один круг находится внутри другого, а третий пересекает их обоих.

Пусть S1, S2 и S3 обозначают области трех окружностей, а X1, X2 и X3 обозначают площадь пересечений между каждой парой окружностей (индекс увеличивается по часовой стрелке). Как мы уже установили, для них существуют точные формулы. Рассмотрим следующую систему линейных уравнений:

A + D + F + G = A + D + X1 = S1

B + D + E + G = B + D + X3 = S2

B + E + D + G = B + E + X2 = S3

Это недоопределено, но приближенное решение можно найти, используя наименьшие квадраты. Я не пробовал это численно, но вернусь к вам, как только я это сделаю: D
Если решение с наименьшими квадратами кажется неправильным, мы должны также наложить несколько ограничений, например. площадь, если пересечение любой пары кругов меньше площади окружностей.
Комментарии приветствуются.

PS +1 к Саймону для указания, что я не должен квалифицировать вещи так же легко

Видео:Взаимное расположение окружностей. Точки пересечения окружностейСкачать

Пересечение двух окружностей

Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют

Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.

Формулы для расчета приведены под калькулятором.

Точки пересечения двух окружностей

Первая окружность

Вторая окружность

Видео:Алгоритмы. Пересечение окружностейСкачать

Пересечение окружностей

Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.

При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):

Случай	Описание	Условие
Тривиальный случай — окружности совпадают (это одна и та же окружность)
Окружности не касаются друг друга	r1 + r2″ />
Одна окружность содержится внутри другой и не касается ее
Окружности пересекаются в двух точках	Не выполнено ни одно из условий выше
Окружности соприкасаются в одной точке	Частный случай предыдущего

Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:

Сначала калькулятор находит отрезок a

Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):

И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:

Обратите внимание на разные знаки перед вторым слагаемым

По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres