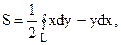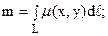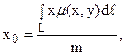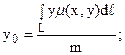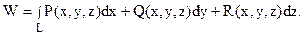Найти массу четверти окружности радиуса

Приложения определенного интеграла к решению некоторых задач механики и физики

1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность 1) <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

002.gif» />=<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

002.gif» />(x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны

<img src="http://ic3.static.km.ru/img/61260

моменты инерции IХ и Iу относительно тех же осей Ох и Оу вычисляются по формулам

<img src="http://ic3.static.km.ru/img/61260

а координаты центра масс <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

009.gif» /> и <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

011.gif» /> — по формулам

<img src="http://ic3.static.km.ru/img/61260

где l— масса дуги, т. е.

<img src="http://ic3.static.km.ru/img/61260

Пример 1. Найти статические моменты и моменты инерции относительно осей Ох

и Оу дуги цепной линии y=chx при 0≤x≤1.

1) Всюду в задачах, где плотность не указана, предполагается, что кривая однородна и <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

◄ Имеем: <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

<img src="http://ic3.static.km.ru/img/61260

Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти.

◄ Имеем: <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

В приложениях часто оказывается полезной следующая

Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.

Пример 3. Найти координаты центра масс полуокружности <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

◄Вследствие симметрии <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

026.gif» />. При вращении полуокружности вокруг оси Ох получается сфера, площадь поверхности которой равна <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

028.gif» />, а длина полуокружности равна па. По теореме Гульдена имеем <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

Отсюда <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

032.gif» />, т.е. центр масс C имеет координаты C<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах 4—7.

Пример 4. Скорость прямолинейного движения тела выражается формулой <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

036.gif» /> (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

◄ Так как путь, пройденный телом со скоростью <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61260

038.gif» />(t) за отрезок времени [t1,t2], выражается интегралом

<img src="http://ic3.static.km.ru/img/61260

Пример 5. Какую работу необходимо затратить для того, чтобы тело массы m поднять с поверхности Земли, радиус которой R, на высоту /i? Чему равна работа, если тело удаляется в бесконечность?

Найти массу четверти окружности радиуса

1. Вычисление объема тела

Пусть функция f ( x ; y ) ≥ 0. Рассмотрим тело, ограниченное поверхностью z = f ( x ; y ), плоскостью z = 0 и цилиндрической поверхностью, образующие которой параллельны оси 0 z , а направляющей служит граница области D . Как было показано выше, согласно формуле (6.3) объем данного тела равен

Пример 6.9. Вычислить объём тела, ограниченного параболоидом z = x 2 + y 2 + 1, плоскостью x + y –3=0 и координатными плоскостями.

Решение. Основанием тела служит треугольник ОАВ. Область D в данном случае определяется неравенствами:

2. Вычисление площади плоской фигуры

Если положить в формуле (6.18) f ( x , y )=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h = 1. Объем такого цилиндра,

как известно, численно равен площади S основания D . Получаем формулу для вычисления площади S области D :

или, в полярных координатах,

Пример 6.10. Вычислить площадь фигуры, ограниченной прямой y = 2 x + 1 и параболой y = x 2 + 1.

Решение. Решая совместно систему

Применяя формулу (6.19), будем иметь:

Решение. Переходим к полярной системе координат, полагая x = r cos φ и y = r sin φ ; тогда получаем

3. Вычисление массы плоской фигуры (пластины)

Масса плоской пластинки D с переменной плотностью γ =γ ( x , y ) находится по формуле

4. Определение статических моментов и координат центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей 0 x и 0 y могут быть вычислены по формулам

а координаты центра масс фигуры – по формулам

Статические моменты широко используются в сопротивлении материалов и других технических науках.

5. Определение моментов инерции плоской фигуры

Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т.е. . Моменты инерции плоской фигуры относительно 0 x и 0 y могут быть вычислены по формулам:

Момент инерции фигуры относительно начала координат – по формуле

Пример 6.12 . Найти массу, статические моменты и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями. Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

Решение. По формуле (6.21) находим массу пластины. По условию, γ =γ ( x , y )= k ∙ xy , где k – коэффициент пропорциональности.Тогда

Находим статические моменты пластинки по формулам (6.22):

Находим координаты центра тяжести пластинки, используя формулы (6.23):

6. Поверхностный интеграл I рода

Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве О xyz в точках некоторой поверхности площади S определена непрерывная функция u = f ( x ; y ; z ). Разобьем поверхность на конечное число n частей S_i , площади которых равны ∆ S_i , а диаметры – d_i , . Выберем в каждой части S_i произвольную точку M_i ( x_i ; y_i ; z_i ) и составим сумму произведений вида

Она называется интегральной суммой для функции f ( x ; y ; z ) по поверхности S . Если при интегральная сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек M_i ( x_i ; y_i ; z_i ), то он называется поверхностным интегралом I рода от функции f ( x ; y ; z ) по поверхности S и обозначается . Следовательно,

Теорема 6.3 (о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f ( x ; y ; z ) непрерывна на этой поверхности, то поверхностный интеграл существует

Формула (6.28)

выражает интеграл по поверхности S через двойной интеграл по проекции S на плоскость x 0 y . Отметим, что если поверхность S задана уравнением вида y=y(x;z) или x=x(y;z), то аналогично получим:

где D ₁ и D ₂ – проекции поверхности S на координатные плоскости xО z и y О z соответственно.

Пример 6.13. Вычислить , где S – часть цилиндрической поверхности , отсеченной плоскостями z = 0 и z = 3.

Решение . Из уравнения заданной цилиндрической поверхности выразим и учтём, что при x = 0 в плоскости x О y : . Так как частные производные равны , то согласно формуле (6.30), имеем

6.1. Площадь поверхности

Если поверхность S задана уравнением z = f ( x ; y ), a ее проекция на плоскость x 0 y есть область D , в которой z = f ( x ; y ), z_x ( x ; y ) и z_y ( x ; y ) – непрерывные функции, то ее площадь S вычисляется по формуле:

Пример 6.14. Вычислить площадь части плоскости x + y + z = 4, вырезаемой цилиндром x 2 + y 2 = 4 (рис. 6.10).

Чтобы вычислить этот интеграл, введём полярные координаты. Область D определяется: . Следовательно,

Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы γ =γ ( x ; y ; z ) . Все эти величины определяются одним и тем же способом:

– данную область разбивают на конечное число мелких частей;

– делают для каждой такой части предположения, упрощающие задачу;

– находят приближенное значение искомой величины;

– переходят к пределу при неограниченном измельчении разбиения области.

Проиллюстрируем описанный способ на примере определения массы материальной поверхности.

6.2. Масса поверхности

Пусть плотность распределения массы материальной поверхности есть γ =γ ( x ; y ; z ) . Для нахождения массы поверхности:

1. Разбиваем поверхность S на n частей S_i , , площадь которых обозначим ∆ S_i .

2. Выберем произвольную точку M_i ( x_i ; y_i ; z_i ) в каждой области S_i . Предполагаем, что в переделах области S_i плотность постоянна и равна её

4. Суммируя m_i по всей области, получаем: .

5. За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей S_i , то есть

6.3. Моменты и центр тяжести поверхности. С татические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:

Пример 6.15. Вычислить координаты центра тяжести однородной поверхности параболоида z = x 2 + y 2 , ограниченной плоскостью z = 1.

Решение. Вершина заданного параболоида совпадает с началом координат. Так как поверхность однородная (постоянная плотность массы), то, основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен на оси 0 z . Тогда x_c = 0, y_c = 0 и по формуле (6.36) аппликата . Пересечем параболоид поверхностью z = 1, спроектируем линию пересечения на плоскость x 0 y – получим окружность x 2 + y 2 =1 в качестве области D . Вычислим элемент поверхности параболоида z = x 2 + y 2 по формуле (6.31), учитывая, что :

Аналогично, переходя к полярным координатам на плоскости x 0 y , получим:

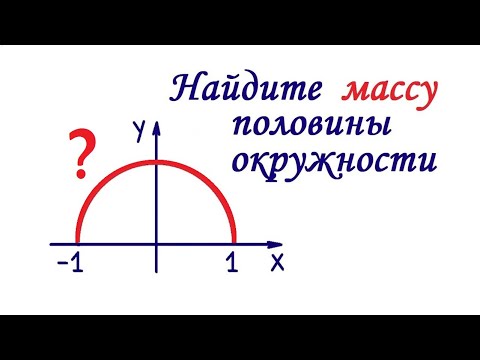
Приложения криволинейных интегралов.

1. Площадь области D, ограниченной замкнутым контуром L, находится по формуле:

( 24)

где направление обхода контура L выбрано так, что область D остается все время слева от пути интегрирования.

2. Пусть L есть плоская кривая с линейной плотностью массы m(x, y),
тогда

а) масса m кривой L вычисляется по формуле

б) координаты центра тяжести кривой L вычисляются по формулам:

( 26)

в) моменты инерции I_x, I_y и I₀ соответственно относительно осей Ox, Oy и начала координат равны:

( 27)

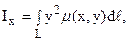
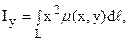
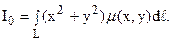
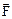
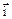
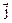
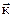
3. Пусть = P(x, y, z) +Q(x, y, z) + R(x, y, z) есть переменная сила, совершающая работу W вдоль пути L, и функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны на кривой L.

( 28)

Найти массу тонкого стержня, имеющего форму линии x 2 + y 2 = 1, y > 0, если его линейная плотность в точке M(x, y) равна m(x, y) = 1 + (1/2)y.

В данном случае линия L есть верхняя половина единичной окружности, которую легко задать параметрически: x = cost, y = sint, 0

Воспользовавшись известными параметрическими уравнениями прямой, запишем уравнения линии, по которой перемещается точка приложения силы:

Þx = 1 + t, y = 1 + 2t, z = 1 + 3t, 0 3 t,
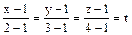
y = asin 3 t, 0