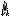1. Произведения отрезков хорд, на которые они длелятся точкой пресечения, равны. То есть (см.рис.1) АО·ОВ=СО·OD.
2. Квадрат касательной равен произведению секущей на её внешнюю часть (см.рис.3): АК²=АМ·АN.
3. Произведения отрезков секущих на их внешнюю часть равны (см.рис.2): ОВ·ОА=ОС·ОD.
Задания для урока:
1. Из точки А, лежащей вне окружности, проведены к ней касательная и секущая. Расстояние от точки А до точки касания равно 16, а от точки А до одной из точек пересечения с окружностью — 32. Найдите радиус окружности, если расстояние от центра окружности до секущей равно5.
2. На окружности радиусом R взяты последовательно точки М, В, Р. так, что угол МВР равен 45º. К- середина отрезка МР. Луч ВК пересекает окружность в точке С, причём КС=3. Найдите ВК.
3. На продолжении диаметра АС окружности отложен отрезок ВС, равный диаметру. Прямая, проходящая через точку С, касается окружности в точке М. Найдите площадь треугольника АСМ, если радиус окружности равен R.
4. Из точки М, расположенной вне окружности на расстоянии √ 7 от центра, проведены касательная МА (А — точка касания) и секущая, внутренная часть которой вдвое меньше внешней и равна R. Найдите R.
5. Из точки А проведены два луча, пересекающие данную окружность: один в точках В и С, а другой — К и Е. Известно, что АВ=7, ВС=7, АК=10. Найдите КЕ.
6. Докажите, что прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
1. Точка М удалена от центра окружности радиуса Rна расстояние d. Прямая, проходящая через точку М, пересекает окружность в точках А и В. Найдите произведение АМ· МВ.
2. В окружности с центром О проведены хорда АВ и СD, пересекающиеся в точке М., причём АМ=4, МВ=1, СМ=2. Найдите угол ОМС.
3. Каждая из боковых сторон АВ ип ВС боковых сторон треугольника АВС разделена на три равные части, и через четыре точки деления на этих сторонах проведена окружность, высекающая на основании АС хорду DЕ. Найдите отношение площадей треугольников АВС и ВDЕ, если АВ=ВС=3 и АС=4.
—>Категория : Мои статьи | —>Добавил : Оптимистка (16.11.2011)
| —>Всего комментариев : 1 | |
Acai Berry — How Come Acai Berry Supplement Great For You? Most because they came from are focused on their bodies know about the health benefits of acai berry products. Acai fruit drink is the similar to acai fruit juice except supply less among the fruit. Acai Capsules are mistakes concentrated capsule or pill that is packed essential vitamins nutrients utilizing the acai berry itself. The Amazonian fruit is a strong defense again health threats that nearly all of us battle with and which usually is why its popularity is growing so extremely fast. Having more energy can produce a powerful impact with a way reside your our life. ORAC (oxygen Radical Absorbance Capacity) score of mangosteen is 167. Содержание
Видео:Как искать точки на тригонометрической окружности.Скачать  Из точки М , расположенной вне окружности, проведены касательные МВ и МА(А и В — точки касания), угол АМВ = 90, АВ = 10 Найдите расстояние от точки М до центра окружности О?Геометрия | 5 — 9 классы Из точки М , расположенной вне окружности, проведены касательные МВ и МА(А и В — точки касания), угол АМВ = 90, АВ = 10 Найдите расстояние от точки М до центра окружности О. Известно, что радиус, проведенный в точку касания, перпендикулярен касательной. Поэтому МВ⊥ВО и МА⊥МО. Тогда четырехугольник МАОВ — прямоугольник с парой смежных равных сторон, т. Диагонали квадрата равны, поэтому АВ = МО = 10. Видео:2017 на окружности по разные стороны от диаметра AB взяты Точки M и NСкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6. Видео:Геометрия Из точки M, находящейся на расстоянии a от окружности, проведена к этой окружностиСкачать  Из точки А вне окружности с центром О проведена касательная В — точка касания найдите длинну окружности если АВ = 10 ОА = 26?Из точки А вне окружности с центром О проведена касательная В — точка касания найдите длинну окружности если АВ = 10 ОА = 26. Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60° , а расстояние от точки А до точки О равно 6. Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Из точки А, лежащей вне окружности с центром в точке О, проведены две касательные?Из точки А, лежащей вне окружности с центром в точке О, проведены две касательные. Найдите угол между ними, если угол между радиусами этой окружности, проведенный в точке касания, равен 120°. Видео:10 класс, 11 урок, Числовая окружностьСкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60° , а расстояние от точки А до точки О равно 6. Видео:Вращательное движение. 10 класс.Скачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60градусов, а радиус окружности равен 10. Видео:Окружность. 7 класс.Скачать  Из точки М к окружности с центром О проведены касательные МА и МВ, А и В — точки касания , Угол АМВ = 70 градусов ?Из точки М к окружности с центром О проведены касательные МА и МВ, А и В — точки касания , Угол АМВ = 70 градусов ! Найдите углы треугольника ОВМ. Видео:№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6. Видео:2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать  ОЧЕНЬ СРОЧНО?Из точки М к окружности с центром О проведены касательные МА и МВ (А и В — точки касания) . Найдите АМ и ВМ если угол АМВ = 90гр. Видео:Точка, прямая и отрезок. 1 часть. 7 класс.Скачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60, а расстояние от точки А до точки О равно 6. Вы открыли страницу вопроса Из точки М , расположенной вне окружности, проведены касательные МВ и МА(А и В — точки касания), угол АМВ = 90, АВ = 10 Найдите расстояние от точки М до центра окружности О?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху. Углы MNH, CNH, CHN — равны по опредеоению биссектрисы и свойству параллельных прямых. Угол С равен 180 — 53 * 2 = 74, АВС — равнобедренный, значит угол А тоже равен 74, а угол В равен 180 — 74 * 2 = 32. Ответ : 74, 74, 32. 1 рассмотрим треугольник kbc и kac. 2 kb = kc ( по условию ) 3 bc = ac ( по условию ) 4 угол kbo = углу kao. ( по условию ). Следовательно углы равны. В прямоугольном треугольнике медиана равна половине гипотенузы. СМ = 12 / 2 = 6 см. Высота СН лежит против угла в 30 градусов и равна 6 / 2 = 3 см. Отрезок МН = 6 * cos 30° = 6 * (√3 / 2) = 3√3 см. Отрезок НА = 6 — 3√3 = 3(2 — √3) см. Сторона АС.. #1 — 73 #2 — 143 #3 угл 3 = 143, угл 2 = 37. 1. задание : найти АС. Что это значит? ЭТО значит, что 6 см + 9 см = 15 см , так как АВ = 6 см , а ВС = 9 см, задание НАЙТИ АС. 2. ЗАДАНИЕ : найти МК всё точно также складываем 12см + 3 см = 15 см 3. Найти ошибку там ты написала правильно что 6, .. Дано : AM = MN = NB и МК||NP||BC. Проведем МЕ и ND параллельно АС. Теорема ФалесаЕсли на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второ.. 24 — 8 = 16см — это ВС АС = 8см. Возможно, кому — то пригодится решение — привожу своё : Пусть BC = AD = aBC = AD = a, тогда из условия BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5. MOMO и ONON найдём как средние линии трапеций .. Решение 22см — одна из сторон, т. К. сумма от точки пересекч к соседним сторонам равна одной стороне. 22 — 6 = 16см — вторая сторона. Х + х — 6 = 22 2х — 6 = 22 2х = 22 + 6 2х = 28 х = 28 / 2 х = 14 одна сторона это Х то есть 14 а вторая х — 6 то есть 14 — 6 = 8. Видео:Теорема ФАЛЕСА. ПОДОБИЕ ТРЕУГОЛЬНИКОВ. Контрольная № 3 Геометрия 8 класс.Часть2Скачать  Примеры решения задач, решаемых методом ГМТЗадача 1. На стороне треугольника найти точку, равноотстоящую от двух других сторон треугольника. Анализ. Пусть задача решена и точка М на стороне АВ находится на одинаковом расстоянии от сторон АС и ВС, образующих угол С. Доказательство. Легко видеть, что точка М удовлетворяет требованиям Задача 2. Построить треугольник по основанию а, углу при вершине А Анализ. Допустим, что задача решена и искомый треугольник ΔАВС построен так, что BC = a, AM = mа – медиана и ∟ВАС = α. 1 0 . Точка А находится на расстоянии mа от середины М стороны ВС, т.е. Таким образом, Доказательство: BC = a, AM = mа по построению, и ∟СВО = 90 0 – α, следовательно, ∟ВОМ = α, следовательно, ∟ВОС=2α, а ∟ВАС =0,5*∟ВОС= α и, следовательно ΔАВС, удовлетворяет всем условиям задачи и потому искомый. Исследование: Задача имеет столько решений, сколько точек содержит пересечение решения; в одной (окружности касаются) – одно решение, не пересекаются –нет решений. Задача 3. Построить окружность данного радиуса r, проходящую через данную точку М и высекающую на данной прямой l отрезок длины d, равный данному. Значит, искомый центр О принадлежит, во-первых ГМТ F1, удаленных от данной прямой l на расстояние, равное ОС(ГМТ 3); во-вторых ГМТ F2, удаленных от данной точки М на расстояние, равное данному радиусу r (гмт2). Для этого построим вспомогательный треугольник О1В1С1 по гипотенузе О1В1 = r и катету В1С1 = d/2. Тогда h = O1C1 будет найден. Действительно, ΔАОВ — равнобедренный (ОС – медиана и высота), отсюда АВ = 2ВС = 2*d/2 = d. Исследование: Построение 1 возможно, если d 0 ) точки О можно отметить сразу – она находится на расстоянии r от стороны ВС, то есть центр О вписанной окружности принадлежит ГМТ, находящихся на расстоянии r от прямой ВС (ГМТ 3). (Как правило, мы строим только в одной из двух полуплоскостей, определяемых заданной прямой). Второе свойство, которым обладает точка О, видно не сразу. Но, исходя из свойств вписанной окружности, это свойство мы можем найти: центр вписанной окружности находится на пересечении биссектрис треугольника и потому ОВ и ОС – биссектрисы углов В и С. Тогда: ∟ВОС = 180 0 – 0,5(∟В + ∟С) = 180 0 – 0,5 (180 0 — ∟А) = 90 0 + 0,5∟А Так как ∟ВОС =90 0 +∟A/2, то точка О принадлежит ГМТ F2, из которых Доказательство: Убеждаемся в том, что построенный треугольник удовлетворяет всем требованиям задачи. ВС = а, окружность ω(O,r) вписана в треугольник по построению. Остается доказать, что ∟ВАС равен данному углу А. Действительно, по построению ∟О1 ВК = ∟А/2. Тогда Теперь находим: Значит, ΔАВС удовлетворяет всем условиям задачи, а потому – искомый. Исследование. Построения 1-3 выполняются и притом однозначно при любых a, r и ∟ A 0 . Построение 4 возможно лишь тогда, когда прямая F1 пересекает окружность F2, то есть при условии двух или одной точке соответственно. Построения 6 и 7 всегда выполнимы, так как из любой точки вне окружности можно провести к ней две касательные (одна из них в данном случае прямая ВС). А вот построение 8 возможно не всегда: прямые m и n могут быть параллельными или могут пересекаться в полуплоскости, не содержащей точку О. В этих случаях в нужной нам полуплоскости точка А не строится. Вывод: при выполнении условий ∟A 0 и (*) задача может иметь одно, два или ни одного решения. 4. Построение Штейнера и построение с помощью Якоб Штейнер (18.05 1795г. – 01.04.1863г.) сын простых поселян из Уцисдорфа Германии. Как он сам писал: «Только на девятнадцатом году стремление к образованию стало для меня потребностью…. и с осени 1822г. Вынужден с величайшим трудом добывать средства к существованию частными уроками. Почти бессознательно я пришел таким образом к собственно геометрическому способу рассмотренья, как оно должно быть присуще геметрии древности, но я находился в случае, противоположном им. Мне было дано множество разрешимых задач и предложений, и мне приходилось заняться не фиксацией отдельных предложений, а установлением того свойства общих законов систематического построения, что из них вытекают все открытия подобного рода, и их соответственным образом исчерпать». «Геометрия в более тесном смысле для своих построений нуждается только в двух инструментах, циркуле и линейке. …. все построения могут быть выполнены только при помощи линейки, если где-либо в дан будет вспомогательный неподвижный круг» Рассмотрим решение задач проведением только одних прямых линий, причём на чертеже иногда уже имеется начерченной какая-нибудь одна вспомогательная фигура. Из всех таких способов наиболее сильными являются решения с помощью: 1. Двусторонней линейки, другие инструменты при этом не допускаются 2. Прямого или острого угла, сделанного из дерева или металла — другие инструменты не допускаются. 3. Односторонней линейки, причём на чертеже уже имеется начерченной окружность с известным центром. Далее, всякая не вспомогательная окружность считается данной, если известно положение ее центра и длина радиуса, заданная где-нибудь начерченным отрезком. Однако ни одна точка такой окружности точку какого-нибудь свойства, то должны ограничиться проведением только прямых линий. Мы знаем, что решение квадратной задачи сводится к известным четырём основным построениям. Из этих основных задач первая и третья решаются способами 1, 2 и 3 непосредственно — одной линейкой. Моя цель показать, что две другие основные задачи решаются теми же тремя способами, которые решают теми же способами всякую квадратную задачу. Решим несколько задач проведением одних прямых линий (односторонней линейкой). Найти геометрическое место центров окружностей, проходящих через две данные точки. Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O — центр окружности, проходящей через точки A и B. Проведем диаметры АА1, ВВ1, затем хорды АВ1, ВА1, эти последние перпендикулярны АВ и потому параллельны между собой. Поэтому для решения задачи нужно провести через точку О прямую, параллельную эти хордам. Она будет серединным перпендикуляром к АВ, т.е. искомым ГМТ [5, стр.21] Дан прямоугольник ABCD. Найдите ГМТ X, для которых AX + BX = CX + DX. Пусть l — прямая, проходящая через середины сторон BC и AD. Предположим, что точка X не лежит на прямой l, например, что точки A и X лежат по одну сторону от прямой l. Тогда AX 📽️ Видео№632. Расстояние от точки А до центра окружности меньше радиуса окружности. Докажите, что любаяСкачать  ОГЭ Задание 16 Окружность, радиус, диаметрСкачать  Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать  Физика - движение по окружностиСкачать  ОГЭ. Метро города N. Задания 1-5.Скачать  №198. Точка А лежит в плоскости α, а точка В удалена от этой плоскости на расстояние 9 см. Точка МСкачать  8. Движения окружности. Алексей Савватеев. 100 уроков математикиСкачать  №573. Точки А и В лежат на сфере с центром O∉АВ, а точка М лежит на отрезке АВ. Докажите, что:Скачать  | |













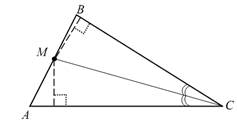
 Так как все точки, равноудаленные от сторон угла С лежат на биссектрисе этого угла (гмт 5), то точка М удовлетворяет двум независимым условиям:
Так как все точки, равноудаленные от сторон угла С лежат на биссектрисе этого угла (гмт 5), то точка М удовлетворяет двум независимым условиям:

 Отрезок ВС, равный данному, всегда может быть построен. Тогда задача сводится к построению точки А, удовлетворяющей двум независимым условиям:
Отрезок ВС, равный данному, всегда может быть построен. Тогда задача сводится к построению точки А, удовлетворяющей двум независимым условиям:
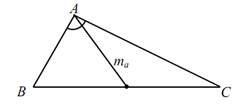
 2 0 . Так как ∟ВАС = α, то точка А принадлежит ГМТ F1, из которых отрезок ВС виден под углом α, т.е.
2 0 . Так как ∟ВАС = α, то точка А принадлежит ГМТ F1, из которых отрезок ВС виден под углом α, т.е.
 Заданные по условию задачи элементы могут быть выбраны перед построением или анализом.
Заданные по условию задачи элементы могут быть выбраны перед построением или анализом.

 двух окружностей. Если пересечение в двух точках, то два
двух окружностей. Если пересечение в двух точках, то два Анализ: Пусть искомая окружность построена. Пусть О – ее центр, r – данный радиус, М – данная точка, АВ – хорда длины d, построенной окружности, лежащей на данной прямой l. Опустим перпендикуляр ОC на прямую l. В прямоугольном треугольнике ОВС известна гипотенуза (данный радиус r) и катет ВС, равный половине данного отрезка. Кроме того, ОМ = r.
Анализ: Пусть искомая окружность построена. Пусть О – ее центр, r – данный радиус, М – данная точка, АВ – хорда длины d, построенной окружности, лежащей на данной прямой l. Опустим перпендикуляр ОC на прямую l. В прямоугольном треугольнике ОВС известна гипотенуза (данный радиус r) и катет ВС, равный половине данного отрезка. Кроме того, ОМ = r. Окружность ω может быть построена, ГМТ F1 может быть построено, если мы найдем расстояние OC = h.
Окружность ω может быть построена, ГМТ F1 может быть построено, если мы найдем расстояние OC = h.
 Построение:
Построение: Доказательство: Убеждаемся в том, что построенная окружность удовлетворяет всем требованиям задачи. OM = r по построению. Докажем, что AB = d.
Доказательство: Убеждаемся в том, что построенная окружность удовлетворяет всем требованиям задачи. OM = r по построению. Докажем, что AB = d. данный отрезок ВС виден под данным углом α = 90 0 + ∟А/2 (ГМТ 6). ГМТ F1 и F2 может быть построено, а потому и точка
данный отрезок ВС виден под данным углом α = 90 0 + ∟А/2 (ГМТ 6). ГМТ F1 и F2 может быть построено, а потому и точка  может быть построена и мы можем перейти к построению искомой фигуры.
может быть построена и мы можем перейти к построению искомой фигуры.


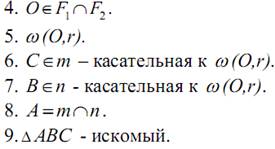


 или при:
или при:  (*). При этом прямая F1 пересекает окружность F2 в
(*). При этом прямая F1 пересекает окружность F2 в