Найти кпд цикла треугольник (2 видео) | Курс школьной геометрии

Найти кпд цикла треугольник

2017-11-06
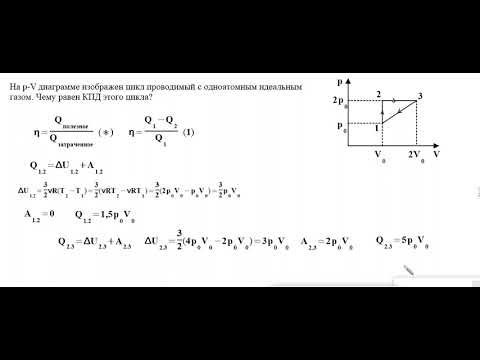
Найдите максимально возможное значение КПД $eta$ цикла, в котором участвует идеальный одноатомный газ. В осях $pV$ цикл имеет форму прямоугольного треугольника, левый катет которого — изохора, а верхний катет — изобара (см. рис.).

Из рис. видно, что

$A = frac Delta p Delta V$. (2)

Тепло, подводимое к газу на изобаре и изохоре, есть

$Q_ = nu c_ Delta T_$, (3)
$Q_

= nu c_

Delta T_$. (4)

$Delta T_$ и $Delta T_$ найдём из уравнения состояния $pV = nu RT$:

$V_ Delta p = nu R Delta T_$,
$p_ Delta V = nu R Delta T_$.

Подставляя (2), (3) и (4) в (1), получим:

Из (5) видно, что при уменьшении $V_$ и $P_$ КПД цикла возрастает. $min V_ = 0, min p_ = Delta P$. Отсюда,

Видео:КПД треугольникСкачать

Найти кпд цикла треугольник

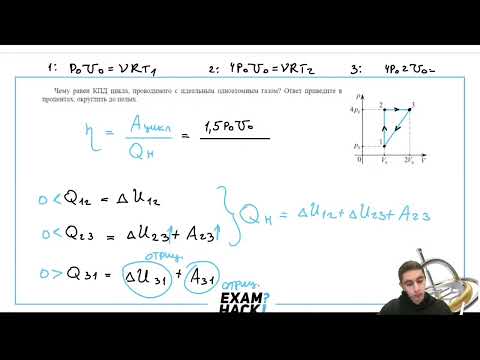
Чему равен КПД цикла, проводимого с идеальным одноатомным газом? Ответ приведите в процентах, округлить до целых.

КПД тепловой машины определяется как отношение полезной работы и переданного рабочему телу тепла за цикл: Определим сперва полезную работу за цикл, на диаграмме этой величине соответствует площадь цикла: Передаваемое газу тепло рассчитаем при помощи первого начала термодинамики: Рассмотрим последовательно все участки цикла. На участке 1 — 2 газ не совершает работы, а изменение его внутренней энергии (с учетом уравнения Клапейрона-Менделеева) равно: Так как изменение внутренней энергии положительно, газ получает тепло на этом участке. На участке 2 — 3 газ совершает работу Изменение его внутренней энергии на этом участке: Следовательно, на этом участке газ получает тепло На участке 3 — 1 газ совершает отрицательную работу, он остывает, а значит, его внутренняя энергия уменьшается, следовательно, на этом участке он отдает тепло, а не получает. Окончательно, все полученное газом за цикл тепло равно Таким образом, КПД цикла равно

А разве здесь не нужно использовать формулу (дельта)U=Q+A, ведь над газом совершают работу, а не газ сам ее совершает. Или как вообще нужно определять в какой задаче какую формулу использовать, разве не нужно ориентироваться по дано задачи?

Формулу можно использовать любую, в зависимости от того, что Вам удобно в данной конкретной задаче. В данной задаче цикл идет по часовой стрелке, следовательно, газ совершает положительную работу, поэтому, возможно, удобнее использовать то, что использовано 🙂

Алексей! Поздравляю Вас. Вы очередной раз «изобрели» вечный двигатель второго рода. Обратите внимание на то, что в условии задачи указано, что газ одноатомный.

Если проделать те же вычисления с двухатомным газом, то значение КПД будет другим, что противоречит первой теореме Карно, которая гласит: «КПД обратимого цикла не зависит от рода вещества, из которого сделано рабочее тело».

Хотелось бы сделать одно замечание по поводу Ваших «тезисов». Один из них гласит: «Квазистатический (протекающий медленно) процесс обратим». Согласно ему, если дизельный двигатель медленно крутить в противоположном направлении, то в топливный бок потечет солярка, а из воздушного фильтра будет выходить очищенный воздух. Ведь, согласно Вашему тезису, все должно возвратиться в исходное положение Неужели Вы поверите этому бреду?!

Мне кажется, этот спор бесконечен. Мой тезис следующий, постараюсь его еще раз передать: «Если на некоторой диаграмме () задана точка, то состояние системы полностью задано и она находится в равновесном состоянии (мы считаем, что уравнение состояния нам известно). Если система не находится в равновесии, то точка на подобных диаграммах вообще не имеет смысла. Далее, когда на диаграмме нарисована линия, это последовательность равновесных состояний, через которые система проходит непрерывно, квазистатически. По линии можно перемещать систему в разных направлениях».

Что касается теоремы Карно, на которую Вы ссылаетесь, мне кажется, что Вы упускаете, существенный факт, что она формулируется для цикла Карно, когда есть нагреватель при одной температуре и холодильник при другой. Для цикла Крно получается все так, как Вы говорите. Но можно придумать огромную кучу оьратимых машин, отличных от машины Карно. Например, можно построить из адиабат и изотерм цикл с тремя температурами. Дальнейшее обобщение дает произвольную кривую. Я Вам уже рассказывал, что любую линию можно построить из адиабат и изотерм. Надеюсь в их обратимости Вы не сомневаетесь.

Ваш пример с двигателем, конечно, не вписывается в эту картину. Процесс превращения топлива в тепло с выбрасыванием продуктов горения нельзя обратить, как ни старайся.

Видео:Физика. 10 класс. Расчёт КПД цикловСкачать

Найти кпд цикла треугольник

1) На каких участках процесса газ получает теплоту, а на каких отдаёт?

2) Чему равно изменение внутренней энергии в конце цикла?

3) Какую работу совершает газ за цикл?

1) Для ответа на первый вопрос задачи необходимо определить знак количества теплоты для каждого участка цикла.

Процесс $$ 1–2$$ – изохорный процесс, идущий с увеличением давления. В этом процессе внутренняя энергия газа увеличивается:

Процесс $$ 2–3$$ изобарный, идущий с увеличением объёма. В этом процессе внутренняя энергия газа увеличивается: $$ Delta _=<displaystyle frac>

_(_-_)>0$$, а работа газа при увеличении объёма положительна: $$ _=

_(_-_)>0$$. Следовательно, на изобаре $$ 2–3$$ газ получает теплоту:

Процесс $$ 3–4$$ – изохорный процесс, идущий с уменьшением давления.

В этом процессе внутренняя энергия газа уменьшается:

`DeltaU_(1-2)=i/2 V_(34)(p_(14)-p_(23)) 0$$ и

на втором процессе – изобарном расширении:

Всего затрачено (а рабочим телом получено)

Т. к. тепло подводится на участках $$ 1–2$$ и $$ 2–3$$ (т. е. на участке $$ 1–2$$), то

2) Работа за цикл находится уже рассмотренным в предыдущем примере

При получении окончательной формулы использовано уравнение состояния идеального газа.

Пусть $$

_=2

_$$, $$ i=3$$, $$ _=3_$$. Тогда для такого случая получаем:

Воздух в комнате объёмом $$ 100 <mathrm>^$$ прогрели от `t_1 = 10^@»C»` до `t_2 = 50^@»C»`. Давление воздуха – нормальное атмосферное. На сколько изменились масса и внутренняя энергия воздуха в комнате при повышении температуры?

Для ответа на первый вопрос воспользуемся уравнением Менделеева – Клапейрона: $$ pV=fracRT$$, откуда $$ m=frac$$. С учётом того, что
процесс расширения воздуха изобарный, то

Минус указывает на убыль массы воздуха в комнате.

Для изменения внутренней энергии запишем: $$ Delta U= <displaystyle frac>(

__-

__)$$. Заметим, что $$

_$$, также $$ _=_=V$$. Эти факты указывают на то, что внутренняя энергия воздуха не изменяется: $$ Delta U=<displaystyle frac>(

__-

__)=0$$.

Из результата можно понять, что убыль внутренней энергии за счёт уменьшения массы равна приросту внутренней энергии за счёт увеличения температуры.

Тогда возникает вопрос целесообразности отопления зданий, ведь внутреннюю энергию при этом мы не увеличиваем. Ответ на вопрос лежит совсем в другой области: увеличение температуры воздуха помогает нашему организму терять меньше энергии (закон Фурье) и тем самым поддерживать скорость химических реакций обмена веществ в организме (метаболизм) на необходимом комфортном уровне.

1) Найти работу, совершённую газом при увеличении его объёма от $$ _$$ до $$ _$$.

2) Поглощается или выделяется энергия в таком процессе?

3) Чему равна молярная теплоёмкость газа в таком процессе?

1) Определим сначала, как давление в этом процессе зависит от объёма при изображении процесса на $$ рV$$-диаграмме. Для этого воспользуемся уравнением Менделеева-Клапейрона: $$ pV=nu RT=nu R·alpha ^$$.

Тогда получим, сокращая объём, что: $$ p=nu R·alpha V=beta ·V$$, где $$ nu R·alpha =beta $$. Видим, что давление изменяется прямо пропорционально объёму, и графиком процесса на $$ pV$$-диаграмме будет отрезок $$ 1–2$$, лежащий на прямой, проходящей через начало координат (см. рис. $$ 23$$).

Работа численно равна площади фигуры под графиком процесса на данной диаграмме. Площадь можно найти геометрически, как площадь трапеции:

2) Так как объём газа увеличивается, и давление тоже растёт, то:

а) Работа газа положительнa $$ ^<text>>0$$.

б) Температура и, как следствие, внутренняя энергия увеличиваются $$ Delta U>0$$.

Следовательно, в этом процессе газ получает теплоту $$ Delta Q= Delta U+^<text>>0$$.

3) Молярная теплоёмкость процесса определяется отношением:

Для одноатомного газа `(i=3)` получаем

В цилиндре под поршнем находится $$ nu =mathrm$$ моль воздуха при температуре $$ _=300$$ K. Во сколько раз увеличится объём газа при сообщении ему количества теплоты $$ Q=mathrm$$ кДж?

Из текста задачи следует, что процесс нагрева газа идёт изобарно (находится в цилиндре под поршнем). Молярная теплоёмкость в таком процессе равна $$ _

=(<displaystyle frac>+1)R=<displaystyle frac>R$$.

Количество теплоты, потраченное (полученное газом) в процессе,

Неизвестное давление $$ р$$ выразим из уравнения Менделеева – Клапейрона: $$ pV= <displaystyle frac>RT$$, откуда $$ p=<displaystyle frac>RT=<displaystyle frac>$$. Подставляя это выражение в предыдущее, получим:

Моль гелия расширяется в изотерми ческом процессе $$ 1–2$$, совершая работу величиной $$ _$$ . Затем газ охлаждается в изобарическом процес се $$ 2–3$$ и, наконец, в адиабатическом процессе $$ 3–1$$ возвращается в исходное состояние (рис. $$ 24$$). Какую работу совершил газ в замкнутом цикле, если раз ность максимальной и минимальной температур газа в нём составила величину $$ Delta Т$$ градусов?

Вспомним, что работа за цикл (замкнутый процесс) равна сумме количеств теплоты, потраченных (переданных газу) в каждом из процессов:

Теперь запишем первый закон термодинамики для каждого процесса в отдельности:

1) В первом процессе температура не изменяется, вся энергия идёт на совершение работы $$ Delta _= Delta _+_=0+_=_$$.

2) На втором процессе температура падает от $$ _$$ до $$ _$$, и данная величина составляет заданную в условии задачи разность температур $$ Delta Т$$ (т. к. $$ _$$ — минимальная температура, а $$ _=_$$, тогда $$ (_-_)=(_-_)= Delta T$$.
$$ Delta _= Delta _+_^<text>=-<displaystyle frac>nu RDelta T=-(<displaystyle frac>+1)nu RDelta T$$.

3) Для адиабатного процесса $$ 3-1$$ имеем (по определению адиабатного процесса): $$ Delta _=0$$.

Сложим полученные результаты и получим ответ:

Или окончательно для гелия:

В проточном калорифере исследуемый газ пропускают по трубопроводу и нагревают электронагревателем (см. рис. $$ 25$$). При этом измеряют количество газа, пропускаемого через трубопровод в единицу времени, и температуру газа перед и за нагревателем. При продувании воздуха в калориметре температура за нагревателем оказалось на величину $$ Delta Т=5$$ К выше, чем перед нагревателем. Массовый расход воздуха $$ _=720$$ кг/ч. Определить мощность нагревателя $$ N$$. Считать, что вся теплота, выделяемая нагревателем, отдаётся газу.

Рассмотрим часть газа, находящегося в трубе в той части, где расположен нагреватель (между сечениями $$ 1$$ и $$ 2$$) (рис. $$ 26$$). Первый термометр $$ left(_right)$$ находится перед рассматриваемой областью, а второй $$ left(_right)$$ за ней.

Запишем первый закон термодинамики для выделенной части газа:

Теперь рассмотрим подробнее каждое слагаемое в этом уравнении.

Количество теплоты, получаемое газом от нагревателя за время $$ Delta t$$, можно записать так:

$$ Delta Q=N Delta t$$.

Изменение внутренней энергии для $$ Delta nu $$ молей воздуха, прошедших через выделенную область за время $$ Delta t$$, определяется выражением

Заметим, что `A_1^’ 0$$ (газ в области расширяется).

Процесс совершения работы слева идёт при постоянной температуре $$ _$$ и постоянном внешнем давлении `p_1`. Совершение этой работы приводит к введению в рассматриваемую область дополнительно $$ Delta _$$ моль газа (показан как закрашенный участок справа от сечения $$ 1$$), занимающих объём $$ Delta _$$. Для $$ _^<text>$$ получаем:

Процесс совершения работы справа идёт при постоянной температуре $$ _$$ и постоянном внешнем давлении `p_1`. Совершение этой работы приводит к выведению из рассматриваемой области объёма газа $$ Delta _$$ моль газа (показан на рисунке выделенным объёмом справа от сечения $$ 2$$), занимающих объём $$ Delta _$$. Для $$ _^<text>$$ получаем:

При стационарном процессе нагрева воздуха количество вошедшего воздуха равно количеству вышедшего: $$ Delta _= Delta _= Delta nu $$. Тогда работа $$ ^<text>$$ равна

С учётом вышеизложенного перепишем первой закон термодинамики для рассматриваемой ситуации:

Любопытно заметить, что процесс нагрева воздуха проходит так, что его описание совпадает с процессом изобарного нагрева.

Теперь подробнее остановимся на массовом расходе воздуха $$ _$$.

Откуда получаем ответ:

С идеальным одноатомным газом проводят циклический процесс $$ 1–2–3–1$$, состоящий из адиабатического расширения $$ 1–2$$, расширения в процессе $$ 2–3$$, в котором теплоёмкость газа оставалась постоянной, и сжатия в процессе $$ 3–1$$ с линейной зависимостью давления от объёма (см. рис. $$ 27$$). Известно, что связь между температурами и объёмами в промежуточных состояниях $$ 1$$, $$ 2$$ и $$ 3$$ выражается соотношениями: $$ _=2_=_$$, $$ _=4_$$. Найдите молярную теплоёмкость газа в процессе $$ 2–3$$, если работа, совершённая над газом в цикле, составляет $$ 7/15$$ от работы, совершённой над газом в процессе $$ 3–1$$.