Все формулы равностороннего треугольника

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Все свойства и формулы прямоугольного треугольникаСкачать

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:Запомни: все формулы для площади треугольникаСкачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

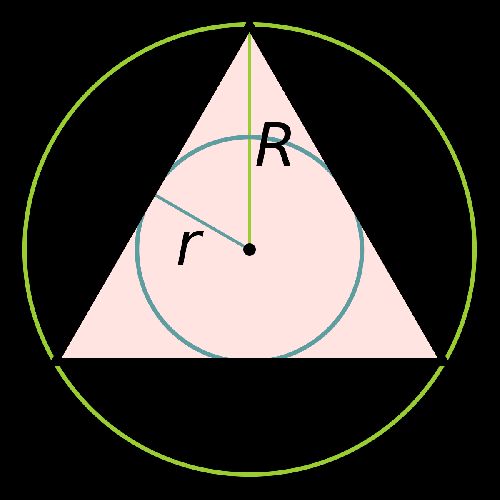
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Видео:Формулы для равностороннего треугольника.Скачать

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Правильный треугольник. Площадь правильного треугольника

Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.

Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.

Пусть сторона правильного треугольника равна .

Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .

Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.

. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Задача решается в одну строчку. Радиус вписанной окружности .

. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .

Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.

. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.

Радиус окружности, описанной вокруг правильного треугольника, равен .

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Правильный треугольник

Средняя оценка: 4.6

Всего получено оценок: 79.

Средняя оценка: 4.6

Всего получено оценок: 79.

Правильный треугольник имеет много специфических свойств, которые значительно упрощают решение задач. Поэтому имеет смысл поговорить о каждом из этих свойств, дабы облегчить решение задач.

Видео:Площадь равностороннего треугольникаСкачать

Определение

Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам. Правильный треугольник еще называют равносторонним. О формулах правильного треугольника, и о том, как производить по ним различные вычисления – поговорим ниже.

Рис. 1. Правильный треугольник.

Видео:Площадь равностороннего треугольника #егэ #математика #геометрия #треугольникСкачать

Формулы правильного треугольника

Почти все формулы вытекают из утверждения о том, что правильный треугольник имеет 3 угла по 60 градусов и 3 одинаковые стороны.

Площадь

Начнем с формулы площади.

Равносторонний треугольник любой высотой делится на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для нахождения площади правильного треугольника.

Рис. 2. Рисунок к доказательству.

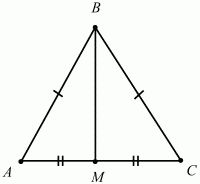
В прямоугольном треугольнике АВМ катет ВМ можно выразить через синус угла ВАМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет ВМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.

С другой стороны синус 60 градусов заранее известнее и равен $sqrt over 2$ . Значит можно выразить значение АМ:

Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.

Тогда формула будет выглядеть следующим образом:

Теперь вспомним классическую формулу площади треугольника:

$S= h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. В заданном треугольнике это будет выглядеть следующим образом:

Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.

Только в правильном треугольнике возможно нахождение площади через значение одной стороны.

Периметр

Периметр найти ещё проще, так как это сумма всех сторон треугольника, а они все равны между собой, то:

Подобный подход, где приравниваются стороны или используются свойства медиан и биссектрис равностороннего треугольника, часто используется при решении подобных задач. У правильного треугольника нет и не может объема, так как это плоская фигура. У нее два характеризующих понятия: площадь и периметр.

В равностороннем треугольнике каждая биссектриса совпадает с медианой и высотой. Также совпадают и точки пересечения этих отрезков. Получившаяся точка зовется центром фигуры.

Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Что мы узнали?

Из статьи мы узнали, что у правильного треугольника все стороны и углы равны между собой. Мы узнали о свойствах биссектрисы, медианы и высоты – в правильном треугольнике это будет одна и та же линия. Ее можно проводить от любой вершины.

🎥 Видео

Задача, которую боятсяСкачать

Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Равносторонний треугольник в окружностиСкачать

Быстрый разбор всех формул равностороннего треугольникаСкачать

ПЛОЩАДЬ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА за 20 секунд!Скачать

№489. Докажите, что площадь равностороннего треугольника вычисляется по формуле, где а — сторонаСкачать

ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Как найти площадь треугольника без формулы?Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Все свойства равностороннего треугольника #shortsСкачать

Как найти сторону равностороннего треугольника #shorts | ЕГЭ 2022 по профильной математике | ЭйджейСкачать