Задача имеет четыре действительных решения (рис. 2.11) и четыре мнимых.
Здесь также применяем свойства циклиды Дюпена. Задача сводится к предыдущей, когда мы имели дело с двумя точками.
В данной задаче для нахождения точек касания А 1 и А 2 строим три конуса (рис. 2.12): два из них касаются двух заданных сфер и проходят через данную точку О 3 , а третий конус является касательным к обеим данным сферам.
Затем, согласно приведенному в разделе 2.1 алгоритму, находим точки касания А 1 и А 2 с данными сферами плоскости, проходящей также и через точку О 3 . Три найденные точки задают касательную к данным сферам и проходящую через точку О 3 плоскость.
После этого определяем положение осей i и j циклиды Дюпена. Плоскость симметрии Д°, содержащая искомые центры очерковых окружностей, проходит через ось j перпендикулярно оси /. В этой плоскости находим центры очерковых окружностей как точки пересечения прямых Д° (см. рис. 2.10) с О 1 0 ю и O^Cf 2 . Сама теория построения представлена в разделе 2.1.
На рис. 2.12, так же как и в предыдущей задаче, получаем известный очерк циклиды Дюпена.
Как видим, пока что теория свойств циклиды Дюпена для всех рассмотренных вариантов задачи Аполлония работает безошибочно.
Видео:КАСАЮЩИЕСЯ ОКРУЖНОСТИ. # ЕГЭ 2023Скачать

Окружность, касающаяся трех прямых
Рассмотрим эту задачу как задачу Аполлония с окружностями бесконечно большого радиуса (рис. 2.13, а). По сути, в данном примере заданы три фронтально проецирующие плоскости: Г, X и А.
Здесь снова используем свойство 8 и его следствие. Касательные конусы для нахождения точек касания в этой задаче вырождаются в прямые а, Ь, с пересечения данных плоскостей. Эти прямые содержат и искомые точки «касания» трех данных плоскостей четвертой.
Только следует иметь ввиду не действительную плоскость касания, а несобственную.
Таким образом, первые три точки мы имеем. Для нахождения следующих трех точек, поступаем, как в работе [2]: строим дополнительные три «сферы», увеличивая или уменьшая их «радиус» на одну и ту же величину 5 (см. рис. 2.13). Эти «сферы» также имеют «касательные конусы», вырожденные в прямые, параллельные а, b и с. Проведя через соответствующие параллельные прямые плоскости, по сути являющиеся биссекторными, получим «ось» циклиды Дюпена (в данном примере она обозначена буквой О), выродившуюся в цилиндр вращения. Соединив точку О с «центрами» данных сфер, а по сути проведя из О перпендикуляры к прямым а, Ь, с, получим точки касания.
Следует отметить, что при таком задании «сфер», при разном условии касания мы получим четыре действительных цилиндра вращения (рис. 2.13, б) и четыре мнимых.
Таким образом, мы рассмотрели частный случай получения циклиды Дюпена, когда она вырождается в цилиндр вращения.
Если плоскости Г, X и А будут пересекаться в одной точке, мы получим циклиду Дюпена в виде конуса вращения.
Видео:Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Постройте окружность данного радиуса, касающуюся двух данных окружностей.
Видео:Задача о радиусе окружности, касающейся трёх полуокружностейСкачать

Ваш ответ
Видео:Касающиеся окружности.Скачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,804
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:ОКРУЖНОСТЬ (внешне касающиеся окружности с разными радиусами-хорды) ЧАСТЬ 27Скачать

С помощью циркуля и линейки постройте окружность, касающуюся двух данных окружностей, причём одной из них — в данной точке.
Предположим, что нужная окружность S построена. Пусть A — данная точка на данной окружности S1, а l — общая касательная к окружностям S и S1, проходящая через точку A. Если S2 — вторая данная окружность, то окружность S касается окружности S2 и прямой l в данной на ней точке A.
Таким образом, задача сводится к построению окружности, касающейся данной окружности (S2) и прямой (l) в данной на ней точке (A).
Для этого построим касательную к окружности S2, параллельную прямой l, т.е. касательной к окружности S1, проведённой в точке A. Ограничимся рассмотрением случая, когда данные окружности лежат по разные стороны от прямой l. Если B — полученная точка касания на S2, то точка M пересечения прямой AB с окружностью S2 есть точка касания искомой окружности с окружностью S2. Если O1 и O2 — центры окружностей S1 и S2 соответственно, то пересечение прямых O2M и O1A даёт центр O искомой окружности.
В рассматриваемом случае задача имеет два решения (внешнее и внутреннее касание окружностей S и S2).
💥 Видео
Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать

Интересная задача о трёх попарно касающихся окружностяхСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

ЕГЭ Задание 16 Две касающиеся окружностиСкачать
3.2. Окружности и их элементы. Касающиеся окружности.Скачать

10 класс, 11 урок, Числовая окружностьСкачать

ЕГЭ Задание 16 Внутреннее касание двух окружностейСкачать
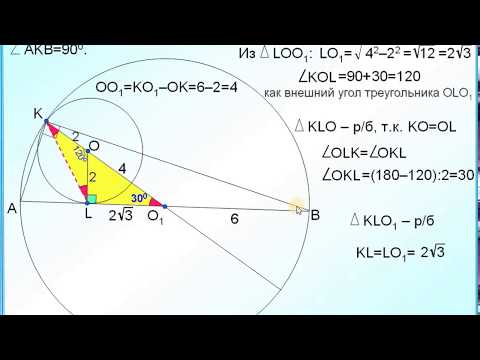
Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Параметр. Серия 13. Решение задач с окружностями. Касание двух окружностейСкачать

Геометрия 16-09. Взаимное расположение двух и более окружностей. Задача 9Скачать

ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Профильный ЕГЭ 2024. Задача 16. Касающиеся окружностиСкачать

С4, егэ. Задача про три касающиеся друг друга окружностиСкачать

1 2 4 сопряжение окружностейСкачать



