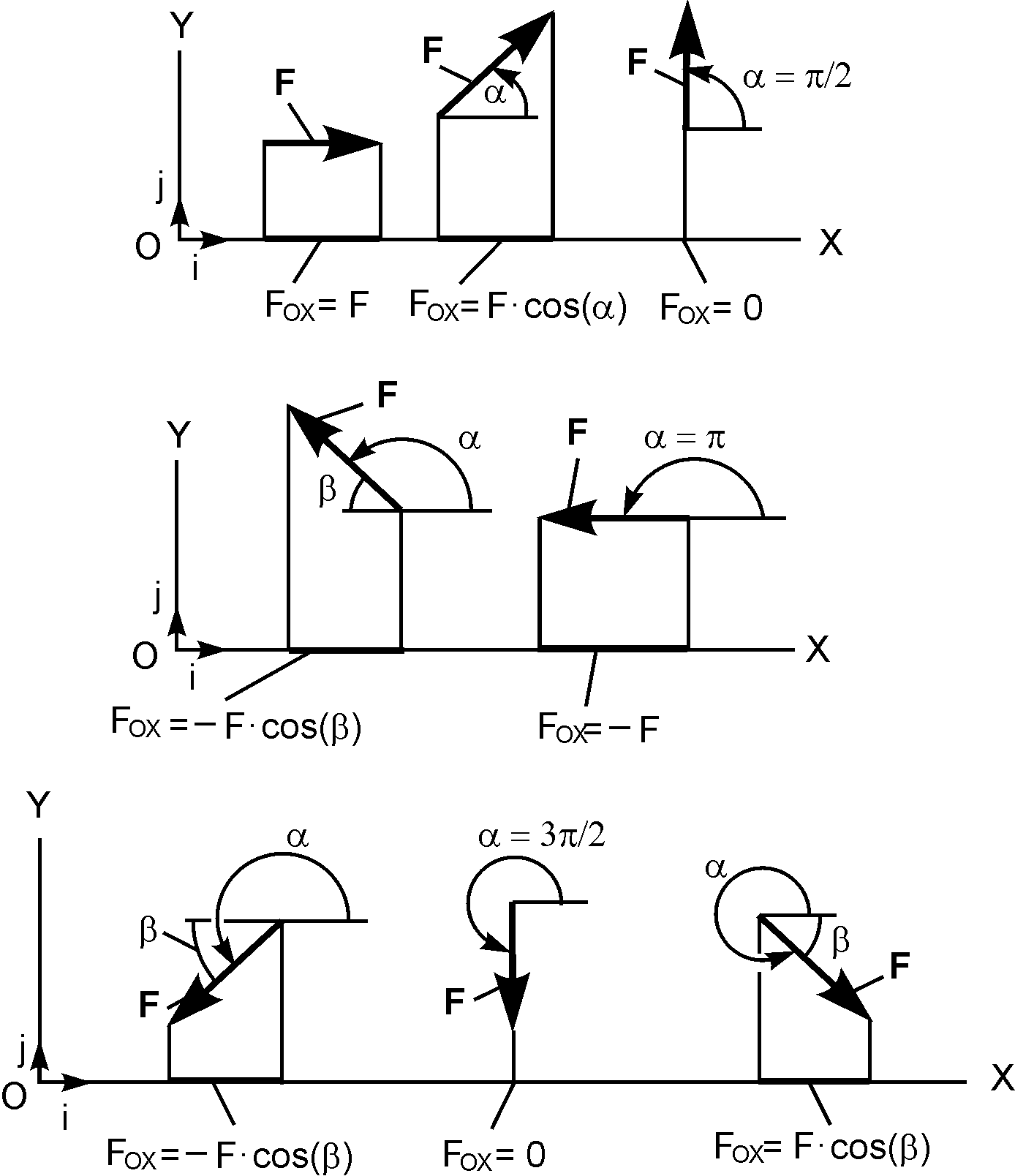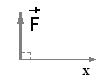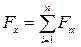Найти косинус угла между вектором силы f 3j и осью ох

Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Найти косинус угла между вектором силы f 3j и осью ох

1. Система сходящихся сил.

1.3. Сложение и разложение сходящихся сил в плоскости.

1.3.1. По заданным проекциям силы F на оси координат: F_x = 20Н, F_y = 25Н и F_z = 30 Н, определить модуль этой силы. (Ответ 43,9)

1.3.2. Определить косинус угла между вектором силы F и осью коорди­нат O_z, если сила (Н)
F = 3 i + 4j + 5k. (Ответ 0,707)

1.3.3. Определить косинус угла между вектором силы (Н) F = 3i + 2,45j + 7k и осью координат О_х. (Ответ 0,375)

1.3.4. Модуль равнодействующей R пространст­венной системы сходящихся сил равен 150Н. Определить ее проекцию на координатную ось О_у, если даны углы α = 30°, β = 60°. (Ответ 65)

1.3.5. Определить модуль равнодействующей сил F₁ = 12 Н, F₂ = 10 Н и F₃ = 9 Н, приложенных в точке А , как показано на рисунке. (18,0)

1.3.6. Определить модуль равнодействующей сил F₁ = 15Н, F₂ = 20Н и F₃ = 25Н. Углы, образованные линиями действия сил F₁, и F₃ с осями координат, заданы: α = 60° и β = 45°. (Ответ 50,5)

1.3.7. Направление равнодействующей трех сил R = 33,8 Н задано косинусами направляющих углов: cos(R^x) = 0,325; cos (R^y) = 0; cos (R^z) = 0,946. Проекции сил F ₁ и F₂ на координатные оси соответственно равны: F_lx = 7 Н; F_1y = 10 Н; F_1z=0; F_2x = — 5 Н; F_2y = 15Н; F_2z = 13 Н. Определить модуль силы F₃. (Ответ 32,6)

1.3.8. Определить модуль равнодействующей трех сходящихся сил, если заданы их проекции на оси координат: F_lx = 7 Н; F_1y= 10Н; F_1z = 0; F_2x = -5 Н; F_2y = 15Н; F_2z = 12 Н; F_3x = 6 Н; F_3y = 0; F_3Z = -6 Н. (Ответ 26,9)

1.3.9. Две силы (Н) F₁ = 5i + 7j + 9k и F₂ = 4i + 9j + 11k приложены в центре О системы прямоугольных координат О_хуz. Определить мо­дуль равнодействующей силы. (Ответ 27,1)

1.3.10. Определить модуль равнодействующей трех сходящихся сил, если заданы их модули
F₁ = 5кН, F₂ = 12кН, F₃ = 9кН и угол β =60°. (Ответ 20,9)

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Онлайн калькулятор. Вычисление угла между векторами

Этот онлайн калькулятор позволит вам очень просто найти угол между двумя векторами (косинус угла между векторами) для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между векторами и закрепить пройденный материал.

Видео:Угол между векторами. 9 класс.Скачать

Калькулятор для вычисления угла между векторами

Инструкция использования калькулятора для вычисления угла между векторами

Ввод даных в калькулятор для вычисления угла между векторами

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления угла между векторами

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Теория. Вычисление угла между векторами

Угол между двумя векторами a и b можно найти использовав следующую формулу:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Угол между векторами | МатематикаСкачать

Сумма проекций сил на ось

Проекция силы на ось – это алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и вектором силы (т.е. это отрезок, откладываемый силой на соответствующие оси. Рисунок 1.13):

Проекция силы на ось может быть положительной, рис. 1.13а ( 0 ≤ α β = π/2) и отрицательной, рис. 1.13в ( π/2 P_z = P ∙ sinα;
P_x = (P ∙ cosα)cosβ;
P_y = (P ∙ cosα)cosγ = P ∙ cosα ∙ cos(90 o — β).

усть линия действия силыF лежит в плоскости OXY (рис. 1.25).

По правилу параллелограмма разложим эту силу на составляющие силы F_ОХ, F_OY по координатным осям OX и OY. Силы F_OX, F_OY называют компонентами силы F по координатным осям OX и OY. Очевидно векторное равенство

Спроецируем компоненты F_OX, F_OY силы F на координатные оси и получим скалярные величины F_OX, F_OY, которые называют проекциями силы на оси OX и OY.

Компоненты силы и её проекции на координатные оси связаны равенствами: F_OX = iF_OX; F_OY = jF_OY.

Проекция силы на ось – скалярная величина, равная взятой со знаком плюс или минус длине отрезка, заключённого между проекциями на ось начала и конца силы.

усть в пространстве в системе отсчёта OXYZ задана силаF, (рис. 1.26).

Используя правило параллелепипеда, разложим силу F на компоненты F_OX, F_OY, F_OZ. По правилу сложения векторов справедливо равенство

Последнее равенство представляет собой формулу разложения силы на составляющие силы по координатным осям.

Проекция силы на координатную ось равна произведению модуля силы на косинус угла, составленного направлениями силы и оси.

Модуль силы через её проекции определяют по формуле

.

Направляющие косинусы, используемые для определения направления силы, находят по формулам:

Если рассматривается сила, лежащая в плоскости OXY, то применяются формулы:

;

ри определении проекции силы на ось возможны следующие частные случаи (рис. 1.27).

Анализ частных случаев определения проекции силы на ось позволяет сделать следующие выводы: 1) если сила и ось направлены в одну полуплоскость, то проекция силы на ось положительна; 2) если сила и ось направлены в разные полуплоскости, то проекция силы на ось отрицательна; 3) если сила и ось взаимно перпендикулярны, то проекция силы на ось равна нулю; 4) если сила и ось параллельны, то сила проецируется на ось в натуральную величину с соответствующим знаком.

При решении задач статики рекомендуется вычислять абсолютное значение проекции как произведение модуля силы на косинус острого угла между линией действия силы и осью, определяя знак проекции непосредственно по чертежу.

инженерной практике принято использовать заданный угол и выражать через него проекции силы на оси (рис. 1.28).

Проекцией силы на плоскость OXY называется вектор F_OXY, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 1.29).

Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только модулем, но и направлением по плоскости OXY. По модулю F_ОXY = F·cos(), где  – угол между направлением силы F и её проекцией F_OXY,

В некоторых случаях для нахождения проекции силы на ось бывает удобнее найти сначала её проекцию на плоскость, в которой эта ось лежит, а затем найденную проекцию силы на плоскость спроецировать на данную ось. Тогда:

Решение задач на равновесие сходящихся сил с помощью построения замкнутых силовых многоугольников сопряжено с громоздкими построениями. Универсальным методом решения таких задач является переход к определению проекций заданных сил на координатные оси и оперирование с этими проекциями. Осью называют прямую линию, которой приписано определенное направление.

Проекция вектора на ось является скалярной величиной, которая опреде­ляется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.

Проекция вектора считается положительной, если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной, если направление от начала проекции к ее концу противоположно положительному направлению оси.

Таким образом, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.

Рассмотрим ряд случаев проецирования сил на ось:

Вектор силы F (рис. 15) составляет с положительным напра­влением оси х острый угол .

Чтобы найти проекцию, из начала и конца вектора силы опускаем перпендикуляры на ось oх; получаем

Проекция вектора в данном случае положительна

Сила F (рис. 16) составляет с положительным направлением оси х тупой угол α.

Тогда F_x = F cos α, но так как α = 180 0 – φ,

Проекция силы F на ось oх в данном случае отрицательна.

Сила F (рис. 17) перпендикулярна оси oх.

Проекция силы F на ось х равна нулю

Силу, расположенную на плоскости хоу (рис. 18), можно спроектировать на две координатные оси ох и оу.

Силу F можно разложить на составляющие: F_x и F_y. Модуль вектора F_x равен проекции вектора F на ось ox, а модуль вектора F_y равен проекции вектора F на ось oy.

Модуль силы можно найти по теореме Пифагора:

Проекция векторной суммы или равнодействующей на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

Рассмотрим сходящиеся силы F₁, F₂, F₃, и F₄, (рис. 19, а). Геометрическая сумма, или равнодействующая, этих сил F определяется замыкающей стороной силового многоугольника

Опустим из вершин силового многоугольника на ось x перпендикуляры.

Рассматривая полученные проекции сил непосредственно из выполненного построения, имеем

где n – число слагаемых векторов. Их проекции входят вышеуказанное уравнение с соответствующим знаком.

В плоскости геометрическую сумму сил можно спроецировать на две координатные оси, а в пространстве – соответственно на три.

🎬 Видео

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

Построение проекции вектора на осьСкачать

Косинус угла между векторами. Коллинеарность векторовСкачать

Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

§7 Направляющие косинусы вектораСкачать

4.2 Проекция силы на ось координатСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Как находить угол между векторамиСкачать

Проекция силы на осьСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Урок 9. Проекции вектора на координатные осиСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Задача 3. Найти косинус угла между векторами.Скачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

Математика это не ИсламСкачать