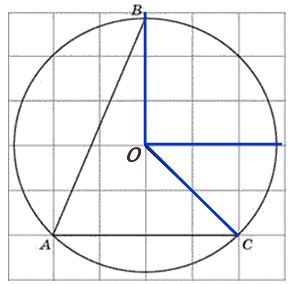
Найти градусную меру угла в окружности на клетчатой бумаге (7 видео)

Найти градусную меру угла в окружности на клетчатой бумаге

Задание 7. На клетчатой бумаге с размером клетки 1х1 изображён вписанный в окружность угол ABC . Найдите его градусную величину.

Угол ABC является вписанным углом, градусная мера которого, в 2 раза меньше градусной меры дуги, на которую он опирается, т.е. градусной меры дуги AC. В свою очередь, на дугу AC опирается центральный угол (см. рисунок), величина которого 90 градусов (видно из рисунка). Тогда градусная мера дуги также будет 90 градусов и угол ABC равен 90:2=45 градусов.

Видео:Градусная мера угла, изображенного на клетчатой бумагеСкачать

На клетчатой бумаге изображён вписанный угол

Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.

Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?

Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?

Начнём с самого простого. Чему равен данный угол?

Конечно же, 90 градусам.

Чему равен этот угол?

Понятно, что 45 градусам.

Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).

225 градусов (180 + 45 или 360 – 135).

Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.

Ещё раз напомню основное свойство вписанного угла.

«Вписанный угол равен половине центрального,

опирающегося на ту же дугу»

27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.

Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.

Построим центральный угол соответствующий дуге ВС:

Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:

По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).

27887. Найдите величину угла ABC . Ответ дайте в градусах.

27888. Найдите величину угла ABC. Ответ дайте в градусах.

27889. Найдите величину угла ABC . Ответ дайте в градусах.

27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.

Нужно знать свойство вписанного угла (обязательно).

Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.

На этом всё. Успеха Вам!

С уважением, Александр Крутицких

Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Найти градусную меру угла в окружности на клетчатой бумаге

На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.

Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: &angle;ABC = 72° : 2 = 36°.

На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.

Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:

Найдите угол ABC. Ответ дайте в градусах.

Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.