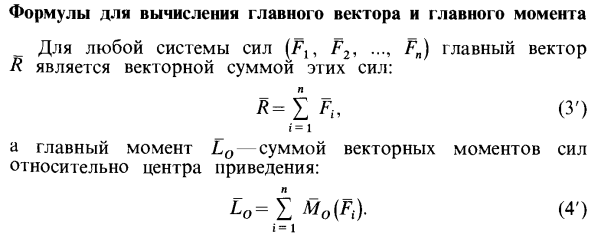
Найти главный вектор системы сил если r 2м (5 видео)

Формулы для вычисления главного вектора и главного момента

Содержание

Формулы для вычисления главного вектора и главного момента
Тема 1.4. Система произвольно расположенных сил
Задание на расчетно-графическую работу №2. Фрагмент методички с заданиями, которые задают где-то на Дальнем Востоке. Задания не являются оригинальными и взяты из другой методички. Образцы оформления здесь
Гарантии (в плюсиках тоже есть текст)
💡 Видео

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Формулы для вычисления главного вектора и главного момента

Для любой системы сил Г1ЭГ2, FN главным вектором R является векторная сумма этих сил. 3 i = 1. Основным моментом Эо является сумма векторных моментов силы относительно центра торможения. 4 нынешний век i = 1 гора R изображается геометрически как замкнутый силовой полигон, построенный на заданной силе.

Поскольку угол поворота увеличивается со временем, он становится положительным, когда тело вращается против часовой стрелки, и отрицательным, когда тело вращается по часовой стрелке.Каковы необходимые и достаточные условия приведения тела в неупорядоченное состояние. Людмила Фирмаль

Для любой пространственной системы сил, которую мы получаем, мы проецируем обе стороны векторного уравнения 3 на координатные оси х = я х, .= Я. е лх, е лх. 5 = 1 1 = 1 1 = 1 Проекция определяет Косинус модуля основного вектора и его угол к координатным осям. СО8 х, ЛЯ = , СО8 6ЛЛ =А С05 все =. 6 Главный момент Lo геометрически изображается в виде замкнутого векторного многоугольника, построенного на векторном моменте силы относительно приведенного Центра.

Обе части векторного уравнения 4 проецируются на декартову ось, используя соотношение между моментом силы относительно оси и проекцией этого момента вектора силы относительно точки на оси. LOx = Lx = E WX F, = E y Fiz z. fiy. 1 = 1 1 = 1 П0. = Ly = E L DG = E Zifix X. физ я = 1 я = л Кровать Loz = Л. = ЕК Фи = Е я = Л 1 = 1 Дж 7 Косинус угла между модулем и осью основного момента Координаты равны потому что Х, ло ЛК ЛО, потому что г, о лы ЛО, Ц0 Ео = В1 В0. 8.

В равновесном состоянии сила, действующая на твердое тело в равновесии на шероховатой поверхности объекта на равновесной шероховатой поверхности, есть еще неизвестная сила реакции, то есть сила трения на шероховатой поверхности. Людмила Фирмаль

Ось Oz перпендикулярна плоскости действия силовой плоской системы, а оси Ox и Oy в силовой плоскости, главный вектор R находится в плоскости Oxu, а следовательно, и в случае силовой плоской системы 9. ГХ = исправить е, ры = И. Ли, L2eO Л = Vy1 + ч, потому что Х, АР = х, С08 Я = Я, Д. Главный момент плоской системы сил перпендикулярен основному вектору, а следовательно, параллелен оси Oz. И затем… Lx = 0, Ly = 0, L0 = L, = ЗД = Z A 0 f , 10 i = 1 i = 1. Где Ло является ключевым моментом алгебраических.

Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Приведение системы сил к простейшему видуСкачать

Тема 1.4. Система произвольно расположенных сил

§1. Приведение пространственной системы сил к данному центру

Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.

Теорема о параллельном переносе силы. Для переноса действующей на абсолютно твердое тело силы

из точки А (рис. 1, а) в точку О прикладываем в точке О силы и

. Тогда сила окажется приложенной в точке О и к ней будет присоединена пара () с моментом , что можно показать еще так, как на рис. 1, б. При этом .

Рис.1. Произвольной плоской системой сил

Рассмотрим теперь твердое тело, на которое действует какая угодно система сил

, ,…, (рис. 2, а). Выберем произвольную точку О за центр приведения и перенесем все силы системы в этот центр, присоединяя при этом соответствующие пары. Тогда на тело будет действовать система сил

. приложенных в центре О, и система пар, моменты которых будут равны ,

Силы, приложенные в точке О, заменяются одной силой , приложенной в той же точке.

Чтобы сложить все полученные пары, надо геометрически сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой или

Величина , равная геометрической сумме всех сил, называется главным вектором системы;

величина , равная геометрической сумме моментов всех сил относительно центра О,

называется главным моментом системы относительно этого центра.

Рис.2. Система сил

Таким образом мы доказали следующую теорему, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой

, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом , равным главному моменту системы относительно центра О (рис. 2, б).

Векторы и обычно определяют аналитически, т.е. по их проекциям на оси координат.

Выражения для R_x, R_y, R_z нам известны. Проекции вектора на оси координат будем обозначать M_x, M_y, M_z. По теореме о проекциях суммы векторов на ось будет

Окончательно для определения проекций главного вектора и главного момента получаем формулы:

При этом главный вектор пространственной системы сил: R₀ = ΣP_i отличается от главного вектора плоской системы сил только наличием третьей компоненты, поэтому его модуль будет равен:

Главный момент пространственной системы сил: M₀ = ΣM₀(P_i) — это вектор, модуль которого находится аналогично:

где M_x , M_y , M_z — суммы моментов всех сил системы относительно соответствующих осей.

В зависимости от значений главного вектора и главного момента, а также от их взаимного расположения возможны следующие варианты приведения пространственной системы сил:

1) R₀ = 0, M₀ = 0 — система сил находится в равновесии;

2) R₀ = 0, M₀ ≠0 — система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения;

3) R₀ ≠0, M₀ = 0 — система эквивалентна равнодействующей R, равной и эквивалентной главному вектору системы R₀ , линия действия которой проходит через центр приведения: R = R₀, R

4) R₀ ≠0, M₀ ≠0 и R₀ ⊥ M₀ — система эквивалентна равнодействующей R, равной главному вектору системы R₀ , ее линия действия проходит на расстоянии d = |M₀|/ R₀ от центра приведения.

5) R₀ ≠ 0, M₀ ≠0 и главный вектор R₀ неперпендикулярен главному моменту M₀ — система эквивалентна скрещивающимся силам или динаме.

При этом скрещивающимися называются силы, которые непараллельны и не лежат в одной плоскости, а динамой называется система, состоящая из силы и пары сил, плоскость которой перпендикулярна этой силе.

Динама, приложенная к твердому телу, стремится вызвать его винтовое движение, которое представляет совокупность вращательного и поступательного движений.

Примечание: Для пространственной системы сил, как и для плоской, справедлива следующая Теорема Вариньона: Момент равнодействующей пространственной системы сил относительно произвольного центра (оси) равен геометрической (алгебраической) сумме моментов всех сил этой системы относительно данного центра (оси).

§2.Условия равновесия произвольной пространственной системы сил

Произвольную пространственную систему сил, как и плоскую, можно привести к какому-нибудь центру О и заменить одной результирующей силой и парой с моментом . Рассуждая так, что для равновесия этой системы сил необходимо и достаточно, чтобы одновременно было R = 0 и M_о = 0. Но векторы

Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать

Задание на расчетно-графическую работу №2. Фрагмент методички с заданиями, которые задают где-то на Дальнем Востоке. Задания не являются оригинальными и взяты из другой методички. Образцы оформления здесь

Задача 1. Пример
Для балок построить эпюры поперечных сил и изгибающих моментов. Данные для задачи своего варианта взять из таблицы 5

Задача 2. Пример
Определить аналитическим способ усиления в стержнях АВ и ВС заданной стержневой системы (рис. 2). Исходные данные для задачи своего варианта взять из таблицы 2

Задача 3. Пример
Определить реакции опор балки нагруженной как показано на схеме (рис. 5). Исходные данные приведены в таблице 3

Задача 3. Схемы. Пример
Определить реакции опор балки нагруженной как показано на схеме (рис. 5). Исходные данные приведены в таблице 3

Задача 4. Пример
Определить положение центра тяжести сложной фигуры, ее сечение имеет вид (см. рис. 8). Данные для задачи своего варианта взять из таблицы 4

Задание №18. Пример

1. Определить положение расчетного центра тяжести фигуры, размеры указаны в мм.
2. Вырезать фигуру из плотной бумаги.
3. Методом подвешивания определить опытное положение центра тяжести.
4. Сравнить полученные результаты

4.4. Пример
Чему равно наибольшее касательное напряжение в толстой части ступенчатого вала, если в тонкой части оно 135 МПа?
Ответ: τ_max2=80 МПа

10. Поезд весом 3000 кН идет со скоростью 36 км/ч. Сила сопротивления движению составляет 0,005 веса поезда. Определить полезную мощность тепловоза. Движение прямолинейное по горизонтальному пути

Вариант 5 Пример
Определить проекцию равнодействующей системы сил на ось 0у F₁=10 кН F₂=8 кН F =20 кН
Как направлен вектор равнодействующей силы, если известны величины его проекции? 11Н 23,59 Н Определить αx
Какой вектор силового многоугольника является равнодействующей силой?
Груз F находится в равновесии. Указать, какой из силовых треугольников для шарнира В построен верно.
Груз F находится в равновесии. Указать, какие условия для точки равновесия В записаны верно

5.4.7 Пример
В центре приведения О главный вектор R=5 Н и главный момент МO=25 Нм. Определить значение главного момента в центре приведенияя А, если ОА=1 м

5.4.8 Пример
При приведении системы сил к центру О получены главный вектор R=10 Н и главный момент М0=20 Нм. Определить модуль главного момента в центре приведения А, если расстояние ОА=2 м

ЗАДАЧА №12. Пример
Стержень AB длиной 60 см скользит своими концами и по сторонам угла. Определить скорости точек В и С, а также угловую скорость стержня, если скорость точки А равна 10 см/с

ЗАДАЧА 8. Пример
Для изображенной на схеме передачи определить вращающий момент Т₂ на ведомом валу. Исходные данные: мощность на ведущем валу Р₁=8 кВт; угловая скорость ведущего вала ω₁=40 рад/с; коэффициент полезного действия передачи η=0,97; передаточное число передачи u=4

Промежуточная контрольная работа по Технической механике. Вариант 10. Пример
• Задание №1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях.
• Задание №2. Груз подвешен на стержнях и канатах находится в равновесии. Определить усилия в стержнях.
• Задание №3. Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом

ВАРИАНТ 6. Задача 1 Пример
Определить реакции стержней кронштейна АВС, изображенного на схеме (рис.5), если сила F направлена вертикально вниз.
Стержни АВ и ВС считать жесткими, невесомыми. Точки А, В, С — цилиндрические шарниры.
Значение силы F, углы α, β сведены в таблице

2. Пример
В соединениях 1 и 2 кронштейн закреплен на колонне болтами, установленными в отверстиях с зазором. Какой из вариантов, при прочих равных условиях, рациональнее, если в качестве критерия рациональности принять нагрузочную способность

Задание 3.
К тормозному колесу диаметром 370 мм, жестко посаженному на вал двигателя, прижимают с помощью рычага тормозную колодку силой F=180 Н.
Вал вращается при этом равномерно и делает 1950 об/мин.
Коэффициент трения между колесом и колодкой 035. Опрсдедкть мощность (в кВт и л.с.) развиваемую двигателем, если потери на трение и нем составляют 15%

Колесный трактор имеет двигатель, развивающий максимальную Мощность 62.5 кВт КПД трансмиссии трактора 0.72 масса трактора вместе с перевозимым грузом 2250 кг.
Определить наибольшую скорость движения в км/ч, с которой может двигаться трактор по асфальтированной дороге, коэффициент трения равен 0.18

КОНТРОЛЬНАЯ РАБОТА № 1. Вариант 3

Задача 1. Пример Определить реакции стержней, удерживающих грузы F₁ и F₂ . Массой стержней пренебречь. F₁=0,6 кН F₂=0,4 кН
Задача 2. Пример Определить реакции опор двухопорной балки. q=10 Н/м F=16 Н М=14 Нм
Задача 3. Пример Определить центр тяжести плоской фигуры
Задача 4. Пример Скорость самолёта при отрыве от взлётной полосы должна быть 300 км/ч. Определить минимальную длину взлётной полосы, необходимую для того, чтобы лётчик при разгоне испытывал перегрузку, не превышающую его утроенный вес.
Задача 5. Пример Определить реакции опор балки. F=18 Н q=2 Н/м

Вариант 1 Пример
1. Определить проекции силы F=14 Н на оси координат.
2. Определить моменты сил относительно указанной точки. Дано: F₁=25 Н, F₂=14 Н, F₃=28 Н, а=20 см, b=50 см.
3. Чему равено модуль силы Р, если её проекции Px=9 Н, Py=-12 Н.
4. Найти моменты сил относительно осей

Тест l-го уровня. Сдвиг, срез, смятие Пример
Во всех заданиях выбрать номер правильною ответа
Задание 1. Если в поперечных сечениях элемента возникает, внутренний силовой фактор — поперечная сила, то такой вид деформации называется: растяжением сдвигом смятием
Задание 2. Поперечная сила действует: в плоскости поперечного сечения бруса перпендикулярно плоскости поперечного сечения бруса вдоль продольной оси бруса
Задание 3. Единица измерения напряжения 1 Па составляет: Н/мм 2 кг/см 2 Н/м 2 (модуль сдвига)

Тест l-го уровня. Сдвиг, срез, смятие Пример
Задание 4. Болт нагружен растягивающей силой F. Рассчитать величину площади смятия, если d=20 мм, h=14 мм, D=36 мм 468 224 1331 703 мм 2
Задание 5. Из условия прочности болта на смятие определить величину допускаемой нагрузки F, если [τ_ср.]=100 МПа, [σ_см]=240 МПа, используя данные задания 4 22,4 кН 84.3 кН 168,7 кН 70,3 кН
Задание 6. Установить соответствие в формуле зависимости между тремя упругими постоянными материала: G = E/2(1-μ) Коэффициент Пуассона Модулем упругости 1-го рода Модулем упругости 2-го рода (модуль сдвига)

Тест. Эпюры балок. Очертания контуров эпюр Пример
Указать соответствие между схемой балки и эпюрами Q и М. Схема ответа

Тест. Эпюры простых балок
Установить соответствие между схемой балки и эпюрами поперечных сил Q и изгибающих моментов М. Схема ответа Q — а) М — б)

Гарантии (в плюсиках тоже есть текст)

Посмотрите на мой сайт. Все виды связи, почта и группа , в ней отзывы реальных людей, вы можете им написать, и, если человек ответит, пообщаться с ним. Может быть знакомого найдете.
Клиент, довольный работой, возвращается еще, приводит друга, заказывает для товарища. Причем чем быстрее он получит качественную работу, тем выше вероятность повторного заказа. Это правило проверено многолетней практикой. Не сомневайтесь. Мой бизнес строится на репутации.