Найти cba в равнобедренном треугольнике

Найти:
Решение:
AC=CB , отсюда следует что данный треугольник равнобедренный (свойство). А значит что .

Сумма углов треугольника равна 180°.
Для равнобедренного треугольника, сумму углов можно представить в таком виде:

Теперь решим данное уравнение:

2) Дано: DB=BC, BA медиана,
Найти : угол СВА
Решение:
DB=BC , отсюда следует что треугольник BCD равнобедренный.
А значит медиана BA является и биссектрисой и высотой (по свойству).
Отсюда следует что: (свойство биссектрисы)
(свойство равнобедренного треугольника)
То есть сумму углов представить можно следующим образом:

Теперь найдем нужный угол:

Остальные треугольники тоже равнобедренные, так что попробуй подумать и решить. Это очень легко.

Видео:№228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°Скачать

Найдите угол CBA на всех рисунках?

Геометрия | 5 — 9 классы

Найдите угол CBA на всех рисунках.

Решить с Дано, найти, решение.

ПОМОГИТЕ заранее спасибо.

1. ΔАВС равнобедренный, значит углы при основании АС равны.

∠СВА = ∠САВ = (180° — 30°) / 2 = 75°

ΔABD — равнобедренный, значит углы при основании AD равны.

∠СВА — внешний, значит равен сумме двух внутренних, не смежных с ним.

∠СВА = ∠BAD + ∠BDA = 140°.

3. ΔBMN равнобедренный, значит углы при основании NM равны.

∠MBN = 180° — (75° + 75°) = 30°

∠CBA = ∠MBN = 30° как вертикальные.

4. ΔABD равнобедренный, ВМ медиана, проведенная к основанию AD, а значит и высота.

∠СВА — внешний для треугольника МВА, значит равен сумме двух внутренних, не смежных с ним.

∠СВА = ∠ВАМ + ∠ВМА = 45° + 90° = 135°

ΔDBC равнобедренный, значит углы при основании СD равны.

∠CDB = 180° — (40° + 40°) = 100°

ВА — медиана равнобедренного треугольника, значит и биссектриса.

∠СВА = ∠CBD / 2 = 100° / 2 = 50°

СК — медиана равнобедренного треугольника CBD, проведенная к основанию BD, а значит и высота.

∠СВА — внешний для треугольника СКВ, значит равен сумме двух внутренних, не смежных с ним.

∠СВА = ∠ВКС + ∠ВСК = 30° + 90° = 120°

ВА — медиана равнобедренного треугольника АСD, проведенная к основанию СD, а значит и высота.

ΔЕBD — равнобедренный, значит углы при основании ЕD равны.

∠ЕBD = 180° — (70° + 70°) = 40°

∠СВА = ∠ЕBD = 40° как вертикальные.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Надо найти угол CBA помогитеееее?

Надо найти угол CBA помогитеееее.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Найдите угол CBA заранее спасибо?

Найдите угол CBA заранее спасибо!

Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

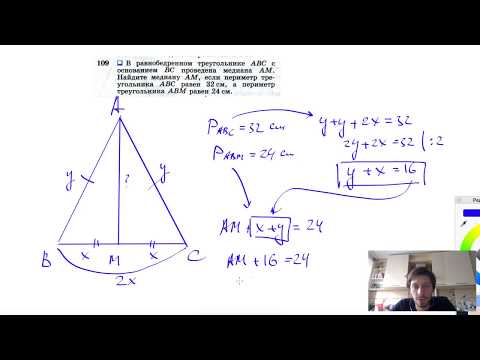
Помогите найти площадь равнобедренногоо треугольника?

Помогите найти площадь равнобедренногоо треугольника.

Если основание равно 12 см а противоположный ему угол = 60 градусов.

Больше данных нет.

Желательно с решением.

Видео:Равнобедренный треугольник. 7 класс.Скачать

Чему равен угол CBA?

Чему равен угол CBA?

Если можно с решением.

Видео:Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

По данным рисунка найти угол B помогите срочно?

По данным рисунка найти угол B помогите срочно!

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Здравствуйте?

Помогите пожалуйста решить задачку по геометрии.

Нужно найти угол CBA.

. Папа решить не смог .

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

У меня 2 задачки для вас))?

У меня 2 задачки для вас)).

1)На рисунке угол ABC = 70 градусов.

Найдите угол AKC

2)Дан прямоугольник ABCD.

Угол CAB = 30 градусов.

Найдите периметр прямоугольника.

(Рисунки во вложениях).

Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

Помогите пожалуйста решить?

Помогите пожалуйста решить.

С рисунком и подробным решением.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Помогите решить задания под номером : 5, 6, 7 Найдите угол CBA ?

Помогите решить задания под номером : 5, 6, 7 Найдите угол CBA .

Решение оформить с подробной записью (Дано, Найти, Решение ).

Видео:№119. В равнобедренном треугольнике DEK с основанием DK=16см отрезок EF— биссектриса,Скачать

По данным рисунка найдите угол 1?

По данным рисунка найдите угол 1.

Вы перешли к вопросу Найдите угол CBA на всех рисунках?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

52 так как угол АКБ 90, АК бессектриса, а парально в 51 так как АК и ВК паралельны, а АК бесектриса и ВК бесектриса, а паралельна в.

Надеюсь на фото все понятно.

Пусть коэффициент пропорциональности равен — х. Тогда составим уравнение. Так как сумма смежных углов равна 180°, получаем : 5х + 13х = 180° 18х = 180° х = 10° Тогда первый угол равен 50°, а второй 130°.

S = a : d 84 : 14 = 6 Ответ : 6.

14 другая сторона. (т. к. Противоположные стороны равны) другие стороны = 98 — 28 : 2 = 35 35 одна, и другая сторона.

Строим линию пересечения двух плоскостей : АМД и ДВЕ. Проводим отрезок АМ. Пересечение линии пересечения плоскостей АМД и ДВЕ и отрезка АМ и даёт искомую точку.

Общаться в чатеДля периметра сначала находим третью противолежащую углу В сторону по теореме косинусов : AC ^ 2 = AB ^ 2 + BC ^ 2 — 2AB * BC * cos B = 64 + 225 — 2 * 8 * 15 * 1 / 2 = 169 = 13 ^ 2 p = AB + BC + AC = 8 + 15 + 13 = 36 м Для площади испо..

Решила на листочке) надеюсь все понятно.

Треугольник атс прямоугольный sin bac = ct / ac = 4 / 16 = 0. 25 проведем высоту ah Δatc = Δahc по гипотенузе и острому углу ac — общая сторона, угол bac = углу bca т. К. углы при основание в равнобедренном треугольнике равны тогда sin bac = sin bc..

Спочатку треба знайти сторону трикутника. А = R(радіус описаного кола) поділити на «корінь з 3 поділити на 3» = 18. Периметр = 18 + 18 + 18 = 54.

Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Сможешь найти основание? Задача про медиану равнобедренного треугольникаСкачать

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Видео:№234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.Скачать

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

📽️ Видео

Определение угла равнобедренного треугольникаСкачать

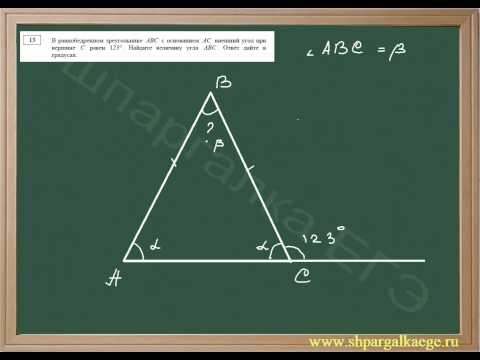
Найдите угол при вершине равнобедренного треугольника ★ Задача от Атанасяна #299Скачать

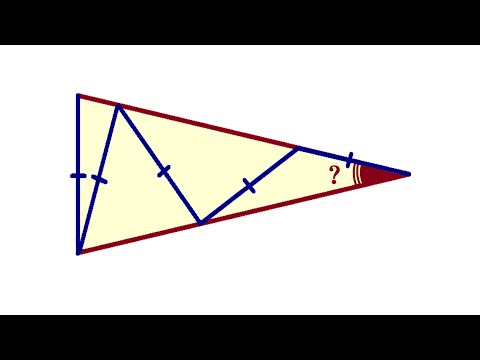
Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

№240. В равнобедренном треугольнике ABC с основанием АС биссектрисы углов А и С пересекаютсяСкачать