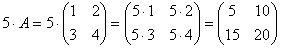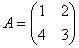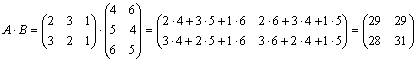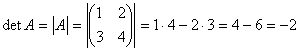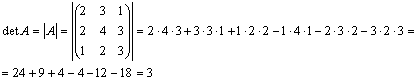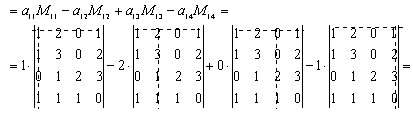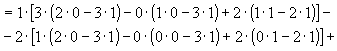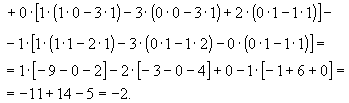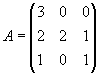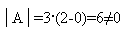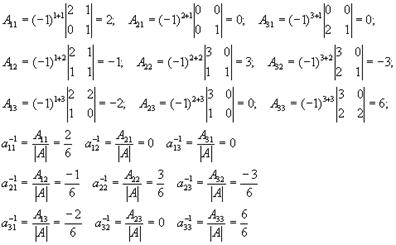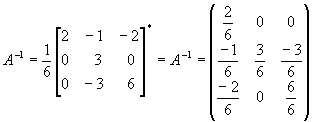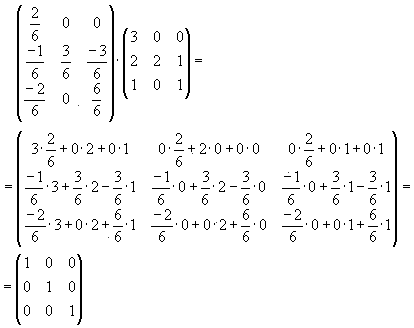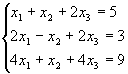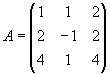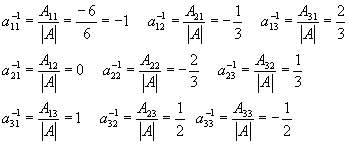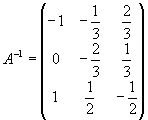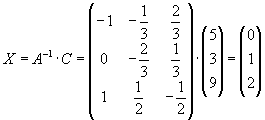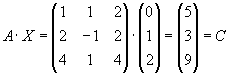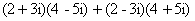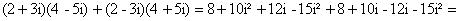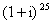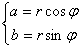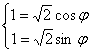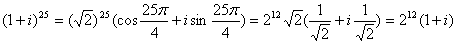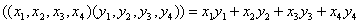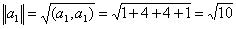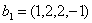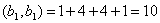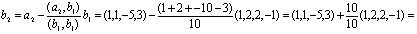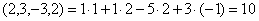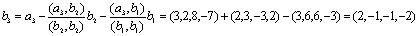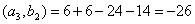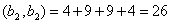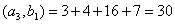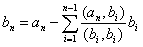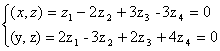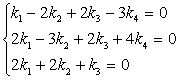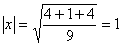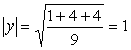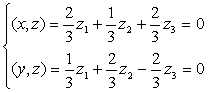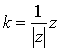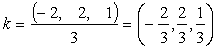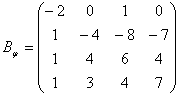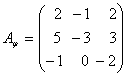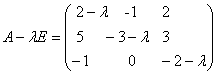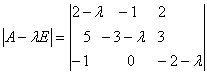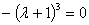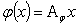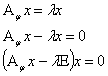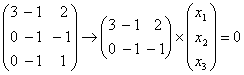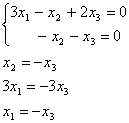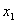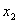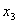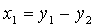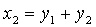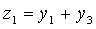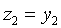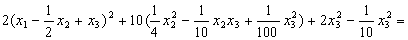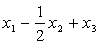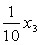Найти базис ортогонального дополнения системы векторов (5 видео)

Ортогональные дополнения евклидова пространства

Ортогональным дополнением непустого подмножества [math]M[/math] евклидова пространства [math]mathbb[/math] называется множество векторов, ортогональных каждому вектору из [math]M[/math] . Ортогональное дополнение обозначается

forall mathbfin M Bigr>.[/math]

Рассмотрим примеры ортогональных дополнений евклидова пространства.

1. Ортогональным дополнением нулевого подпространства [math] <mathbf> triangleleft mathbb[/math] служит все пространство [math]mathbb colon, <mathbf>^= mathbb[/math] . Ортогональным дополнением всего пространства является его нулевое подпространство [math]mathbb^= <mathbf>[/math] .

2. Пусть в пространстве [math][/math] радиус-векторов (с началом в точке [math]O[/math] ) за даны три взаимно перпендикулярных радиус-вектора [math]overrightarrow[/math] , [math]overrightarrow[/math] и [math]overrightarrow[/math] . Тогда ортогональным дополнением вектора [math]overrightarrow[/math] является множество радиус- векторов на плоскости, содержащей векторы [math]overrightarrow[/math] и [math]overrightarrow[/math] , точнее, [math]<overrightarrow>^= operatorname(overrightarrow,overrightarrow)[/math] . Ортогональным дополнением векторов [math]overrightarrow[/math] и [math]overrightarrow[/math] служит множество радиус-векторов на прямой, содержащей вектор [math]overrightarrowcolon <overrightarrow,overrightarrow>^= operatorname (overrightarrow)[/math] . Ортогональным дополнение трех заданных векторов служит нулевой радиус-вектор: [math]<overrightarrow, overrightarrow, overrightarrow>^= <overrightarrow>[/math] .

3. В пространстве [math]P_2(mathbb)[/math] многочленов степени не выше второй со скалярным произведением (8.29) задано подмножество [math]P_0(mathbb)[/math] — многочленов нулевой степени. Найдем ортогональное дополнение этого подмножества. Для этого приравняем нулю скалярное произведение многочлена [math]p_2(x)=ax^2+bx+c[/math] на постоянный многочлен [math]p_0(x)=dcolon[/math] [math]langle p_2(x),p_0(x)rangle= acdot0+bcdot0+ccdot d=0[/math] . Поскольку величина [math]d[/math] произвольная, то [math]c=0[/math] . Следовательно, ортогональным дополнением подмножества [math]P_0(mathbb)[/math] является множество многочленов из [math]P_0(mathbb)[/math] с нулевым свободным членом.

Содержание

Свойства ортогонального дополнения
Нахождение ортогонального дополнения подпространства
Найти базис ортогонального дополнения системы векторов
Ортогональное дополнение. Ортогональная проекция вектора на подпространство
💥 Видео

Видео:Как разложить вектор по базису - bezbotvyСкачать

Свойства ортогонального дополнения

Рассмотрим свойства ортогональных дополнений подмножеств n-мерного евклидова пространства [math]mathbb[/math] .

1. Ортогональное дополнение [math]M^[/math] непустого подмножества [math]Msubset mathbb[/math] является линейным подпространством, т.е. [math]M^ triangleleft mathbb[/math] , и справедливо включение [math]Msubset (M^)^[/math] .

В самом деле, множество [math]M^[/math] замкнуто по отношению к операциям сложения векторов и умножения вектора на число, так как сумма двух век торов, ортогональных [math]M[/math] , ортогональна [math]M[/math] , и произведение вектора, ортогонального [math]M[/math] , на любое число является вектором, ортогональным [math]M[/math] . До кажем включение [math]Msubset (M^)^[/math] . Пусть [math]mathbfin M[/math] , тогда [math]langle mathbf,mathbfrangle=0[/math] для любого вектора [math]mathbfin M^[/math] . Но это означает, что [math]mathbfsubset (M^)^[/math] .

2. Пересечение любого непустого подмножества [math]Msubset mathbb[/math] со своим ортогональным дополнением есть нулевой вектор: [math]Mcap M^= <mathbf>[/math] .

Действительно, только нулевой вектор ортогонален самому себе.

3. Если [math]L[/math] — подпространство [math]mathbb

(Ltriangleleft mathbb)[/math] , то [math]mathbb=Loplus L^[/math] .

Действительно, возьмем в [math]L[/math] ортогональный базис [math](mathbf)= (mathbf_1, ldots,mathbf_k)[/math] . До полним его векторами [math](mathbf)= (mathbf_,ldots, mathbf_n)[/math] до ортогонального базиса [math](mathbf),,(mathbf)[/math] всего пространства [math]mathbb[/math] . Тогда произвольный вектор [math]mathbfin mathbb[/math] можно представить в виде суммы

где [math]mathbfin L[/math] , а [math]mathbfin L^[/math] , так как [math]langle mathbf,mathbf_irangle= sum_^mathbflangle mathbf_j, mathbf_i rangle_<_>=0[/math] для [math]i=1,ldots,k[/math] . Следовательно, любой вектор пространства [math]mathbb[/math] раскладывается по подпространствам [math]L[/math] и [math]L^[/math] , т.е. [math]mathbb= L+L^[/math] . Эта алгебраическая сумма является прямой суммой по свойству 2, поскольку [math]Lcap L^=<mathbf>[/math] . Следовательно, [math]mathbb=Loplus L^[/math] .

4. Если [math]Ltriangleleft mathbb[/math] , то [math]dim<L^>= dimmathbb-dim[/math] .

5. Если [math]L[/math] — подпространство [math]mathbb[/math] , то [math]L=(L^)^[/math] .

Из первого свойства следует включение [math]Lsubset(L^)^[/math] . Докажем, что [math](L^)^subset L[/math] . Действительно, пусть [math]mathbfin (L^)^[/math] . По свойству 3: [math]mathbf=mathbf+mathbf[/math] , где [math]mathbfin L,

mathbfin L^[/math] . Найдем скалярное произведение

Следовательно, [math]langle mathbf,mathbfrangle=0[/math] , и согласно аксиоме 4 скалярного произведения [math]mathbf=mathbf[/math] , поэтому [math]mathbf=mathbf+ mathbf= mathbf+mathbf=mathbfin L[/math] . Значит, [math](L^)^subset L[/math] . Из двух включений [math]Lsubset (L^)^[/math] и [math](L^)^ subset L[/math] следует равенство [math]L=(L^)^[/math] .

6. Если [math]L_1triangleleft mathbb[/math] и [math]L_2triangleleft mathbb[/math] , то [math](L_1+L_2)^=L_1^cap L_2^[/math] и [math](L_1cap L_2)^= L_1^+ L_2^[/math] .

Последние свойства аналогичны свойствам алгебраических дополнений.

Видео:Ортогональное дополнение. ПримерСкачать

Нахождение ортогонального дополнения подпространства

Ранее для описания подпространств линейных пространств использовались два способа описания (внешний и внутренний). Рассмотрим применение этих способов описания для нахождения ортогональных дополнений подпространств. Учитывая изоморфизм евклидовых пространств, будем рассматривать арифметическое пространство [math]mathbb^n[/math] со скалярным произведением (8.27).

Для заданного подпространства [math]Ltriangleleft mathbb^n[/math] требуется найти его ортогональное дополнение [math]L^[/math] . В зависимости от способа описания подпространства [math]L[/math] используем одно из следующих двух утверждений.

1. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как линейная оболочка [math]L=operatorname(a_1,ldots,a_k)[/math] столбцов матрицы [math]A= begina_1&cdots&a_kend[/math] , то множество решений однородной системы [math]Ax=o[/math] является его ортогональным дополнением [math]L^triangleleft mathbb^n[/math] , т.е.

2. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как множество решений однородной системы [math]Ax=o[/math] [math]m[/math] уравнений с [math]n[/math] неизвестными, то линейная оболочка столбцов [math]a_1^T,ldots,a_m^T[/math] транспонированной матрицы [math]A^T=begina_1^T&cdots&a_m^Tend[/math] является его ортогональным дополнением [math]L^triangleleft mathbb^n[/math] , т.е.

где [math]a_i^T[/math] — i-й столбец матрицы [math]A^T[/math] .

Докажем, например, первое утверждение. Линейное однородное уравнение

1. В отличие от алгебраического дополнения [math]L^[/math] подпространстве [math]Ltriangleleft mathbb[/math] ортогональное дополнение [math]L^[/math] находится однозначно.

2. Ортогональное дополнение [math]L^[/math] подпространства [math]Ltriangleleft mathbb[/math] в силу свойства 3 является также и алгебраическим дополнением. Это обстоятельстве учитывалось при нахождении алгебраических дополнений при помощи утверждений (8.16) и (8.17), которые по существу совпадают с утверждениями (8.34) и (8.35).

Пример 8.19. В примере 8.10 для линейного подпространства [math]L= operatorname[(t-1)^2,(t+1)^3][/math] пространства [math]P_3(mathbb)[/math] многочленов не более, чем 3-й степени, было найдено алгебраическое дополнение

Доказать, что это алгебраическое дополнение является ортогональным дополнением подпространства [math]L[/math] евклидова пространства [math]P_3(mathbb)[/math] со скалярным произведением (8.29).

Решение. Для решения задачи достаточно показать, что образующие подпространства [math]L:[/math]

ортогональны образующим алгебраического дополнения [math]L^:[/math]

Видео:Ортогональное дополнение (задача 1366)Скачать

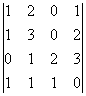
Найти базис ортогонального дополнения системы векторов

Задачи по алгебре. Выпуск 2.

Задача 1. Найти 5А, если

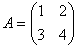
Задача 2. Найти А +В, если

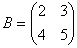
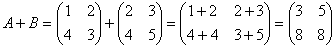
Задача 3. Найти АВ , если

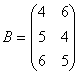
Задача 4. Найти транспонированную матрицу относительно матрицы

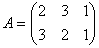
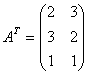
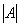
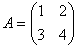
Задача 5. Найти , если

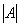
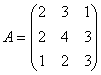
Задача 6. Найти , если

Задача 7. Вычислить определитель

Решение: Разложим определитель по первой строке:

Задача 8. Найти обратную матрицу для матрицы

Определитель нулю не равен, следовательно, обратная матрица существует. Найдем алгебраические дополнения (знаки их учтем сразу), т. е.

Мы сами можем проверить результат, Известно, что 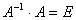. Так ли это?

Получилась единичная матрица. Значит, обратная матрица найдена верно.

Задача 9. Решить систему матричным способом:

Не является ли матрица А вырожденной? Найдем ее определитель: det А =1•[-1•4 – 1•2] – 1•[2•4 – 2•4] + 2•[2•1 – 4•(-1)] = -6 + 12 = 6

Определитель не равен нулю, то есть матрица не вырожденная. Значит, существует обратная матрица

Можно убедиться проверкой в правильности решения: подставим вектор Х в первоначальное матричное уравнение.

Действительно вектор Х удовлетворяет заданной системе.

Задача 10. Решить систему с помощью формул Крамера :

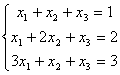
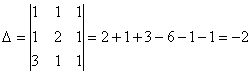
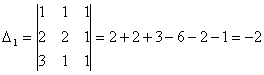
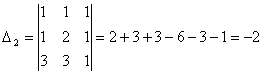
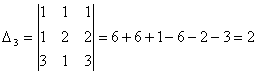
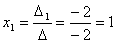
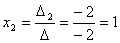
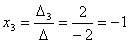
Задача 11. Вычислить :

Раскроем скобки и получим:

Так как 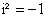, то получаем:

Задача 12. Вычислить, пользуясь формулой Муавра:

Представим число z в тригонометрической форме.

, следовательно, а=1, b =1 и .

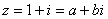
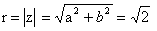
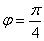
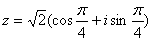
Применим формулу Муавра:

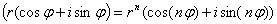
Задача 13. Выполнить деление с остатком f ( x )= x 3 — x 2 — x на x -1+2 i .

Решение: Составим таблицу, в которой над чертой расположены коэффициенты многочлена f ( x ), под чертой соответствующие коэффициенты частного и остаток, последовательно вычисляемые, а слева сбоку – значение c = 1-2 i в данном примере.

Таким образом: f ( x )= x 3 — x 2 — x =( x -1+2 i ) ( x 2 -2 ix -5-2 i )-9+8 i .

Ответ : f(x)=x 3 -x 2 -x=(x-1+2i) (x 2 -2ix-5-2i)-9+8i.

Задача 14. Применяя процесс ортогонализации, построить ортогональный базис подпространства, натянутого на данную систему векторов.

, ,

;

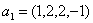
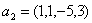
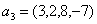
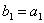
Задача 15. Проверить, что векторы х = (1, -2, 2, -3), у = (2, -3, 2, 4) ортогональны, и дополнить их до ортогональных базисов.

Решение: Найдем скалярное произведение данных векторов: ( х , у) = 2+6+4-12 = 0 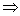х , у – ортогональны .

Найдем векторы, дополняющие данную систему векторов до ортогонального базиса.

Пусть z = (z₁, z₂, z ₃, z ₄) попарно ортогонален с данными векторами, т.е. ( x , z ) = 0 и ( y , z ) = 0. Получаем следующую систему:

Эта система имеет множество решений, например,

Пусть теперь k = ( k ₁, k ₂, k ₃, k ₄) попарно ортогонален с векторами x , y , z . Получаем следующую систему:

Эта система имеет множество решений, например,

Таким образом, можно добавить векторы

(2, 2, 1, 0), (-5, 2, 6, 1).

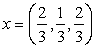
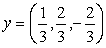
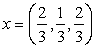
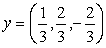
Задача 16. Найти векторы, дополняющие следующую систему векторов и до ортонормированного базиса.

Пусть z = (z₁, z₂, z ₃) попарно ортогонален с данными векторами, т.е. ( x , z ) = 0 и ( y , z ) = 0. Получаем следующую систему:

Эта система имеет множество решений, например,

Нормируя этот вектор, получим вектор, дополняющий данную систему векторов до ортонормированного базиса:

Задача 17. Доказать, что проектирование трехмерного пространства на координатную плоскость натянутую на вектора e ₁, e ₂ параллельно оси координат вектора e ₃, является линейным преобразованием, и найти его матрицу в базисе e ₁, e ₂, e _3..

Решение: Пусть L — трёхмерное пространство, e ₁, e ₂, e ₃ — базис L , преобразование 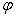— проектирование L на координатную плоскость векторов e ₁, e ₂ параллельно оси координат вектора e ₃.

Пусть х — произвольный вектор L , т.е. x Î L .

Пусть x =( x ₁, x ₂, x ₃) — координаты вектора x в базисе e ₁, e ₂, e ₃, т.е. x = x ₁ e ₁+ x ₂ e ₂+ x ₃ e ₃. Тогда при преобразовании j имеем:

Докажем, что для любых x Î L , y Î L и числа l

1) j ( x+y )= j (x)+ j (y),

2) j ( l x )= l j (x).

j ( l x ) = ( l x ₁, l x ₂, 0) = l ( x ₁, x ₂, 0) = l j ( x ) .

Следовательно, j — линейное преобразование.

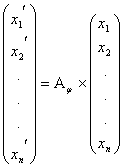
Найдем матрицу преобразования j в базисе e ₁, e ₂, e ₃. Известно, что координаты образа j ( x ) вектора x при линейном преобразовании выражаются через координаты вектора x в том же базисе при помощи матрицы преобразования A _j следующим образом:

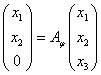
Откуда следует, что

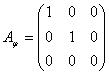
Задача 18. Линейное преобразование φ в базисе е ₁ , е₂, е₃, е₄ имеет матрицу

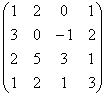
Выпишем матрицу перехода от базиса е ₁ ,е₂,е₃,е₄ к новому базису:

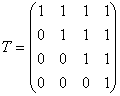
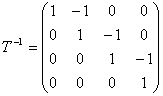
Теперь найдем матрицу преобразования В _j в новом базисе по формуле В _j =Т -1 А _j Т.

Задача 19. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:

Решение: Собственные значения являются корнями характеристического уравнения преобразования j .

Составим характеристическую матрицу:

Найдем определитель матрицы и вычислим корни характеристического уравнения:

= (2 — )(3+ )(2+ )+3-2(3+ )-5(2+ ) =

= +3-6-2 -10-5 =

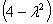
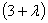
= 12+4 -3 -7 -13 = ,

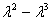
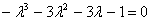
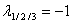
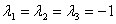
Получим собственные значения: или .

Для каждого собственного значения найдем собственный вектор.

По определению имеем: .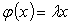

Но, в тоже время,

Беря значением = -1, получаем с.л.а .у . :

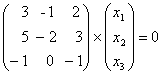
Собственными векторами будут являться вектора, входящие в фундаментальную систему решений (ф.с.р.) этой с.л.а .у . Найдем ф.с.р. это с.л.а .у .

Таким образом, собственным вектором, отвечающим собственному значению = -1, является вектор .

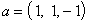
Задача 20. Найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду, для следующей квадратичной формы: .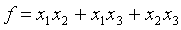

Решение: Ввиду отсутствия в этой форме квадратов неизвестных мы выполним сначала невырожденное линейное преобразование:

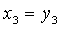
после чего получим .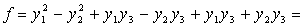

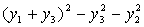
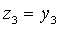
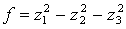
, получим, что .

Найдем невырожденное линейное преобразование.

, , .

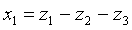
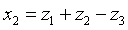
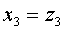
Задача 21. Следующую квадратичную форму привести к каноническому виду с целыми коэффициентами посредством невырожденного линейного преобразования с рациональными коэффициентами и найти выражение новых неизвестных через старые.

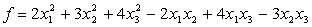
Решение: Приведем данную форму к каноническому виду:

= =2 =

= .

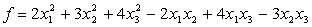
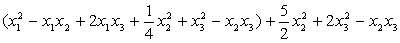
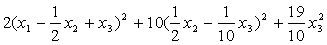
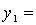
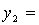
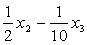
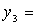
получим канонический вид квадратичной формы:

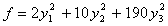
Видео:Образуют ли данные векторы базисСкачать

Ортогональное дополнение. Ортогональная проекция вектора на подпространство

Пусть Е — евклидово пространство, а L — его подпространство. Множество L 1 — векторов в Е, ортогональных к каждому вектору подпространства L, называют ортогональным дополнением к подпространству L.

Теорема 8.6. Ортогональное дополнение IA к подпространству L евклидова пространства Е является подпространством в Е.

> Пусть уi,y2 € ZA. Тогда для любого вектора х ? L имеем: (ж, г/1) = 0 и (х,у2) = 0. Следовательно,

т.е. вектор у + у2 ортогонален любому вектору х € L. Это означает, что У1+У2 € ZA. Мы доказали, что сумма любых двух векторов множества ZA принадлежит ZA. Аналогично для любого действительного числа Л и любого х € L имеем:

т.е. вектор Л у ортогонален любому вектору х е L, а значит, принадлежит ZA. Таким образом, множество ZA замкнуто относительно сложения векторов и умножения векторов на числа и, следовательно, является подпространством. ?

Теорема 8.7. Конечномерное евклидово пространство Е является прямой суммой любого своего подпространства L и его ортогонального дополнения ZA, т.е. ортогональное дополнение к подпространству является его прямым дополнением.

> Пусть в пространстве L выбран ортогональный базис, состоящий из векторов ai, 02, . а&. Дополним его до ортогонального базиса пространства Е векторами fk+i, fk+2, •••, fn и по построенному базису

разложим произвольный вектор х из Е. Тогда получим где положено

Вектор у принадлежит подпространству Z, поскольку он является линейной комбинацией векторов базиса в L. Покажем, что вектор z принадлежит ортогональному дополнению LА Для этого замечаем, что по построению векторы fk+i, fk+2, fn ортогональны базисным

векторам ai, Это очевидное следствие теоремы о размерности суммы подпространств (см. теорему 4.23). ?

Следствие 8.3. Ортогональным дополнением к подпространству ZA является подпространство L.

> Так как каждый вектор из L ортогонален каждому вектору из ZA, то подпространство L содержится в (ZA)A Кроме того, выполняются соотношения Е = L 0 ZA, Е = (L— L )- L ф ZA, и по предыдущему следствию подпространства L и (ZA) 1 — имеют одинаковую размерность. Поэтому эти подпространства совпадают. ?

Следствие 8.4. Если L — подпространство в евклидовом пространстве Е, то любой вектор х € Е имеет разложение

где хо G L, х 1 — G /А. Такое разложение единственно.

> Это утверждение — фактически расшифровка утверждения, что Е = L Ф ZA. ?

Пример 8.9. В четырехмерном пространстве Е± скалярное произведение в заданном базисе определено формулой (8.5). Построить ортогональное дополнение ZA для подпространства L = (а^аг), где a, = (1,1,1, l) r , а₂ = (1, -1,1,1) т .

Решение. Векторы а и а2 составляют базис в L. Дополним эту систему до базиса в Е± векторами Ъ и 62, удовлетворяющими условиям

и положим L = (61,62)- Векторы 61, 62 являются решениями системы из двух уравнений (ai,x) = 0, (а,2,х) = 0, и в качестве их можно взять любую фундаментальную систему решений, например, 61 = (—1,0,1,0) т , 62 = (—1,0,0,1) т . Из выбора векторов 61 и 62 следует, что они составляют базис в L L , т.е. L = L L . ?

Пусть L — подпространство евклидова пространства Е. Каждый вектор у ? Е может быть единственным способом представлен в виде

где уо ? L, а вектор у 1 — ортогонален к каждому вектору из L, т.е. у 1 — ? L х . Вектор уо называют ортогональной проекцией вектора у на пространство L и обозначают прьУ, а вектор y L называют ортогональной составляющей вектора у. Очевидно, что если у ? L, то прьу = у, и, наоборот, если прьу = : Действительно, пусть у — произвольный вектор, опущенный из конца вектора х на подпространство L и х 1 — — ортогональная составляющая вектора х, т.е. перпендикуляр, опущенный из конца вектора х на подпространство L. Тогда

поскольку концы векторов у их 1 лежат в L. Поэтому

так как векторы у — х 1 — их 1 ортогональны. ?

Доказанные утверждения является естественным обобщением известного из элементарной геометрии утверждения о том, что перпендикуляр короче любой наклонной, опущенной из той же точки на плоскость.

Длину ортогональной составляющей х 1 — вектора х принимают за кратчайшее расстояние от вектора х до подпространства L.

Ортогональная проекция вектора у на подпространство L является частным случаем проекции вектора на подпространство параллельно подпространству L₂, являющемуся прямым дополнением к L (см. разд. 4.11). В случае ортогональной проекции Ь₂ = Ь 1 .

На практике при отыскании ортогональной проекции вектора х на подпространство L = (ai, а₂, •••?> &fc) поступают следующим образом. В разложении

вектора х на ортогональную проекцию жо = np_LT и ортогональную составляющую х 1 — вектор Xq можно представить в виде линейной комбинации

Тогда равенство х = Хо + х 1 принимает вид:

Для отыскания коэффициентов oi, 02, . о& умножим равенство (8.16) скалярно на векторы а, а₂, . ак- Учитывая, что (а^аг 1- ) = = (а₂,х ± ) = . = (ак,х?*?) = 0, получаем систему линейных уравнений

относительно неизвестных оц, а₂, . а к. Из этой системы находят коэффициенты oi, а₂, . о^. В матричной форме равенство (8.15) и система (8.17) записываются в виде

где А = (oi, а₂. а*,) — матрица, для которой столбцами являются столбцы координат векторов а, а₂, . а&; о — (01,02, . о*;) т — столбец высоты к. Использование системы (8.17), или, что тоже самое системы (8.19), указывает на то (см. п.8.21), что отыскание коэффициентов ai, а₂, . ак для равенства (8.15) равносильно решению методом наименьших квадратов системы А о = х с неизвестным столбцом

Если система векторов oi, 2, • ••, ftfc линейно независимая, то в равенстве (8.19) матрица А т А невырожденная, так как она представляет собой матрицу Грама этой системы векторов (см. теорему 8.1). В этом случае из уравнения (8.19) однозначно определяется столбец а:

Учитывая равенство (8.18), заключаем, что

Пример 8.10. Для вектора х = (3,6,0) т найти ортогональную проекцию Xq на подпространство L = (а^аг) и ортогональную составляющую т х , если ay = (1, —1,0) т , т .

Решение. Запишем xq = np_L.x в виде хд = ау ау + Коэффициенты ау и «2 можно найти, решив систему (8.17), которая в данном случае имеет вид:

Вычислим все скалярные произведения. В результате получим

Решая систему относительно неизвестных од иаг, находим, что од = = су2 = 3. Таким образом, пр/,т = Зау + Заг = (0,3,3) т и х^ = = х — np_LT = (3,3, —3) т .

Поскольку векторы а у, а2 линейно независимые, то можно также воспользоваться формулой (8.20). Вычислив

Заметим, что если е = (ei, е₂,е_п) — ортоиормированный базис в евклидовом пространстве Е, а подпространство L является линейной оболочкой части базисных векторов, например, L = (ei, е₂. е*,), то для любого вектора

ортогональная проекция прь-т совпадает с суммой слагаемых в разложении х по базису, соответствующих векторам, порождающим L. а ортогональная проекция — с суммой всех остальных слагаемых, т.е.

Например, для вектора х = (1,2, 3,4,5) т проекция на подпространство L = (б1,е2,ез) равна Xq = (1,2,3,0,0) т , и его ортогональная составляющая х 1 — = (0,0,0,4, 5) т . ?