С задачками по геометрии сталкиваются все в средней школе. Кому-то такие задачки даются сложно, а кто-то их щелкает, как орешки. На самом деле эти задачи не особо сложные, просто нужно вникнуть и понять определенный алгоритм решения. Давайте подробнее разберем, как найти катет прямоугольного треугольника.
- Геометрические определения
- Свойства сторон в прямоугольном треугольнике
- Формулы для решения задач
- Примеры решения задач
- Задача №1:
- Задача №2:
- Найти ас в прямоугольном треугольнике
- Прямоугольный треугольник. Теорема Пифагора.
- теория по математике 📈 планиметрия
- Свойства прямоугольного треугольника
- Признаки равенства прямоугольных треугольников
- Теорема Пифагора
- Египетский треугольник
- Пифагоровы тройки
- 📹 Видео
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Геометрические определения
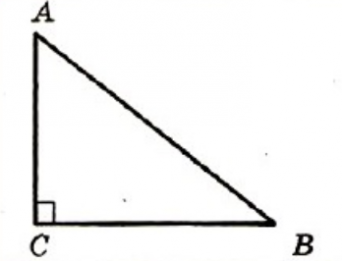
- Если у треугольника есть прямой угол (∠=90 о ), то он является прямоугольным.
- Катет – линия, создающая угол 90 градусов в треугольнике.
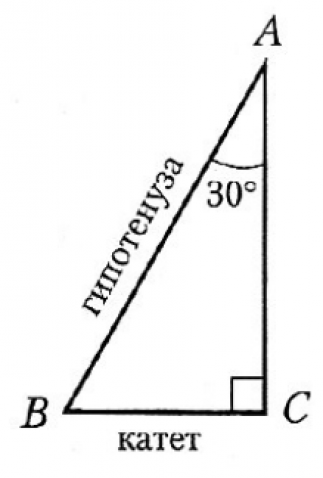
- Гипотенуза – линия, которая находится напротив угла равного 90 градусов.
- Две ортогональные линии образуют прямой угол, величина которого 90 градусов. Еще можно сказать, что это половина развернутого угла.
Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Свойства сторон в прямоугольном треугольнике
Гипотенуза всегда больше каждого из катетов.
Сторона, которая находится напротив угла равного 30 градусов, равна половине величины гипотенузы.
К прямоугольному треугольнику можно применить теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Видео:Высота прямоугольного треугольникаСкачать

Формулы для решения задач
- Если мы знаем величину одного катета А и гипотенузы С, то второй катет B мы вычислим при помощи теоремы Пифагора.
- Угол А мы может определись с помощью формулы синуса:
- Так как сумма всех углов геометрической фигуры всегда равна 180 градусов, то другой острый угол можно вычислить по формуле:
Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Примеры решения задач
Задача №1:
В треугольнике АВС с ∠А=90 градусов, ∠С=60 градусов и катетом АВ=5 см. Найти длину катета АС.
В прямоугольном треугольнике АВС найдем угол В:
∠В=90 о — ∠С=90 о — 60 о = 30 о
Поскольку ∠В=30 о , то катет АВ равен половине гипотенузы ВС, а значит,
Длину катета АС найдем с помощью теоремы Пифагора:
Задача №2:
В равнобедренном и прямоугольном треугольнике АВС гипотенуза больше катета на 2 см. Найти длину сторон треугольника.
В треугольной фигуре АВС обозначим катеты АВ=АС=х, тогда ВС=2+х. Запишем теорему Пифагора для данного треугольника:
ВС 2 = АВ 2 + АС 2 => (х+2) 2 = х 2 + х 2 или х 2 – 4х – 4 = 0
Решая это уравнение и учитывая условия задачи, получим
т.е. АВ = АС = (2+2) см, ВС = (4+2) см
Ответ: АВ = АС = (2+2) см, ВС = (4+2) см
Как видите, процесс решения геометрических задач по нахождению катета в прямоугольном треугольнике не особо сложный. Нужно просто приложить усилия, посидеть и вникнуть в суть задачи. Когда начнете писать формулы, решение придет к вам само. Удачи в решении задачек по геометрии, теперь вы знаете, как найти катет прямоугольного треугольника.
Видео:Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Найти ас в прямоугольном треугольнике
Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах.
Сумма острых углов прямоугольного треугольника равна 90°. Острые углы прямоугольного треугольника относятся как 4 части к 5 частям, сумма этих углов 4 + 5 = 9 частей. Поэтому одна часть равна 10°. Так как больший угол содержит в себе 5 частей, он равен 5·10° = 50°.
В треугольнике ABC угол C равен 90°, Найдите AB.
Так как треугольник ABC — прямоугольный, то . Имеем:
В треугольнике ABC угол C равен 90°, . Найдите AB.
Так как треугольник ABC — прямоугольный, то . Имеем:
Аналоги к заданию № 311387: 311399 311498 311500 Все
Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведенную к гипотенузе.
Пусть катеты имеют длины a и b, а гипотенуза — длину Пусть длина высоты, проведённой к гипотенузе равна
Найдём длину гипотенузы по теореме Пифагора:
Площадь прямоугольного треугольника может быть найдена как половина произведения катетов или как половина произведения высоты, проведённой к гипотенузе на гипотенузу:
Видео:Нахождение стороны прямоугольного треугольникаСкачать

Прямоугольный треугольник. Теорема Пифагора.
теория по математике 📈 планиметрия
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.
Видео:Теорема Пифагора для чайников)))Скачать

Свойства прямоугольного треугольника
- В прямоугольном треугольнике гипотенуза является наибольшей стороной.
- В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .
Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .
- Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
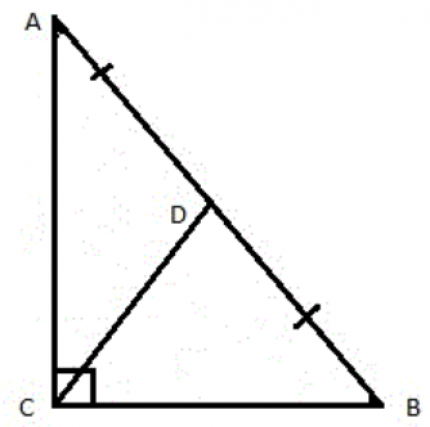
- Медиана, проведенная к гипотенузе, равна её половине.
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.
Видео:КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Признаки равенства прямоугольных треугольников
Существует 4 признака равенства прямоугольных треугольников:
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:
- по катетам;
- по катету и прилежащему острому углу;
- по гипотенузе и острому углу;
- по гипотенузе и катету.
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Теорема Пифагора
Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».
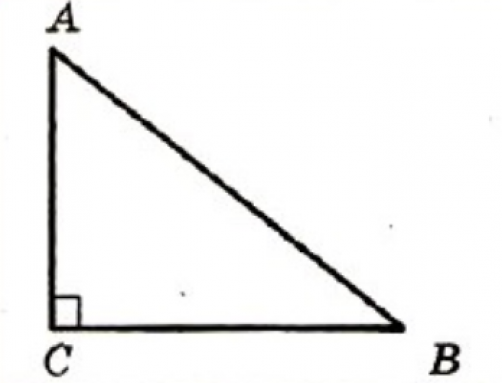
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2
Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.
Египетский треугольник
Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.
Пифагоровы тройки
Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.
📹 Видео
7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

№172. Катет АС прямоугольного треугольника ABC с прямым углом С лежит в плоскости α, а уголСкачать

Лайфхак нахождения катета в прямоугольном треугольникеСкачать
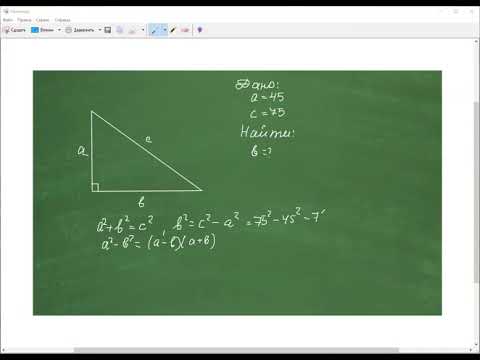
ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

Определение длины гипотенузыСкачать

Геометрия из № 23 ОГЭ В прямоугольном треугольнике ABC с прямым углом С известны катеты: АС = 6Скачать

Что с углами. Прямоугольный треугольник #shortsСкачать

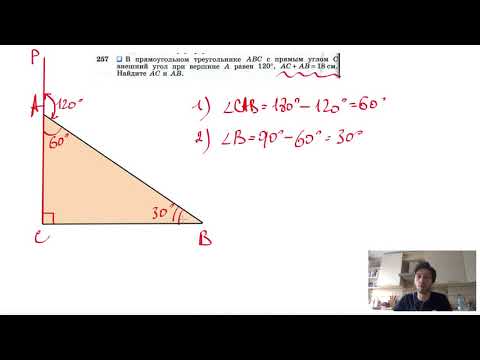
№257. В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120°Скачать
Свойство медианы в прямоугольном треугольнике #shortsСкачать
Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать