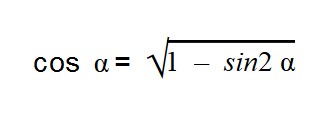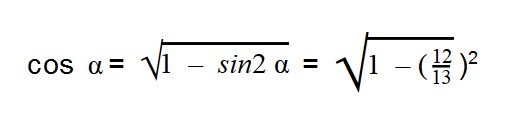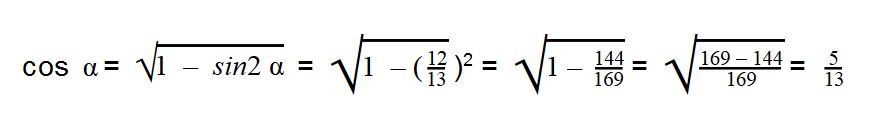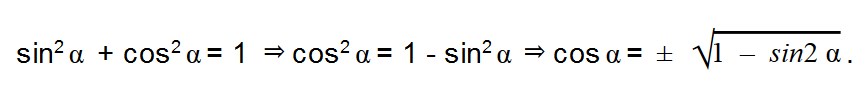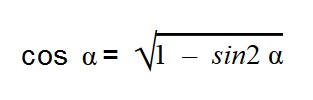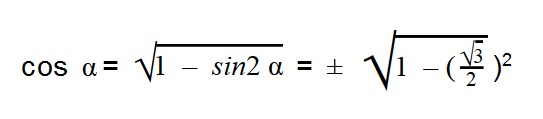- Тождество – равенство, верное при любых значениях переменных, кроме тех при которых какая-либо часть тождества не имеет смысла.
- Как доказывать тождество?
- Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».
- Как доказать основное тригонометрическое тождество
- Ответы на часто задаваемые вопросы:
- Основное тригонометрическое тождество
- Связь между sin и cos одного угла
- Тангенс и котангенс через синус и косинус
- Связь между тангенсом и котангенсом
- Тангенс и косинус, котангенс и синус
- Примеры решения задач
- Основные тригонометрические тождества: их формулировки и вывод
- Связь между sin и cos одного угла
- Тангенс и котангенс через синус и косинус
- Связь между тангенсом и котангенсом
- Тангенс и косинус, котангенс и синус
- 📸 Видео
Тождество – равенство, верное при любых значениях переменных, кроме тех при которых какая-либо часть тождества не имеет смысла.
А вот выражение (frac=x) является тождеством только при условии (x≠0) (иначе левая часть не существует).
Видео:Основное тригонометрическое тождествоСкачать

Как доказывать тождество?
Рецепт до одури прост:
Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».
Для того, чтоб это сделать можно:
- Преобразовывать только правую или только левую часть.
- Преобразовывать обе части одновременно.
- Использовать любые допустимые математические преобразования (например, приводить подобные; раскрывать скобки; переносить слагаемые из одной части в другую, меняя знак; умножать или делить левую и правую часть на одно и то же число или выражение, не равное нулю и т.д.).
- Использовать любые математические формулы.
Именно четвертый пункт при доказательстве тождеств используется чаще всего, поэтому все формулы тригонометрии нужно знать, помнить и уметь использовать.
Пример. Доказать тригонометрическое тождество (sin2x=2sinxcdot cos)
Решение:
(sin2x=2 sinxcdot cos )
Будем преобразовывать левую часть.
Представим (2x) как (x+x)…
Левая часть равна правой – тождество доказано.
Будем преобразовывать только левую часть. Приведем слагаемые к общему знаменателю.
Применим в числителе вездесущие основное тригонометрическое тождество: (sin^2+cos^2=1).
Левая часть равна правой, тождество доказано.
Здесь будем преобразовывать только правую часть, стремясь свести ее к левой. Левую же оставляем неизменной. Вспоминаем формулу двойного угла для косинуса .
Теперь сделаем почленное деление в дроби (т.е. применим правило для сложения дробей в обратную сторону): (frac) (=) (frac) (+) (frac)
Первую дробь правой части сократим, а ко второй применим свойство степени : (frac) (=) ((frac)^n) .
Ну, а синус деленный на косинус равен тангенсу того же угла:
Левая часть равна правой, тождество доказано.
Здесь будем преобразовывать обе части:
— в левой: преобразуем (cos2t) по формуле двойного угла;
— а в правой (ctg(π+t)) по формуле приведения .
Теперь работаем только с левой частью.
В числителе воспользуемся формулой сокращенного умножения , в знаменателе вынесем за скобку синус.
Сократим дробь на (cos+sin).
Почленно разделим дробь, превратив ее в две отдельные дроби.
Первая дробь это котангенс , а вторая равна единице.
Левая часть равна правой, тождество доказано.
Как видите, все довольно несложно, но надо знать все формулы и свойства.
Видео:Основное тригонометрическое тождество. 9 класс.Скачать
Как доказать основное тригонометрическое тождество
Два простых способа вывести формулу (sin^2x+cos^2x=1). Нужно знать только теорему Пифагора и определение синуса и косинуса.
Видео:Доказательство основного тригонометрического тождества (видео 1)|Тригонометрия | МатематикаСкачать

Ответы на часто задаваемые вопросы:
Вопрос: Как определить, что в тождестве надо преобразовывать – левую часть, правую или обе вместе?
Ответ: Нет никакой разницы – в любом случае вы получите один и тот же результат. Например, в третьем примере мы легко могли бы получить из левой части (1-tg^2 t) правую (frac) (попробуйте сделать это сами). Или преобразовывать обе, с тем чтоб они «встретились посередине», где-то в районе (frac) (=) (frac) . Поэтому вы можете доказывать любым удобным вам способом. Какую «тропинку» видите – по той и идите. Главное только – преобразовывайте «законно», то есть понимайте на основании какого свойства, правила или формулы вы делаете очередное преобразование.
Видео:Основное тригонометрическое тождество. 8 класс.Скачать

Основное тригонометрическое тождество
О чем эта статья:
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Основное тригонометрическое тождество. Тригонометрическая окружность.Скачать

Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Это значит, что точка A1 получает координаты cos α, sin α.
Образовался прямоугольный треугольник OA1B.
|OB| = |x|.
Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B| 2 + |OB| 2 = |OA1| 2 .
Записываем в виде: |y| 2 + |x| 2 = 1 2 .
Это значит, что y 2 + x 2 = 1.
sin угла α = y
cos угла α = x
Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Видео:ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА 10 класс тригонометрияСкачать

Тангенс и котангенс через синус и косинус
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
- tg α =
=
- ctg α =
=
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
ctg α = x/y
 и
и  ,
, получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Видео:Почему основное тригонометрическое тождество таково?Скачать

Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg 2 α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg 2 α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
- Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
- В результате деления получаем формулу tg 2 α + 1 =
- Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
1 + ctg 2 α =.
- Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 =
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg 2 α =
применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Видео:Доказательство основного тригонометрического тождестваСкачать

Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:
Вычисляем:
Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
Таким же образом, используя формулу, вычисляем значение котангенса:
Задачка 2. Найдите значение cos α,
если:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:

Подставляем значения sin α:
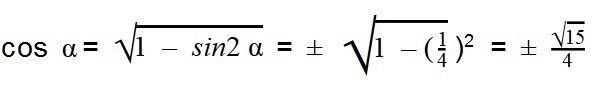
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Видео:Формулы приведения - как их легко выучить!Скачать

Основные тригонометрические тождества: их формулировки и вывод
В статье подробно рассказывается об основных тригонометрических тождествах. Эти равенства устанавливают связь между sin , cos , t g , c t g заданного угла. При известной одной функции можно через нее найти другую.
Тригонометрические тождества для рассмотрения в денной статье. Ниже покажем пример их выведения с объяснением.
sin 2 α + cos 2 α = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α
Видео:Алгебра 10 класс Тригонометрические тождества Базовый уровеньСкачать

Связь между sin и cos одного угла
Поговорим о важном тригонометрическом тождестве, которое считается основой основ в тригонометрии.
sin 2 α + cos 2 α = 1
Заданные равенства t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α выводят из основного путем деления обеих частей на sin 2 α и cos 2 α . После чего получаем t g α = sin α cos α , c t g α = cos α sin α и t g α · c t g α = 1 — это следствие определений синуса, косинуса, тангенса и котангенса.
Равенство sin 2 α + cos 2 α = 1 является основным тригонометрическим тождеством. Для его доказательства необходимо обратиться к теме с единичной окружностью .
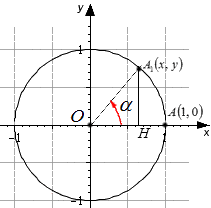
Пусть даны координаты точки А ( 1 , 0 ) , которая после поворота на угол α становится в точку А 1 . По определению sin и cos точка А 1 получит координаты ( cos α , sin α ) . Так как А 1 находится в пределах единичной окружности, значит, координаты должны удовлетворят условию x 2 + y 2 = 1 этой окружности. Выражение cos 2 α + sin 2 α = 1 должно быть справедливым. Для этого необходимо доказать основное тригонометрическое тождество для всех углов поворота α .
В тригонометрии выражение sin 2 α + cos 2 α = 1 применяют как теорему Пифагора в тригонометрии. Для этого рассмотрим подробное доказательство.
Используя единичную окружность, поворачиваем точку А с координатами ( 1 , 0 ) вокруг центральной точки О на угол α . После поворота точка меняет координаты и становится равной А 1 ( х , у ) . Опускаем перпендикулярную прямую А 1 Н на О х из точки А 1 .
На рисунке отлично видно, что образовался прямоугольный треугольник О А 1 Н . По модулю катеты О А 1 Н и О Н равные, запись примет такой вид: | А 1 H | = | у | , | О Н | = | х | . Гипотенуза О А 1 имеет значение равное радиусу единичной окружности, | О А 1 | = 1 . Используя данное выражение, можем записать равенство по теореме Пифагора: | А 1 Н | 2 + | О Н | 2 = | О А 1 | 2 . Это равенство запишем как | y | 2 + | x | 2 = 1 2 , что означает y 2 + x 2 = 1 .
Используя определение sin α = y и cos α = x , подставим данные угла вместо координат точек и перейдем к неравенству sin 2 α + cos 2 α = 1 .
Основная связь между sin и cos угла возможна через данное тригонометрическое тождество. Таким образом, можно считать sin угла с известным cos и наоборот. Чтобы выполнить это, необходимо разрешать sin 2 α + cos 2 = 1 относительно sin и cos , тогда получим выражения вида sin α = ± 1 — cos 2 α и cos α = ± 1 — sin 2 α соответственно. Величина угла α определяет знак перед корнем выражения. Для подробного выяснения необходимо прочитать раздел вычисление синуса, косинуса, тангенса и котангенса с использованием тригонометрических формул.
Чаще всего основную формулу применяют для преобразований или упрощений тригонометрических выражений. Имеется возможность заменять сумму квадратов синуса и косинуса на 1 . Подстановка тождества может быть как в прямом, так и обратном порядке: единицу заменяют на выражение суммы квадратов синуса и косинуса.
Видео:[понять нельзя заучивать] Доказательство основного тригонометрического тождестваСкачать
![[понять нельзя заучивать] Доказательство основного тригонометрического тождества](https://i.ytimg.com/vi/qpaWYfOGZx8/0.jpg)
Тангенс и котангенс через синус и косинус
Из определения косинуса и синуса, тангенса и котангенса видно, что они взаимосвязаны друг с другом, что позволяет отдельно преобразовывать необходимые величины.
t g α = sin α cos α c t g α = cos α sin α
Из определения синус является ординатой у , а косинус – абсциссой x . Тангенс – это и есть отношения ординаты и абсциссы. Таким образом имеем:
t g α = y x = sin α cos α , а выражение котангенса имеет обратное значение, то есть
c t g α = x y = cos α sin α .
Отсюда следует, что полученные тождества t g α = sin α cos α и c t g α = cos α sin α задаются с помощью sin и cos углов. Тангенс считаются отношением синуса к косинусу угла между ними, а котангенс наоборот.
Отметим, что t g α = sin α cos α и c t g α = cos α sin α верны для любого значение угла α , значения которого входят в диапазон. Из формулы t g α = sin α cos α значение угла α отлично от π 2 + π · z , а c t g α = cos α sin α принимает значение угла α , отличные от π · z , z принимает значение любого целого числа.
Видео:Тригонометрические тождества. Видеоурок 22. Алгебра 10 классСкачать

Связь между тангенсом и котангенсом
Имеется формула, которая показывает связь между углами через тангенс и котангенс. Данное тригонометрическое тождество является важным в тригонометрии и обозначается как t g α · c t g α = 1 . Оно имеет смысл при α с любым значением, кроме π 2 · z , иначе функции будут не определены.
Формула t g α · c t g α = 1 имеет свои особенности в доказательстве. Из определения мы имеем, что t g α = y x и c t g α = x y , отсюда получаем t g α · c t g α = y x · x y = 1 . Преобразовав выражение и подставив t g α = sin α cos α и c t g α = cos α sin α , получим t g α · c t g α = sin α cos α · cos α sin α = 1 .
Тогда выражение тангенса и котангенса имеет смысл того, когда в итоге получаем взаимно обратные числа.
Видео:9 класс, 10 урок, Основное тригонометрическое торжество. Формула приведенияСкачать

Тангенс и косинус, котангенс и синус
Преобразовав основные тождества, приходим к выводу, что тангенс связан через косинус, а котангенс через синус. Это видно по формулам t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α .
Определение звучит так: сумма квадрата тангенса угла и 1 приравнивается к дроби , где в числителе имеем 1 , а в знаменателе квадрат косинуса данного угла, а сумма квадрата котангенса угла наоборот. Благодаря тригонометрическому тождеству sin 2 α + cos 2 α = 1 , можно разделить соответствующие стороны на cos 2 α и получить t g 2 α + 1 = 1 cos 2 α , где значение cos 2 α не должно равняться нулю. При делении на sin 2 α получим тождество 1 + c t g 2 α = 1 sin 2 α , где значение sin 2 α не должно равняться нулю.
Из приведенных выражений получили, что тождество t g 2 α + 1 = 1 cos 2 α верно при всех значениях угла α , не принадлежащих π 2 + π · z , а 1 + c t g 2 α = 1 sin 2 α при значениях α , не принадлежащих промежутку π · z .
📸 Видео
Основное тригонометрическое тождество. Урок геометрии 9 класс.Скачать

Геометрия 9 класс (Урок№13 - Основное тригонометрическое тождество. Формулы приведения.)Скачать

Как использовать основное тригонометрическое тождество для решения сложных задач?Скачать

98. Основное тригонометрическое тождество . Формулы приведенияСкачать

Доказательства тригонометрических тождествСкачать

Основное тригонометрическое тождество. Практическая часть. 9 класс.Скачать





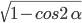
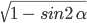
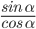
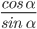
 =
= 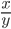 =
= 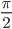 + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.