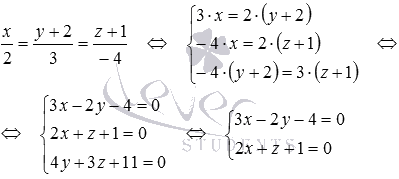За незнание этой простейшей задачи сурово наказывает Соловей-Разбойник.
Задача 75
Прямая задана уравнением 

Решение: обозначим неизвестную прямую буквой 


Вытаскиваем направляющий вектор из уравнения 
Уравнение искомой прямой 


Ответ:
Геометрия задачи выглядит незатейливо: 
Аналитическая же проверка состоит в следующих шагах:
1) Проверяем, что у прямых 

– параллельность прямых понятна без всякого чертежа!
2) Проверяем, удовлетворяет ли точка 

Примеры для самостоятельного решения сегодня будут творческими. Потому что вам ещё придётся тягаться с Бабой-Ягой, а она, знаете, любительница всяких загадок.
Задача 76
Составить уравнение прямой, проходящей через точку 

Существует рациональный и не очень рациональный способ решения. Самый короткий путь в конце книги.
С параллельными прямыми немного поработали и к ним ещё вернёмся. Случай совпадающих прямых малоинтересен, поэтому перейдём к задаче, которая хорошо знакома вам из школьной программы:
Видео:Уравнение параллельной прямойСкачать

Уравнение параллельной прямой
Альтернативная формула:
Прямая, проходящая через точку M1(x1; y1) и параллельная прямой Ax+By+C=0 , представляется уравнением
назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).
Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника 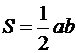
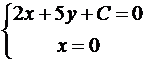
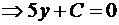
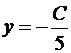
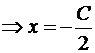
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 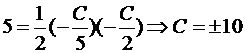
Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /7x – 4 /7 (здесь a = 5 /7). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .
Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.
Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).
Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Уравнение прямой, проходящей через заданную точку параллельно заданной прямой.
Эта статья является развернутым ответом на вопрос: «Как составить уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой»? Сначала приведена необходимая теория, после чего разобраны решения характерных задач. В заключении разобрано нахождение уравнений прямой, проходящей через заданную точку трехмерного пространства параллельно заданной прямой.
Навигация по странице.
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой.
Чтобы составление уравнения прямой, проходящей через заданную точку плоскости параллельно заданной прямой, не вызвало затруднений, вспомним важные факты.
Аксиома параллельных прямых гласит: на плоскости через точку, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Таким образом, мы можем определить конкретную прямую a на плоскости, указав прямую линию b , которой параллельна прямая a , и точку М1 , не лежащую на прямой b , через которую проходит прямая a .
Поставим перед собой следующую задачу.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy . Пусть в этой системе координат задана точка 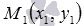
Решим поставленную задачу.
Из условия мы знаем координаты точки М1 , через которую проходит прямая a . Этих данных не достаточно, чтобы написать уравнение прямой a .
Нам еще нужно знать
Как же их найти?
По условию прямая a параллельна прямой b , тогда, на основании необходимого и достаточного условия параллельности двух прямых на плоскости, в качестве направляющего вектора прямой a мы можем принять направляющий вектор прямой b , в качестве нормального вектора прямой a мы можем взять нормальный вектор прямой b , а угловой коэффициент прямой a равен угловому коэффициенту прямой b (или они оба бесконечны).
Таким образом, чтобы в прямоугольной системе координат на плоскости написать уравнение прямой a , проходящей через заданную точку 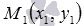
- или координаты направляющего вектора прямой b (
),
- или координаты нормального вектора прямой b (
),
- или угловой коэффициент прямой b (
),
принять их соответственно в качестве
- координат направляющего вектора прямой a (
),
- координат нормального вектора прямой a (
),
- углового коэффициента прямой a (
),
и записать требуемое уравнение прямой a соответственно в виде
или
,
,
.
Внесем ясности – приведем примеры с подробными решениями на каждый случай.
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 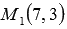
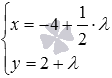
Из параметрических уравнений прямой 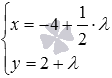
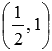
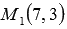
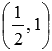
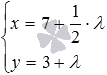
Это и есть искомые уравнения прямой, проходящей через заданную точку 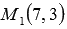
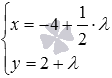
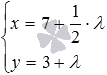
Иногда требуется составить уравнение прямой определенного вида, проходящей через заданную точку плоскости параллельно заданной прямой. В этом случае сначала записываем уравнение прямой, которое проще всего получить, после чего приводим его к нужному виду.
Составьте уравнение прямой в отрезках, если эта прямая в прямоугольной системе координат Oxy проходит через точку плоскости с координатами 
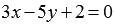
Очевидно, нормальным вектором прямой, общее уравнение которой имеет вид 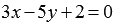
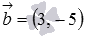

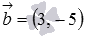
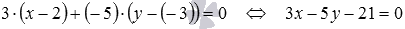

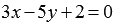
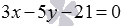
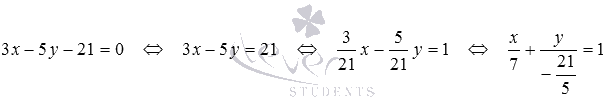
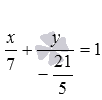
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 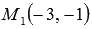
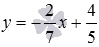
Мы знаем, что угловые коэффициенты параллельных прямых равны (или бесконечны), тогда 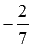
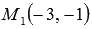
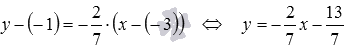
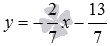
Итак, уравнение прямой a , проходящей через заданную точку плоскости M1 параллельно заданной прямой b , проще всего записывать в таком виде, в котором записано уравнение заданной прямой b .
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнения прямой, проходящей через заданную точку пространства параллельно заданной прямой.
В трехмерном пространстве через точку М1 , не лежащую на прямой b , проходит единственная прямая a , параллельная прямой b . Таким образом, прямую в пространстве можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана прямая b некоторыми уравнениями прямой в пространстве и точка 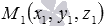
Направляющим вектором прямой a является направляющий вектор прямой b . Таким образом, по известным уравнениям прямой b мы можем определить координаты ее направляющего вектора, а, следовательно, и координаты направляющего вектора прямой a . После этого мы можем записать канонические уравнения прямой a в пространстве и параметрические уравнения прямой a в пространстве, так как известны координаты точки, лежащей на прямой a , и координаты направляющего вектора прямой a .
Рассмотрим решения примеров.
Напишите уравнения прямой, которая проходит через начало прямоугольной системы координат Oxyz в трехмерном пространстве параллельно прямой 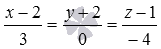
Очевидно, направляющим вектором прямой 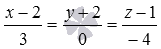
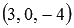
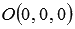
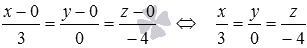
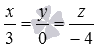
От канонических уравнений прямой a при необходимости можно будет перейти к уравнениям двух плоскостей, пересекающихся по прямой a .
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы три точки 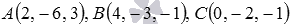
Направляющим вектором прямой, проходящей через точку С параллельно прямой АВ , является вектор 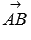
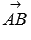
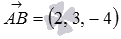
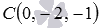
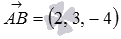
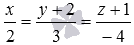
Осталось получить уравнения двух пересекающихся плоскостей, задающих эту прямую:
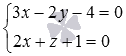
🎥 Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Составляем уравнение прямой по точкамСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Общее уравнение прямой"Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Параллельные прямые | Математика | TutorOnlineСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать





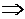
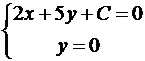
 ),
),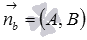 ),
),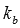 ),
),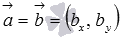 ),
),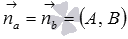 ),
),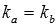 ),
),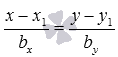 или
или 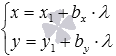 ,
,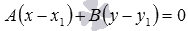 ,
,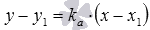 .
.