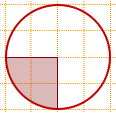
Вопрос по геометрии:
Найдите площадь заштрихованной части круга если радиус меньшей окружности равен 2см
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Пусть R — радиус большого круга. r — радиус маленького. По рисунку видно, что R = 2r = 4 см. Найдем площади кругов: Sб = Pi*R^2 = 16Pi Sм = Pi*r^2 = 4Pi Площадь заштрихованной области будет равна разности площадей большого и маленького кругов. Sобл = 16Pi — 4Pi = 12Pi = 37.6987 (см^2)
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Площадь круга. Математика 6 класс.Скачать

На клетчатой бумаге нарисованы два круга
Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):
Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
Разделим результат на число Пи и запишем ответ.
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.
Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см 2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см 2 .
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.
Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
Выразим площадь большего круга, так как его радиус равен 6х:
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см 2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см 2 .
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.
Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3 ∙ х, то
Выразим площадь большего круга. Так как его радиус равен 4 ∙ х, то
Разделим площадь большего на площадь меньшего:
То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см 2 .
Вычислим радиус меньшего круга. Его площадь равна 9, значит,
Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:
Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:
Определяем площадь большего круга:
Находим разность: 16 – 9 = 7 см 2
На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.
В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?
По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.
Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
С уважением, автор проекта Александр Крутицких.
Видео:Красивая геометрия ➜ Найдите площадь закрашенной части кругаСкачать
Круг на клетчатой бумаге
Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.
Для решения обеих задач надо определить величину соответствующего ему центрального угла.
Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.
Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.
Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).
Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).
1) На клетчатой бумаге изображён круг площадью 60.
Найти площадь заштрихованного сектора.
Так как центральный угол, соответствующий данному сектору, равен 90º, то
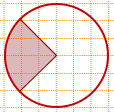
Какова площадь круга, если площадь заштрихованного сектора равна 17?
Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.
Следовательно, площадь сектора составляет 1/4 от площади круга: Sкруга=Sсектора:(1/4)=17·4=68.
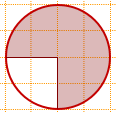
Площадь заштрихованного сектора составляет 3/4 площади круга.
Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).
Так как 45° составляет от 360° 1/8 часть, то

Найдите площадь заштрихованного сектора.
Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.
Sзакрашенного сектора=Sнезакрашенного сектора-Sкруга=96-12=84.
А как определить на клетчатой бумаге центральные углы в 60° и 30°?
Можно рассуждать следующим образом.
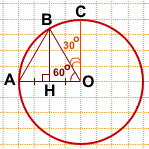
Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.
Но AO=BO (как радиусы).
Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.
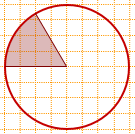
Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и Sсектора=Sкруга:6=30:6=5.
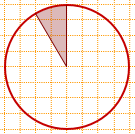
Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.
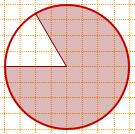
Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.
Следовательно, на площадь закрашенной части приходится 5/6 круга:
В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.
9) 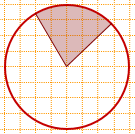
площадь заштрихованного сектора составляет
1/12+1/8=5/24 площади круга, то есть
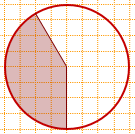
площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,
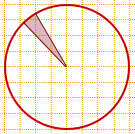
площадь заштрихованного сектора составляет 1/24 площади круга
📸 Видео
Найдите площадь закрашенной фигуры ★ 2 способа решения ★ Задание 3 ЕГЭ профильСкачать

КАК НАЙТИ ПЛОЩАДЬ КРУГА, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР? Примеры | МАТЕМАТИКА 6 классСкачать

Лучший способ найти площадь кругаСкачать

Площадь круга. Практическая часть - решение задачи. 6 класс.Скачать
Длина окружности. Площадь круга. 6 класс.Скачать

Площадь сектора и сегмента. 9 класс.Скачать

Задача на 5 секунд. Найти площадь заштрихованной фигурыСкачать

Как найти площадь закрашенной фигуры? Несложная геометрическая задачаСкачать

Найдите площадь закрашенной части полукругаСкачать

Длина окружности. Математика 6 класс.Скачать

Окружность и круг, 6 классСкачать

ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Найдите площадь закрашенной фигурыСкачать

Самый простой способ нахождения площадиСкачать

На клетчатой бумаге изображены два круга. Найдите площадь заштрихованной фигуры.Скачать

Найдите площадь кругаСкачать

Площадь фигурыСкачать

17 задание ОГЭ. 17.1.4. Окружность, круг и их элементыСкачать