Найдите периметр криволинейного треугольника

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

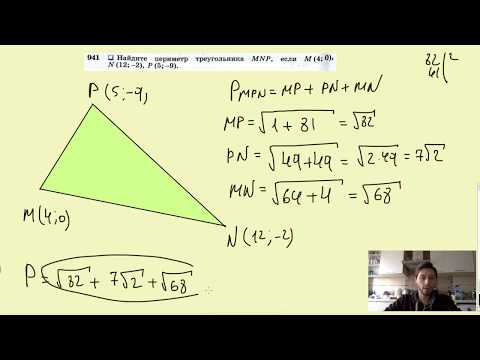
Видео:№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать

Длина дуги, угол между линиями, площадь области на поверхности

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Краткие теоретические сведения

Зная первую квадратичную форму поверхности, мы можем решить три задачи:

2. Найти угол между двумя линиями на поверхности в точке их пересечения:
Если две линии, лежащие на поверхности с первой квадратичной формой $I_1=E,du^2+2F,du,dv+G,dv^2$, пересекаются в некоторой точке $P$ поверхности и имеют в этой точке направления $(du:dv)$ и $(delta u:delta v)$, то косинус угла между ними определяется по формуле: begin mbox,varphi = displaystylefrac<sqrtcdotsqrt> \ mbox,varphi = displaystylefrac<sqrtcdotsqrt>. end Говорим, что кривая на поверхности $vec=vec(u,v)$ в точке $(u,v)$ имеет направление $(du:dv)$, если вектор $dvec=vec_udu+vec_vdv$ является касательным вектором кривой в этой точке.

3. Найти площадь области $Omega$ на поверхности: begin S = iintlimits_sqrtdu,dv, end где $D$ — прообраз $Omega$ на плоскости $(u,v)$.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Решение задач

Задача 1 (почти Феденко 684)

Найти длину дуги кривой, заданной уравнениями $v=3u$ на поверхности с первой квадратичной формой begin I_1=du^2+frac19,mbox^2u,dv^2 end между точками $M_1(u_1,v_1)$ и $M_2(u_2,v_2)$.

Решение задачи 1

Задача 2 (почти Феденко 682)

Под каким углом пересекаются линии $$ u+v=a, ,, u-v=a,$$ лежащие на поверхности: begin x=u,mboxv, ,, y=u,mbox,v, ,, z=au. end

Решение задачи 2

Первая квадратичная форма данной поверхности: begin I_1=(1+a^2),du^2+u^2,dv^2. end

Данные линии пересекаются в точке: begin left < beginu+v&=a,\ u-v&=a. end right. quad Rightarrow quad P(u=a,v=0). end

Направления данных линий: begin du+dv=0, ,, delta u-delta v=0,, Rightarrow end begin du = -dv, ,, delta u = delta v. end

Задача 3

Дана поверхность: $$z=axy.$$ Найти углы между координатными линиями.

Решение задачи 3

Координатные линии на данной поверхности задаются уравнениями: $x=x_0$, $y=y_0$. Запишем коэффициенты первой квадратичной формы: begin &E=1+(z_x)^2=1+a^2y^2,\ &F=z_xz_y=a^2xy, \ &G=1+(z_y)^2=1+a^2x^2. end

Направления координатных линий: begin &x=x_0 ,, Rightarrow dx=0,\ &y=y_0 ,, Rightarrow delta y=0. end

Задача 4 (Дополнение к Задаче 3)

Как мы вывели в примере выше, угол между координатными линиями равен

Из формулы следует, что координатная сеть поверхности ортогональна (координатные линии пересекаются под прямым углом), тогда и только тогда, когда $F$=0.

Задача 5 (Феденко 683)

Найти периметр и внутренние углы криволинейного треугольника $$ u=pm av^2/2,,, v=1,$$ расположенного на поверхности $$I_1=du^2+(u^2+a^2)dv^2.$$

Вершины треугольника: begin &A(u=0,, v=0),\ &B(u=-frac,, v=1), \ &C(u=frac,, v=1). end

Зная координаты вершин и уравнения сторон, найдем длины дуг, составляющих стороны треугольника $ABC$, и углы между линиями в точках их пересечения, то есть в вершинах треугольника: begin &s_1 = |BC| = a,\ &s_2 = |AC| = frac76 a,\ &s_3 = |BC| = frac76 a,\ &P_=s_1+s_2+s_3=fraca. end begin &mbox,A = 1, ,, mbox,B=mbox,C=frac23. end

Видео:Найдите периметр треугольникаСкачать

Задание №4. Начала интегрального исчисления, простейшие дифференциальные уравнения, основы теории числовых и функциональных рядов

Задание №4. Начала интегрального исчисления, простейшие дифференциальные уравнения, основы теории числовых и функциональных рядов.

I. Вычисление неопределенных интегралов

I.1. Применение основной таблицы интегралов. Вычислить интегралы:

1. ; 2. ; 3. ; 4. ;

5. ; 6. ; 7. 8. ;

9. ; 10.

I.2. Замена переменных в неопределенном интеграле. Вычислить интегралы:

1. ; 2. ; 3. ; 4. ;

5. ; 6. ; 7. ; 8. ;

9. ; 10. ; 11. ; 12. ; 13. ;

14. ; 15. ; 16. .

I.3. Интегрирование по частям. Вычислить интегралы:

1. ; 2. ; 3. ; 4. ; 5. ;

6. ; 7. ; 8. ; 9. ; 10.

I.4. Интегрирование рациональных функций:

1. ; 2. ; 3. ; 4. ;

5. ; 6. ; 7. ; 8) ; 9) ;

10) ; 11) ; 12)

I.5. Интегрирование иррациональных функций:

1. ; 2) ; 3) ; 4) ;

5) ; 6)

I.6. Интегрирование тригонометрических функций:

1. ; 2) ; 3) ; 4) ; 5) ;

6) ; 7) ; 8) ; 9) ;

10)

I.7. Интегрирование показательных и логарифмических функций:

1) ; 2) ; 3) ; 4) ; 5)

6) ; 7) ; 8)

II. Вычисление определенных интегралов.

II.1. Применение формулы Ньютона-Лейбница:

1) ; 2) ; 3) ; 4) ; 5) ;

6) ; 7) ; 8) ; 9) ; 10) ;

11) ; 12)

II.2. Замена переменной в определенном интеграле:

1) ; 2) ; 3) ; 4) ; 5) ;

6) ; 7) ; 8)

II.3. Средние значения функций.

Вычислить среднее значение функций в заданном сегменте:

1) в сегменте [1;4].

2) в сегменте [1;1,5].

3) и в сегменте [0;π].

4) Найти наибольшее и наименьшее значения функции

в сегменте [-1;1]

II.4. Вычисление площадей плоских фигур.

1). Вычислить площадь фигуры, ограниченной кривыми и .

2). Окружность разделена параболой на две части. Найти площади обеих частей.

3). Найти площадь фигуры, ограниченной дугой гиперболы и ее хордой, проведенной из фокуса перпендикулярно к действительной оси.

4). Вычислить площадь криволинейной трапеции с основанием [a;b], ограниченной линией .

5) Найти площадь фигуры, ограниченной замкнутой линией .

II.5. Вычисление длины дуги кривой.

1) Найти длину дуги линии от до .

2) Найти периметр одного из криволинейных треугольников, ограниченных осью абсцисс и линиями и .

3) На циклоиде найти точку, которая делит первую арку циклоиды по длине в отношении 1:3.

II.6. Вычисление площадей поверхностей и объемов тел вращения.

1) Вычислить площадь поверхности вращения параболы вокруг оси абсцисс от вершины до точки с абсциссой .

2) Вычислить площадь поверхности, образованной вращением одной арки синусоиды (от 0 до π) вокруг оси абсцисс.

3) Фигура, ограниченная гиперболой и прямой (h>0), вращается вокруг оси абсцисс. Найти объем тела вращения.

4) Симметричный параболический сегмент с основанием а и высотой h вращается вокруг основания. Вычислить объем тела вращения, которое при этом получается («лимон Кавальери»).

III. Решение простейших дифференциальных уравнений.

III.1. Уравнения с разделяющимися переменными.

Найти общие решения уравнений:

1) ; 2) ; 3) ; 4) ;

5) ; 6)

Найти частные решения уравнений, удовлетворяющие начальным условиям:

7) ; 8)

III.2. Однородные уравнения.

Найти общие решения уравнений:

1) ; 2) ; 3) ; 4) ; 5) $

6)

Найти частные решения уравнений, удовлетворяющие начальным условиям:

7) ; 8)

Ш.3. Линейные уравнения 1-го порядка.

Найти общие решения уравнений:

1) ; 2) ; 3) ; 4) ;

5)

Найти частные решения уравнений, удовлетворяющие начальным условиям:

6) ; 7)

Ш.4. Уравнения 2-го порядка.

Найти общие решения уравнений:

1) ; 2) ; 3) ; 4) ; 5) ;

6)

Найти частные решения уравнений, удовлетворяющие начальным условиям:

7) ; 8)

Ш.5. Уравнения 2-го порядка с постоянными коэффициентами.

Найти общие решения уравнений:

1) ; 2)

Найти частные решения уравнений, удовлетворяющие начальным условиям:

3) ; 4)

IV. Числовые и функциональные ряды

1) ; 2)

IV.2. Исследовать на сходимость ряды:

1) ; 2) ; 3)

IV.3. Доказать сходимость рядов с помощью признака Даламбера:

1) ; 2) ; 3)

IV.4. Доказать сходимость рядов с помощью признака Коши:

1) ; 2)

IV.5. Абсолютная и условная сходимость рядов. Выяснить, какие из рядов сходятся абсолютно, какие — условно, какие — расходятся:

1) ; 2) ; 3) ; 4)

IV.6. Определить области сходимости функциональных рядов:

1) ; 2) ; 3) ; 4)

IV.7. Убедиться, что данные ряды равномерно сходятся на всей оси ОХ:

1) 1+; 2) ; 3)

IV.8. Разложить функции в ряд Тейлора в окрестности указанных точек:

1) в окрестности точки х = 1;

2) в окрестности точки х = 2;

3) в окрестности точки х = 0;

4) в окрестности точки х = 0;

5) в окрестности точки х = 0;

6) в окрестности точки х = 0

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Нахождение периметра треугольника: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.

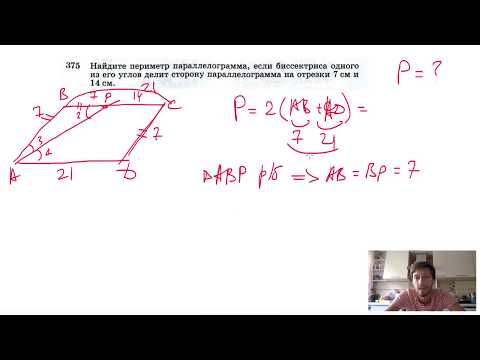
Видео:№375. Найдите периметр параллелограмма, если биссектриса одного из его углов делитСкачать

Формула вычисления периметра

Периметр (P) любого треугольника равняется сумме длин всех его сторон.

P = a + b + c

Периметр равнобедренного треугольника

Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:

P = a + 2b

Периметр равностороннего треугольника

Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:

P = 3a

Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Примеры задач

Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.

Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.

Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.

Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.

💡 Видео

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Найдите периметр прямоугольника на рисунке ★ Быстрый способ решенияСкачать

Задание № 941 — Геометрия 9 класс (Атанасян)Скачать

№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Диагностическая работа в формате ОГЭ. Задача-11Скачать

Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

ЕГЭ Математика Задание 6#27935Скачать

35. Геометрия на ЕГЭ по математике. Трапеция.Скачать

Прямоугольный треугольник площади криволинейныхСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

КАК БЫСТРО НАЙТИ ПЕРИМЕТР И ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА И КВАДРАТА ?Скачать