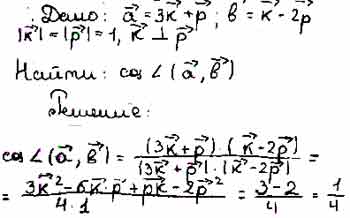Найдите косинус угла между векторами a 3k p и b k 2p (4 видео)

Найдите косинус угла между векторами a = 3k + р и b = к- 2р если k = р=1 и к_I_р.

В 19:57 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Содержание

Вопрос вызвавший трудности
Ответ подготовленный экспертами Учись.Ru
Онлайн калькулятор. Вычисление угла между векторами
Калькулятор для вычисления угла между векторами
Инструкция использования калькулятора для вычисления угла между векторами
Ввод даных в калькулятор для вычисления угла между векторами
Дополнительные возможности калькулятора для вычисления угла между векторами
Теория. Вычисление угла между векторами
Нахождение угла между векторами: онлайн калькулятор
Как найти угол между векторами с помощью онлайн-калькулятора
🎦 Видео

Видео:Как находить угол между векторамиСкачать

Вопрос вызвавший трудности

Видео:Угол между векторами | МатематикаСкачать

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Найдите косинус угла между векторами a = 3k + р и b = к- 2р если k = р=1 и к_I_р.

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

решение задания по геометрии

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Субботина Валерия Лаврентьевна — автор студенческих работ, заработанная сумма за прошлый месяц 52 000 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

Видео:Задача 3. Найти косинус угла между векторами.Скачать

Онлайн калькулятор. Вычисление угла между векторами

Этот онлайн калькулятор позволит вам очень просто найти угол между двумя векторами (косинус угла между векторами) для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между векторами и закрепить пройденный материал.

Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

Калькулятор для вычисления угла между векторами

Инструкция использования калькулятора для вычисления угла между векторами

Ввод даных в калькулятор для вычисления угла между векторами

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления угла между векторами

Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Угол между векторами. 9 класс.Скачать

Теория. Вычисление угла между векторами

Угол между двумя векторами a и b можно найти использовав следующую формулу:

cos α =	a · b
	\| a \|\| b \|

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Нахождение угла между векторами: онлайн калькулятор

Два вектора всегда образуют угол. Чтобы найти угол между двумя векторами на плоскости или в пространстве, нужно использовать формулу для скалярного произведения и знать длины векторов. Сначала вычисляется косинус угла между векторами, затем находится и сам угол.

Чтобы найти угол между векторами онлайн, не нужно самостоятельно производить громоздкие вычисления. Достаточно просто задать два вектора в удобной форме (точки или координаты) и нажать кнопку «рассчитать».

Видео:Косинус угла между векторами. Коллинеарность векторовСкачать

Как найти угол между векторами с помощью онлайн-калькулятора

Для нахождения угла между векторами с помощью нашего онлайн-калькулятора выполните несколько простых действий:

Укажите размерность векторов. Это может быть плоскость или пространство.
Определитесь с формой представления векторов. Их можно задать координатами либо точками:
В соответствующие поля введите значения векторов и нажмите «Рассчитать».
Рассмотрим наглядный пример с произвольными значениями. Пусть у нас есть два вектора на плоскости, заданные координатами:

После того, как мы нажмем «Рассчитать», калькулятор выдаст решение с пояснением: