Найдите длину сумму векторов a b изображенных на

Геометрия | 5 — 9 классы

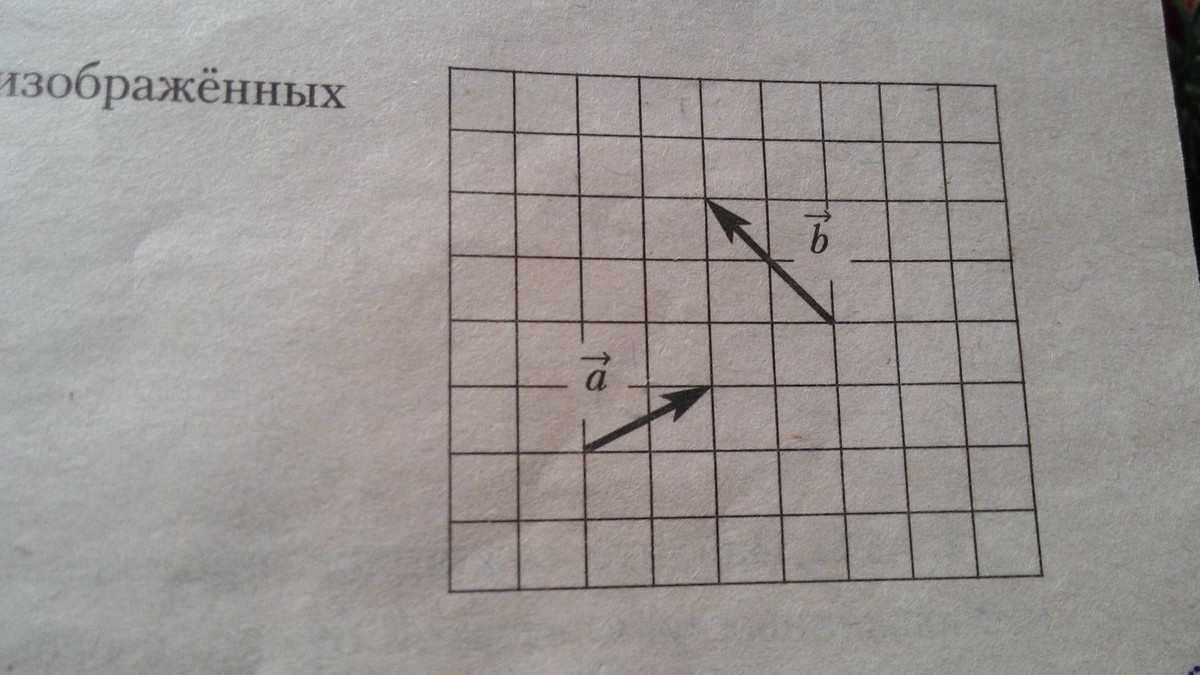
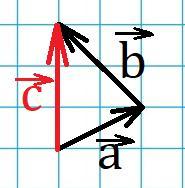
Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1.

Длина $displaystyle vec$ равна 3·1 = 3 т.

К. размер клетки 1 на 1.

Видео:егэ векторы решу егэ все задания №2 профильСкачать

Найдите площадь трапеции , изображенной на клетчатой бумаге с размером клетки 1см× 1см Ответ дайте в квадратных см?

Найдите площадь трапеции , изображенной на клетчатой бумаге с размером клетки 1см× 1см Ответ дайте в квадратных см.

Видео:Задача 2 из проекта демоверсии ЕГЭ 2024 по профильной математикеСкачать

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см?

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

На клетчатой бумаге с размером клетки 1×1 изоброжена трапеция ?

На клетчатой бумаге с размером клетки 1×1 изоброжена трапеция .

Найдите длину ее средней линии.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

На клетчатой бумаге с размером клетки 1х1 изображена трапеция?

На клетчатой бумаге с размером клетки 1х1 изображена трапеция.

Найдите длину её средней линии.

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см× 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см× 1 см.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Найдите (в см ^ 2) площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1× 1 см?

Найдите (в см ^ 2) площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1× 1 см.

Видео:Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать

Найдите (в см ^ 22) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 22) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:Длина вектора через координаты. 9 класс.Скачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:МОДУЛЬ ВЕКТОРА длина вектора 10 и 11 классСкачать

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Видео:Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник Найдите длину его гипотенузы?

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник Найдите длину его гипотенузы.

На этой странице вы найдете ответ на вопрос Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

1. Р(ABDE) = AB + BD + DE + EAР(BEDC) = BE + ED + DC + CBодна сторона DE = ED для этих четырехугольников общая. BD = BE по условию. Из равенства углов следует, что треугольники BCD и BAE равны (по стороне и двум прилежащим к ней углам. )BC = BA и ..

Вершины треугольника лежат на окружности, значит его углы вписанные. Вписанный угол равен половине градусной меры дуги, на которую он опирается. Значит дуга АВ равна удвоенной градусной мере угла С, опирающегося на эту дугу.

О — центр основания. DO = 8 — высота пирамиды. Пусть Н — середина ВС. Тогда, AH⊥BC как медиана и высота равностороннего треугольника, DH⊥ВС как медиана и высота равнобедренного треугольника. ⇒ ∠DHA — линейный угол двугранного угла при ребре основ..

Угол С = 112 Угол аов = 180 — (24 + 32) = 124 Угол вос = 180 — (32 + 56) = 92 Угол соа = 180 — (24 + 56) = 100.

По условию СМ перпендикулярна АВ. Значит, СМ высота ( перпендикулярна) и медиана — т. К. М — середина. Если высота треугольника одновременно и его медиана, то этот треугольник –равнобедренный. Следовательно, ∆ АСВ равнобедренный, и АС = ВС = 8 см..

1. Центральным углом называется угол, вершиной которого является центр окружности, сторонами — радиусы. Величинацентральногоугларавнаугловойвеличине дуги, накоторую он опирается. 2. Вписанным углом называется угол, вершина которого лежит на окружно..

BO = 18 — 14 = 4 см CP = 18 — 12 = 6 см PO = 18 — 4 — 6 = 8 cм.

Презнания гасударством способность физических лиц (граждан) и юрестических лиц иметь права инести обязанности, предосмотрение и допускаемые законы.

R = 10смh = 5смдлина окружности основанияL = 2pi * RSбок = L * h = 2pi * R * h = 2pi * 10 * 5 = 100Пи Или 314см2.

Диагонали прямоугольника равны, при пересечении делятся пополам и со сторонами образуют равнобедренные треугольники. Углы при основании равнобедренного треугольника равны. ∠СОD = ∠АОВ = 50° — вертикальные. Сумма углов треугольника 180°. Углы при ..

Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Сумма векторов. Длина вектора. Задачи!

Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.

Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:

Вектор — это направленный отрезок.

Все векторы, имеющие одинаковое направление и равные по длине являются равными.

*Все представленные выше четыре вектора равны!

То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.

Вектор может быть обозначен латинскими заглавными буквами, например:

При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.

Ещё вектор обозначается одной буквой латинского алфавита (прописной):

Возможно также обозначение без стрелок:

Суммой двух векторов АВ и ВС будет являться вектор АС .

Записывается как АВ + ВС = АС .

Это правило называется – правилом треугольника.

То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).

Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:

Перенесём вектор b, или по-другому – построим равный ему:

Как находится сумма нескольких векторов? По тому же принципу:

Это правило является следствием изложенного выше.

Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a, и мы можем построить вектор, который будет являться их суммой:

Ещё немного важной информации, необходимой для решения задач.

Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:

Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.

Пусть даны два вектора, найдём их разность:

Мы построили вектор противоположный вектору b, и нашли разность.

Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:

То есть, координаты вектора представляют собой пару чисел.

И координаты векторов имеют вид:

Модулем вектора называется его длина, определяется по формуле:

Формула для определения длины вектора, если известны координаты его начала и конца:

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО .

Найдём вектор, который будет являться результатом АО – ВО:

АО – ВО = АО +(– ВО )= АВ

То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ + AD .

Найдём вектор, который будет являться суммой векторов AD и AB . Вектор BC равен вектору AD . Значит AB + AD = AB + BC = AC

Длина вектора AC это длина диагонали ромба АС, она равна 16.

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО + ВО .

Найдём вектор, который будет являться суммой векторов АО и ВО . Вектор ВО равен вектору OD, з начит

Длина вектора AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:

По теореме Пифагора:

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО – ВО .

Найдём вектор, который будет являться результатом АО – ВО :

Длина вектора АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:

По теореме Пифагора:

Стороны правильного треугольника ABC равны 3.

Найдите длину вектора АВ – АС .

Найдём результат разности векторов:

Длина вектора СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.

27663. Найдите длину вектора а (6;8).

27664. Найдите квадрат длины вектора АВ .

27707. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора АС .

27708. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов AB и AD .

27709. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов AB и AD .

27711. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов АО и ВО .

27713. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ .

27715. Диагонали ромба ABCD равны 12 и 16.

Найдите длину вектора АВ – AD .

27716. Диагонали ромба ABCD равны 12 и 16.

Найдите длину вектора АВ – АС .

Стороны правильного треугольника ABC равны 2√3. Найдите длину вектора АВ + АС .

В будущем мы продолжим рассматривать задачи с векторами, не пропустите! Задания будут связаны с координатами векторов, скалярным произведением.

На этом всё. Успеха вам!

С уважением, Александр

Вступительный экзамен по математике. Преподаватели приглашают первого абитуриента:
— Сколько будет два плюс два?
— Три! — Нет! — Пять! — Нет! — Шесть!
— Неправильно! Да… дурак, но ищущий… берем!
Заходит второй абитуриент:
— Сколько будет два плюс два?
— Три! — Нет! — Три! — Нет! — Три!
— Неправильно! Да… дурак, но настырный… берем!
Заходит третий абитуриент:
— Сколько будет два плюс два?
— Четыре, конечно!
— Да… умный. Но мест уже нет!

Видео:Полный разбор задач с векторами №2 ЕГЭ ПРОФИЛЬ 2024 | Профильная математика ЕГЭ 2024 | УМСКУЛСкачать

Как найти сумму векторов

Видео:Интенсив ВЕКТОРЫ || День 4 || Координатные методыСкачать

Формула

Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Примеры нахождения суммы векторов

Задание. Найти сумму векторов $bar+bar$, $bar=(2;0)$ и $bar=(1;3)$

Решение. Для нахождения суммы векторов, сложим их соответствующие координаты

Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:

Видео:Модуль вектора. Длина вектора.Скачать

Остались вопросы?

Здесь вы найдете ответы.

Поможем выполнить
любую работу

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Все еще сложно?

Наши эксперты помогут разобраться

Не получается написать работу самому?

Доверь это кандидату наук!

Ищещь ответ на вопрос с которым нужна помощь?

📸 Видео

Сложение и вычитание векторов через координаты. Практическая часть. 11 класс.Скачать

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

КВАДРАТ ДЛИНЫ ВЕКТОРА ?/ Новое задание из ЕГЭ разбор #профиль #егэ #27731Скачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать