Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 11.
Это задание ещё не решено, приводим решение прототипа.
Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.
Угол A является прямым, он опирается на диагональ BD, которая является диаметром:
- Найти диагональ прямоугольника вписанного в окружность радиуса
- Найти диагональ прямоугольника вписанного в окружность радиуса
- Прямоугольник. Онлайн калькулятор
- Свойства прямоугольника
- Диагональ прямоугольника
- Окружность, описанная около прямоугольника
- Формула радиуса окружности описанной около прямоугольника
- Периметр прямоугольника
- Формулы сторон прямоугольника через его диагональ и периметр
- Признаки прямоугольника
- Найдите диагональ прямоугольника, вписанного в окружность радиуса 6 см.
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен…
- Вместе с этой задачей также решают:
- 📹 Видео
Видео:Пробный ЕГЭ 2013 В6 диагональ прямоугольника ABCD #6Скачать

Найти диагональ прямоугольника вписанного в окружность радиуса
Видео:2089 Найдите диагональ прямоугольника вписанного в окружность радиус которой равен 5Скачать

Найти диагональ прямоугольника вписанного в окружность радиуса
Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 11.
Это задание ещё не решено, приводим решение прототипа.
Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.
Угол A является прямым, он опирается на диагональ BD, которая является диаметром:
Видео:Задание 3 ЕГЭ по математике. Урок 70Скачать

Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Видео:Задание 3 ЕГЭ по математике. Урок 47Скачать

Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
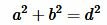 . . | (1) |
Из равенства (1) найдем d:
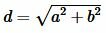 . . | (2) |
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
 |
Ответ:
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Видео:Задание 3 ЕГЭ по математике. Урок 46Скачать

Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac ) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac ) | (4) |
Пример 2. Стороны прямоугольника равны 
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя 
 |
 |
Ответ:
Видео:2095 Найдите сторону квадрата вписанного в окружность радиуса 18 корней из 2Скачать

Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
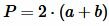 | (5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
 |
Ответ:
Видео:Радиус и диаметрСкачать

Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
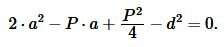 | (10) |
Вычислим дискриминант квадратного уравнения (10):
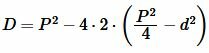 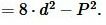 | (11) |
Сторона прямоугольника вычисляется из следующих формул:
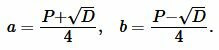 | (12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*). |
Пример 4. Диагональ прямоугольника равна 

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим 

 |
Подставляя значения 

 |
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения 

 |
Ответ: 
Видео:Решение задания 17 #2 для подготовки к сдаче ОГЭ 2020 по математикеСкачать

Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Видео:Диагональ прямоугольника. Математика. Геометрия.Скачать

Найдите диагональ прямоугольника, вписанного в окружность радиуса 6 см.
Видео:ПОДРОБНОЕ РЕШЕНИЕ ВОСЕМНАДЦАТОГО ЗАДАНИЯ ОГЭ МАТЕМАТИКА 2018Скачать
Ваш ответ
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

решение вопроса
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,962
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:17 задание ОГЭ по математикеСкачать

Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен…
Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен $7$ (см. рис.).
Объект авторского права ООО «Легион»
Видео:Задание 16 Часть 3Скачать

Вместе с этой задачей также решают:
В параллелограмме $ABCD$ $AB = 6, AD = 9, sinA = /$. Найдите большую высоту параллелограмма.
В треугольнике $ABC$ угол $C$ равен $90^°$, катет $AC=16$, $sin A= / $ (см. рис.). Найдите $AB$.
Площадь параллелограмма равна 160, две его стороны равны 10 и 20. Найдите большую высоту этого параллелограмма.
В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=12$, $cos A= / $ (см. рис.). Найдите $AB$.
📹 Видео
Задание 26 Вписанный квадратСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / прямоугольник / диагонали / решу егэСкачать

Как найти центр круга #2Скачать

Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать




