Способы решения навигационного треугольника скоростей. Во время подготовки и выполнения полета экипажу часто приходится решать навигационный треугольник скоростей. Решить треугольник – значит найти неизвестные его элементы по известным. Действительно, некоторые навигационные элементы (например, курс, истинная скорость) могут быть измерены с помощью приборов в полете, другие (например, скорость и направление ветра), могут быть получены от метеослужбы в аэропорту. Тогда неизвестные, но необходимые для навигации параметры можно определить, используя взаимосвязь элементов НТС.
Самый наглядный, но не самый удобный способ решения НТС – графический. Можно с помощью транспортира и линейки на листе бумаги в выбранном масштабе нарисовать меридиан и известные элементы НТС (например, векторы Vи U) так, чтобы их расположение (величина и направление относительно меридиана) соответствовало условиям задачи. Тогда, достроив НТС до конца (в приведенном примере – дорисовав W), можно просто измерить линейкой величину путевой скорости, а транспортиром – угол сноса, ФПУ и любые другие элементы.
На практике в полете НТС, конечно, не рисуют. В России на протяжении многих десятилетий в качестве такого инструмента используется навигационная линейка НЛ-10М. Разумеется, эти задачи можно решать и на калькуляторе по формулам, приведенным в соответствующих главах.
В навигации принято выделять четыре типовые задачи решения навигационного треугольника скоростей. Наиболее часто приходится решать первые две из них, которые и будут здесь подробно рассмотрены.
Расчет путевой скорости и угла сноса по известному ветру. Такая задача решается во время предполетной подготовки, когда пилот рассчитывает навигационные элементы и заполняет штурманский бортовой журнал (операционный план полета- operation flight plan) – его левую часть, содержащую предполетные расчеты. Для каждого участка маршрута (от одного ППМ до другого) необходимо рассчитать УС и курс, который будет при данном ветре обеспечивать полет по ЛЗП, путевую скорость и время полета.
Исходными данными для задачи являются следующие величины:
— истинная воздушная скорость V. Для каждого типа ВС из его Руководства по летной эксплуатации (РЛЭ) примерно известно, какая истинная скорость V будет иметь место на данной высоте полета по маршруту;
— заданный путевой угол может быть измерен на карте, а на радионавигационных картах магнитные путевые углы (ЗМПУ) уже напечатаны для каждого участка маршрута;
— направление и скорость ветра. Эти данные экипаж получает во время метеоконсультации в аэропорту. Ветер по маршрутам, по которым выполняются полеты из данного аэропорта, включают в специальный бланк, находящийся в штурманской комнате аэропорта. Направление ветра в нем приводится метеорологическое;
— длина участка маршрута необходима для расчета времени полета на участке маршрута и может быть измерена или уже напечатана на карте;
— магнитное склонение определяется по карте с помощью изогон и необходимо толькодля перевода метеорологического направления ветра в навигационное.
В навигации общеприняты и предполагаются известными следующие единицы измерения: (расстояния – км, скорость – км/ч, время — минуты, угловые величины – градусы).
Рассмотрим порядок решения задачи на примере со следующими исходными данными:
— магнитный курс, при выдерживании которого ВС будет лететь по ЛЗП;
— время полета на участке маршрута.
1. Рассчитывается навигационное направление ветра:
δн = δ ± 180 °– ΔМ = 290 – 180 – (–4) = 114.
2. Рассчитывается угол ветра.
Из НТС известно, что УВ= δн – ФМПУ. Во время предполетной подготовки, когда решается эта задача, самолет еще не летит и, конечно, никакого фактического путевого угла (ФМПУ) еще не существует. Но ведь смысл данной задачи заключается в расчете такого курса, при котором самолет следовал по ЛЗП, то есть, чтобы выполнялось условие ФМПУ=ЗМПУ, поэтому в задаче этого типа угол ветра:
УВ= δн –ЗМПУ = 114 – 232 = – 118 = 242º.
Очевидно, что при таком УВ ветер дует влево и назад относительно направления полета. Следовательно, УС должен быть отрицательным (будет сносить влево), а путевая скорость получится меньше истинной.
Находят угол сноса и путевую скорость с использованием теоремы синусов). Из нее следует:
Расчет по этим формулам можно выполнить как на калькуляторе, так и на НЛ-10М.
При описании расчетов на НЛ-10М обычно используются небольшие рисунки шкал и устанавливаемых на них значений, описывающие алгоритм решения. Эти рисунки (схемки) принято называть «ключами» для решения задачи на НЛ-10.
На рис. 3.11 изображен ключ для определения УС и W. Кстати, этот ключ выгравирован и на самой НЛ-10.
Рис. 3.11. Определение угла сноса и путевой скорости (ключ)
Для его использования на шкале 5 (нумерация и названия шкал приведены в главе 4) визиркой устанавливается значение V и перемещением движка под визирную линию подводят значение УВ на шкале 3 (синусов). Затем визирка перемещается на значение U по шкале 5 и напротив нее по шкале 3 отсчитывается УС.
После этого в уме определяется КУВ=УВ+УС, на его значение передвигается визирка (по шкале 3) и напротив нее по шкале 5 отсчитывается W. Необходимо сделать несколько полезных замечаний, касающихся расчета на линейке. Во-первых, если УВ оказался больше 180°, его невозможно установить на шкале линейки. В этом случае этот же угол нужно представить как отрицательный: 242 = – 118. На шкале устанавливают 118. Знак на линейке, конечно, не устанавливают, но помнят, что УВ с минусом. Кстати это автоматически означает, что и УС будет отрицательным.
Во-вторых, если УС оказался меньше 5, его придется отсчитывать по шкале 4 (тангенсов). Это объясняется тем, что синусы и тангенсы малых углов примерно равны.
В-третьих, складывать УВ (точнее, то его значение, которое устанавливается на шкале, в нашем примере 118) и УС можно по модулю, невзирая на знаки. Это следует из того, что, если УВ представлен лежащим в диапазоне от –180° до +180°, то знаки УВ и УС всегда одинаковы.
В-четвертых, нужно помнить, что хотя УС и принято в ответе округлять до градуса, для расчета КУВ желательно его использовать более точно (учесть доли градуса). В противном случае W может быть определена с погрешностью. Особенно это важно, когда УС мал.
4. Рассчитывают курс следования, который обеспечит выполнение полета по ЛЗП.
Из НТС следует, что МК=ФМПУ–УС. Поскольку для выполнения полета необходимо, чтобы ФМПУ был равен ЗМПУ, то
Для рассматриваемого примера
5. Рассчитывают время полета на участке.
Расчет выполняется по путевой скорости. Очевидно, что
При расчете на калькуляторе непосредственно по этой формуле время будет получено в часах, поскольку W измеряется в километрах в час. Чтобы получить время (как это требуется) в минутах, необходимо полученный результат умножить на 60 (количество минут в часе).
Определение ветра в полете. В рассмотренной задаче предполагалось, что ветер уже известен. Действительно, если задача решается во время предполетной подготовки, то используются прогностические скорость и направление ветра, полученные от метеорологов. Однако прогноз погоды по маршруту может быть неточен, и фактический ветер может значительно отличаться от прогностического. Поэтому одной из первых задач, которые решает экипаж после занятия заданной высоты, это определение фактических направления и скорости ветра.
Ветер можно определить разными способами на основе использования различных исходных данных: по двум углам сноса на различных курсах, по двум путевым скоростям и т.д. В гражданской авиации в транспортных полетах экипаж не имеет возможности произвольно менять курс только для того, чтобы измерить на этих курсах УС. Ведь ВС должно лететь по заданному маршруту. Поэтому в гражданской авиации получил распространение способ определения ветра по путевой скорости и углу сноса, измеренным на одном курсе.
Исходными данными для решения задачи являются следующие величины:
— курс полета может быть определен в полете с помощью курсовых приборов (компасов);
— истинная воздушная скорость должна быть рассчитана по измеренной в полете приборной воздушной скорости;
Путевая скорость и угол сноса могут быть непосредственно измерены в полете бортовым оборудованием (например, доплеровским измерителем скорости и сноса) или определены одним из способов, которые будут рассмотрены далее.
Необходимо найти направление и скорость ветра.
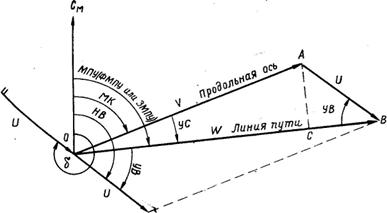
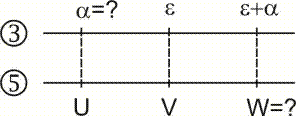
Математические соотношения, необходимые для решения данной задачи, могут быть получены с помощью рисунка (см. рис. 3.6) на котором изображен НТС с вершинами, обозначенными буквами О, А и С.
Пусть В — проекция точки А на вектор путевой скорости. Тогда из треугольника АВС имеем:
Из треугольника OAB AB=V sinα.
В свою очередь BC=OC–OB=W–Vcosα .
Величина, соответствующая отрезку ВС, называется продольной составляющей ветра. Это проекция вектора ветра на линию фактического пути (направление вектора W).
Поскольку скорость ветра обычно меньше (а часто в несколько раз меньше), чем скорость самолета, то абсолютная величина УС, как правило, невелика – единицы градусов. Лишь для малоскоростных ВС или при очень сильном ветре УС может достигать 10-20˚ . Косинусы малых углов близки к единице. Поэтому с достаточно высокой точностью можно считать, что V cos α ≈ V.
Погрешность за счет такого допущения обычно не превышает погрешностей измерения W и V. Например, если V=500 км/ч, а угол сноса 5°, то cos5° = 0,996, Vcos α = 498 км/ч. Разность (2 км/ч) в несколько раз меньше цены деления на шкале указателя скорости.
В связи с этим на практике при расчете ветра обычно принимают:
BC=OC–OB=W–Vcosα ≈W–V =Uэкв .
Разность путевой и истинной скоростей называется эквивалентным ветром и будет рассмотрена дальше.
Подставив полученные выражения для АВ и ВС в формулу получим:
Также из треугольника ОАВ (рис. 3.6) можно записать:
а из треугольника АВС: AB=Usinε.
Приравняв эти выражения и поделив обе части соотношения на произведение VU, получим:
Полученные выражения легко реализуются на калькуляторе и на НЛ-10М.
Рассмотрим ключ для решения задачи на навигационной линейке (рис. 3.12). На шкале 5 визирка устанавливается на Uэкв и движок перемещается так, чтобы с ним совпало значение УС на шкале 3 (синусов). Затем визирка перемещается на значение истинной скорости V по шкале 5 и напротив него по шкале 4 (тангенсов) отсчитывается так называемый острый угол ветра ε* (рис. 3.12, а). Дело в том, что на шкале тангенсов невозможно установить угол более 90° (а точнее, более 85°). Калькулятор при выполнении операции взятия арктангенса тоже выдает главное значение угла, то есть не превышающее по модулю 90°. Это значение и называют острым углом ветра. Затем (вторая часть ключа) движок перемещается так, чтобы на это же место (то есть напротив V) было установлено это же значение полученного ε*, но уже по шкале синусов. Вернув визирку на значение УС по шкале синусов, напротив него по шкале 5 можно отсчитать скорость ветра U (рис. 3.12, б)..
Рис. 3.12. Определение ветра
Таким образом, скорость реального ветра U уже найдена и теперь необходимо определить навигационное направление ветра. Полученный на НЛ-10 угол ε* всегда меньше 90°, поскольку в таких пределах оцифрована шкала тангенсов. Это просто острый угол между линией фактического пути (направлением вектора W) и линией, вдоль которой дует ветер. Для примера показан угол ветра и острый угол ветра для случая, когда ветер дует влево назад (рис. 3.13).
Рис. 3.13. Угол ветра и острый угол ветра
С помощью острого угла ветра ε* легко определить навигационное направление ветра. При этом целесообразно опираться не на формальные правила и формулы, а на здравый смысл и пространственное представление.
Первоначально необходимо определить направление полета, то есть фактический путевой угол βф, поскольку именно от этого направления отсчитывается ε. Очевидно, что: 84
Затем необходимо определить (с точностью до четверти) в каком направлении дует ветер относительно направления полета – вперед или назад, влево или вправо. Это ключевой момент в решении задачи, но он не представляет сложности.
Если путевая скорость W больше воздушной скорости V, то есть относительно земли ВС движется быстрее, чем относительно воздушной массы, значит ветер попутный, «помогает» полету, то есть дует вперед. В противном случае (W 0, то ветер дует вправо. Следовательно, вектор ветра лежит во II четверти, если отсчитывать четверти от направления ЛФП по часовой стрелке (см.рис. 3.14). В этом случае острый угол ветра ε* отсчитывается от направления, противоположного направлению W, то есть:
ФМПУ±180 = 320 –180=140°.
Поскольку вектор ветра расположен от этого направления в сторону против часовой стрелки, то направление ветра будет меньше на величину ε* :
Видео:Воздушная навигация.Навигационный треугольник скоростей-элементы и взаимозависимость.Скачать

УТЦ Ростов
Видео:Определение путевой скорости и угла сносаСкачать

Угол сноса
В данной статье описывается расчет угла бокового сноса ветром в зависимости от скорости и направления ветра, вводится понятие навигационного треугольника скоростей.
Видео:Вводная часть лекции по определению основных параметров навигационного треугольника скоростей.Скачать

Термины и определения

Путевая скорость – скорость воздушного судна относительно земли.
Магнитный курс (МК, heading) – это угол, заключенный между северным направлением меридиана, принятого за начало отсчета и продольной осью воздушного судна.
Магнитный путевой угол (МПУ, track) – это угол, заключенный между северным направлением меридиана, принятого за начало отсчета, и линией пути.
Навигационный ветер (НВ) – угол между северным направлением меридиана, принятого за начало отсчета и направлением, куда дует ветер.
Метеорологический ветер – угол между северным направлением меридиана, принятого за начало отсчета и направлением, откуда дует ветер.
Угол сноса (УС) – угол, заключенный между продольной осью самолета и линией пути. Отсчитывается от продольной оси самолета до линии пути вправо со знаком плюс и влево со знаком минус.
Курсовой угол ветра (КУВ) – угол, заключенный между линией пути (фактической или заданной) и направлением навигационного ветра. Отсчитывается от линии пути до направления ветра по ходу часовой стрелки от 0 до 360°.
Видео:Скорость полета самолетаСкачать
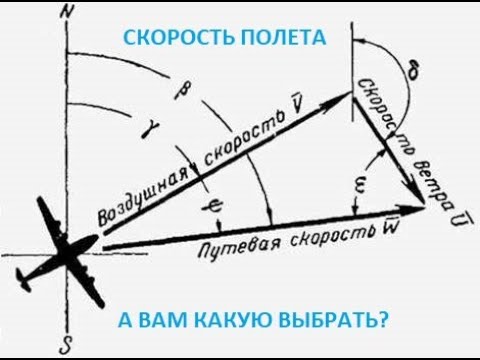
Навигационный треугольник скоростей
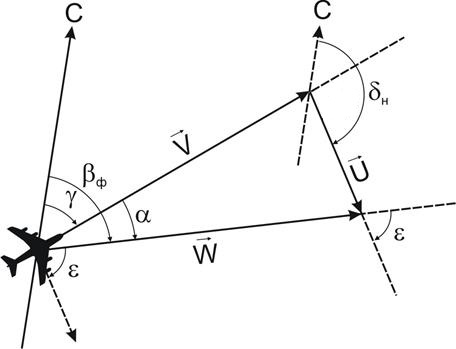
α – угол сноса
β ф – МПУ
δ н – навигационный ветер
ε – курсовой угол ветра
γ – магнитный курс
V – воздушная скорость
W – путевая скорость
U – скорость ветра
Самолет относительно воздушной массы перемещается с воздушной скоростью в направлении своей продольной оси. Одновременно под действием ветра он перемещается вместе с воздушной массой в направлении и со скоростью ее движения. В результате движение самолета относительно земной поверхности будет происходить по равнодействующей, построенной на слагаемых скоростях самолета и ветра. Таким образом, при полете с боковым ветром векторы воздушной скорости, путевой скорости и скорости ветра образуют треугольник, который называется навигационным треугольником скоростей. Каждый вектор характеризуется направлением и величиной.
Видео:Определение направления и скорости ветраСкачать

Расчеты
Между элементами навигационного треугольника скоростей существует следующая зависимость:
γ = β – (±α)
β = γ + (±α)
α = β – γ
W = V(соs(α)) + U(соs(ε))
ε = δ м ± 180° – β
δ м = β + ε ± 180°
При расчетах необходимо учитывать, что все величины необходимо привести к единому измерению. Например, скорости ветра и истинную воздушную скорость необходимо выразить в в узлах или метрах в секунду.
Видео:подсмотрено 2100. Лайфхак. Навигационный треугольник скоростейСкачать

Расчет в уме
Для простоты расчета используется методика максимального угла сноса. Для этого рассчитывается максимальный возможный угол сноса для текущего ветра, а потом вносится поправка на угол ветра.
Максимальный угол сноса равен:
α max ≈ (60 * U) / V
Максимальный угол сноса – это такой УС, при котором ветер был бы строго боковой (90 градусов относительно магнитного курса).
Пример: скорость ветра 15 узлов, истинная воздушная скорость 450 узлов. По формуле находим:
(60*15)/450=2
2 градуса – максимальный угол сноса.
Если ветер не строго боковой, то полученный результат умножаем на коэффициент, зависящий от курсового угла ветра (КУВ), равный синусу КУВ:
| КУВ | Коэффициент |
|---|---|
| 60° | 0,8 |
| 45° | 0,7 |
| 30° | 0,5 |
| 0 | 0° |
- Знак для значения угла сноса определяется исходя из направления ветра. Если ветер дует в правый борт, то знак “минус”, если в левый – “плюс”.
- Для следования по ЛЗП необходимо внести поправку в курс, равную УС, но противоположную по знаку
- Скорости U и V должны быть в одной размерности
- Приборная скорость не равна истинной
- М/с, для расчётов в уме, можно переводить в узлы простым умножением на 2
Видео:Маневренный планшет полная версияСкачать
Пример:
Найти угол сноса, если МПУ 130°, навигационный ветер на данной высоте 190°, 7м/с. Истинная скорость 220 узлов.
1) Приводим значения к единой системе счисления:
МПУ=130°;
Ветер 190°;
Скорость ветра 7 м/с = 14 узлов;
Vист = 220 узлов.
2) Находим курсовой угол ветра:
КУВ=НВ-МПУ=190°-130°=60°
3) Находим максимальный угол сноса:
УСmax=(60*14)/220=4°
4) Определяем коэффициент:
К=sin(КУВ)=sin(60°)=0,8
5) Получаем угол сноса
УС=УСmax*K=(+)4°*0,8=3°
Ответ: для поправки на ветер необходимо взять 3 градуса влево. МК=127°.
Видео:Штурманский расчёт/NavlogСкачать

Навигационный треугольник скоростей расчет
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
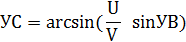
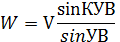
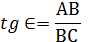
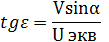
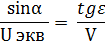
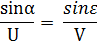



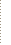

 Летательные аппараты » Самолетовождение » Навигационные элементы полета и их расчет » Навигационный треугольник скоростей, его элементы и их взаимозависимость
Летательные аппараты » Самолетовождение » Навигационные элементы полета и их расчет » Навигационный треугольник скоростей, его элементы и их взаимозависимость