Направление вектора ускорения при равномерном движении по окружности (4 видео)

Равномерное движение тела по окружности

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ( T ) — время, в течение которого тело совершает один полный оборот. Единица периода — ( [,T,] ) = 1 с.

Частота обращения ( (n) ) — число полных оборотов тела за одну секунду: ( n=N/t ) . Единица частоты обращения — ( [,n,] ) = 1 с -1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.

Связь между частотой и периодом обращения выражается формулой: ( n=1/T ) .

Пусть некоторое тело, движущееся по окружности, за время ( t ) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ( varphi ) .

Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость ( omega ) — физическая величина, равная отношению угла поворота ( varphi ) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ( omega=varphi/t ) . Единица угловой скорости — радиан в секунду, т.е. ( [,omega,] ) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ( 2pi ) . Поэтому ( omega=2pi/T ) .

Линейная скорость тела ( v ) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ( vec=l/t ) . За один оборот точка проходит путь, равный длине окружности. Поэтому ( vec=2pi!R/T ) . Связь между линейной и угловой скоростью выражается формулой: ( v=omega R ) .

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ( vec=frac<Deltavec> ) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ( a=frac ) . Так как ( v=omega R ) , то ( a=omega^2R ) .

При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

Содержание

ПРИМЕРЫ ЗАДАНИЙ
Часть 1
Часть 2
Движение по окружности
Угловая скорость
Нормальное ускорение
Тангенциальное ускорение
Кинематика. Равномерное движение по окружности.
🎦 Видео

Видео:Ускорение при равномерном движении по окружностиСкачать

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии ( R_1 ) от центра вращающегося колеса, равна ( v_1 ) . Чему равна скорость ( v_2 ) точки 2, находящейся от центра на расстоянии ( R_2=4R_1 ) ?

1) ( v_2=v_1 )
2) ( v_2=2v_1 )
3) ( v_2=0,25v_1 )
4) ( v_2=4v_1 )

3. Период обращения точки по окружности можно вычислить по формуле:

1) ( T=2pi!Rv )
2) ( T=2pi!R/v )
3) ( T=2pi v )
4) ( T=2pi/v )

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) ( omega=a^2R )
2) ( omega=vR^2 )
3) ( omega=vR )
4) ( omega=v/R )

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

1) 200 000 с
2) 3300 с
3) 3·10 -4 с
4) 5·10 -6 с

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) ( 1/T )
2) ( v^2/R )
3) ( v/R )
4) ( omega R )
5) ( 1/n )

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

Видео:Физика - движение по окружностиСкачать

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

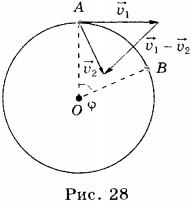
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Видео:Центростремительное ускорение. 9 класс.Скачать

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Видео:Линейная и угловая скорости при равномерном движении по окружностиСкачать

Кинематика. Равномерное движение по окружности.

Среди различных видов криволинейного движения особый интерес представляет равномерное движение тела по окружности. Это самый простой вид криволинейного движения. Вместе с тем любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности.

Такое движение совершают точки вращающихся колес, роторов турбин, искуственные спутники, вращающиеся по орбитам и т. д. При равномерном движении по окружности численное значение скорости остается постоянным. Однако направление скорости при таком движении непрерывно изменяется.

Скорость движения тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. В этом можно убедиться, наблюдая за работой точила, имеющего форму диска: прижав к вращающемуся камню конец стального прута можно увидеть отрывающиеся от камня раскаленные частицы. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной к окружности движутся также брызги от колес буксующего автомобиля.

Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различные направления, тогда как модуль скорости может быть или всюду одинаковым, или изменяться от точки к точке. Но даже если модуль скорости не изменяется, ее все равно нельзя считать постоянной. Ведь скорость – величина векторная, а для векторных величин модуль и направление одинаково важны. Поэтому криволинейное движение всегда ускоренное, даже если модуль скорости постоянен.

При криволинейном движении могут изменяться модуль скорости и ее направление. Криволинейное движение, при котором модуль скорости остается постоянным, называют равномерным криволинейным движением. Ускорение при таком движении связано только с изменением направления вектора скорости.

И модуль, и направление ускорения должны зависеть от формы кривлинейной траектории. Однако нет необходимости рассматривать каждую из ее бесчисленных форм. Представив каждый участок как отдельную окружность с некоторым радиусом, задача нахождения ускорения при криволинейном равномерном движении сведется к отысканию ускорения при равномерном движении тела по окружности.

Равномерное движение по окружности характеризуется периодом и частотой обращения.

Время, за которое тело делает один оборот, называют периодом обращения.

При равномерном движении по окружности период обращения определяется делением пройденного пути, т. е. длины окружности на скорость движения:

Величина, обратная периоду, называется частотой обращения, обозначается буквой ν. Число оборотов в единицу времени ν называют частотой обращения:

Из-за непрерывного изменения направления скорости, движущееся по окружности тело имеет ускорение, которое характеризует быстроту изменения ее направления, численное значение скорости в данном случае не меняется.

При равномерном движении тела по окружности ускорение в любой ее точке всегда направлено перпендикулярно скорости движения по радиусу окружности к ее центру и называется центростремительным ускорением.