Дата добавления: 2015-07-09 ; просмотров: 3586 ; Нарушение авторских прав
1. Напишите приложение, которое строит ряд окружностей. Центр окружностей совпадает с центром экрана. Число окружностей задается при первом вызове рекурсивного метода.
2. Напишите приложение, которое строит ряд квадратов. Центр квадратов совпадает с центром экрана. Число квадратов задается при первом вызове рекурсивного метода.
3. Напишите приложение, которое строит ряд окружностей по диагонали. Число окружностей задается при первом вызове рекурсивного метода.
4. Напишите приложение, которое строит ряд увеличивающихся окружностей по диагонали. Число окружностей задается при первом вызове рекурсивного метода.
5. Напишите приложение, которое строит ряд окружностей, центры которых лежат на окружности. Число окружностей задается при первом вызове рекурсивного метода.
6. Напишите приложение, которое строит ряд квадратов, центры которых лежат на окружности. Число квадратов задается при первом вызове рекурсивного метода.
7. Напишите приложение, которое строит ряд увеличивающихся окружностей, центры которых лежат на окружности. Число окружностей задается при первом вызове рекурсивного метода.
8. Напишите приложение, которое строит ряд увеличивающихся окружностей, центры которых лежат на спирали. Число окружностей задается при первом вызове рекурсивного метода.
9. Вычислить, используя рекурсию, выражение:
10. Напишите приложение, которое строит ряд окружностей. Число окружностей удваивается на каждом шаге (в рекурсивном методе происходит два рекурсивных вызова). Центры окружностей выбираются каждый раз произвольно (случайно). Линии связывают центры окружностей «предка» и «порожденных» от нее. Число рекурсий задается при первом вызове рекурсивного метода.
11. Напишите приложение, которое строит ряд увеличивающихся окружностей. Число окружностей удваивается на каждом шаге (в рекурсивном методе происходит два рекурсивных вызова). Центры окружностей выбираются каждый раз произвольно (случайно). Толщина линий также увеличивается. Число рекурсий задается при первом вызове рекурсивного метода.
12. Напишите приложение, которое строит ряд уменьшающихся окружностей. Число окружностей удваивается на каждом шаге (в рекурсивном методе происходит два рекурсивных вызова). Число рекурсий задается при первом вызове рекурсивного метода.
13. Напишите приложение, которое строит приведенное ниже изображение. Число рекурсий задается при первом вызове рекурсивного метода. На каждом шаге число окружностей увеличивается в четыре раза (в рекурсивном методе происходит четыре рекурсивных вызова).
14. Постройте ковер Серпинского.
Индивидуальные задания
повышенной сложности
Для решения геометрических задач повышенной сложности необходимо:
1) знать, как представляются на плоскости такие геометрические объекты, как точка, прямая, отрезок и окружность;
2) уметь находить уравнение прямой, соединяющей две заданные точки;
3) уметь определять координаты точки пересечения двух прямых;
4) знать, как провести перпендикуляр к прямой или определить, являются ли прямые параллельными;
5) уметь находить скалярное и векторное произведение;
6) находить площадь многоугольника;
7) уметь работать с фигурами на плоскости.
Напомним основные моменты, связанные с этими понятиями.
Каждую точку плоскости можно считать вектором с началом в точке (0,0). Обозначим через a=(x, y) вектор с координатами (x, y). Длина вектора (его модуль) вычисляется по формуле 
| x |
| y |
| a |
| b |
| φ |
| y1 |
| y2 |
| x1 |
| x2 |
Рис. 16.1. Иллюстрация к скалярному произведению векторов
Скалярное произведение двух векторов – это число, равное произведению модулей этих векторов на косинус угла между ними, (a,b)=|a| ∙ |b| ∙ cos φ. Если вектор a имеет координаты (x1, y1),а вектор b координаты – (x2, y2), то скалярное произведение вычисляется по формуле (a,b)= x1 ∙ x2 + y1 ∙ y2.
Задание 1. Реализуйте задачу «Штраф за левые повороты»
Задача 2 «Здесь будет город-сад». Жители одного дома города Х решили высадить у себя во дворе несколько деревьев. Так как жильцы не смогли договориться, как должны быть расположены посадки, то каждый посадил дерево в том месте двора, где ему захотелось. После проведения посадок полученный сад решили обнести забором. Но пока доски не привезли, деревья обвязали одной длинной веревкой.
Исходная информация: N – количество деревьев в саду, (xi, yi) – координаты деревьев, i=1,2, …, N. Так как были высажены молодые саженцы, то их толщиной можно пренебречь.
Требуется определить, к каким из посаженных деревьев надо привязать веревку так, чтобы все деревья оказались внутри обнесенной зоны, а длина веревки была минимальная.
Эта и подобные ей задачи сводятся к определению для заданного множества точек на плоскости выпуклой оболочки, то есть выпуклого многоугольника с вершинами в некоторых точках из заданного множества, охватывающего все его точки. В [2] приведено несколько вариантов решения такой задачи с учетом временных затрат на выполнение алгоритмов. Здесь мы рассмотрим способ, использующий свойства скалярного произведения векторов.
Будем строить выпуклую оболочку в порядке обхода участка по часовой стрелке. Найдем самую левую точку М0=(x0, y0), x0=min<xi>. Если таких точек несколько, то возьмем самую нижнюю из них. Эта точка наверняка принадлежит искомой выпуклой оболочке. Зададим первоначальный вектор a0 с началом в точке (x0, y0), параллельный оси Oy.
Следующей точкой оболочки будет такая точка М1, чтобы вектор a1 с началом в точке М0 и концом в точке М1 образовывал с первоначальным вектором a0 минимальный угол. Если таких точек несколько, то выбирается точка, расстояние до которой максимально.
Далее процесс продолжаем, то есть ищем точку М2 с минимальным углом между вектором a1 и вектором a2 с началом в точке М1 и концом в точке М2, затем точку М3 и т.д. Процесс прекращаем, когда дойдем до первой выбранной точки или количество точек в оболочке станет равно N.
Для определения угла между векторами используется скалярное произведение. Причем сам угол можно не вычислять, так как минимальному углу соответствует максимальный косинус угла.
Задание 2. Реализуйте задачу «Здесь будет город-сад»
Задача 3 «Заяц» [3]. Недалеко от города Х находится зоосад. Здешний житель, заяц, хаотично прыгая, оставил след в виде замкнутой самопересекающейся ломаной, охватывающей территорию его владения. Найти площадь минимального по площади выпуклого многоугольника, описанного вокруг этой территории.
В данной задаче необходимо не только найти выпуклую оболочку множества точек, но и вычислить площадь выпуклого многоугольника с заданным набором вершин.
Исходные данные: N – количество вершин выпуклого многоугольника, (xi, yi) – координаты вершин, i=1,2, …, N.
Требуется определить площадь выпуклого N-угольника.
Площадь N-угольника может быть вычислена как сумма площадей треугольников, из которых N-угольник составлен. Для нахождения площади треугольника используем векторное произведение. Длина векторного произведения векторов, как известно, равна удвоенной площади треугольника, построенного на этих векторах. Пусть вершины треугольника расположены в точках A=(x1, y1), B=(x2, y2), C=(x3, y3). Совместим начало координат с первой точкой. Векторное произведение равно
[AB × AC]= 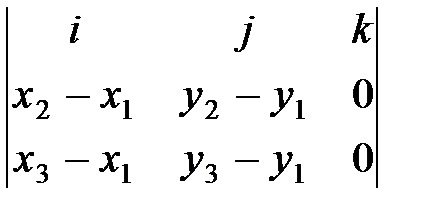
следовательно, площадь треугольника равна
Значение величины SABC может быть как положительным, так и отрицательным числом, так как оно зависит от взаимной ориентации векторов AB и AC, поэтому говорят, что площадь ориентированная.
| А1 |
| А2 |
| А3 |
| А4 |
| А5 |
Для нахождения площади N-угольника последний требуется разбить на треугольники и найти сумму ориентированных площадей этих треугольников. Разбиение N-угольника на треугольники можно провести так: зафиксировать одну из вершин N-угольника, например, первую A1=(x1, y1) и рассматривать все треугольники A1Ai Ai+1, i=2, 3,…, N-1.
Заметим, что аналогичным способом можно находить площадь произвольного многоугольника.
Использование свойства ориентации площади треугольника, вычисленной по векторному произведению, позволяет определить, является ли заданный многоугольник выпуклым. Для выпуклого многоугольника все треугольники, образованные тройками соседних вершин в порядке их обхода, имеют одну ориентацию. Поэтому проверка многоугольника на выпуклость может быть проведена с помощью последовательного сравнения знаков векторных произведений для всех пар соседних сторон многоугольника.
Задание 3. Реализуйте задачу «Заяц»
Задача 4 «Тигр в загоне». Недалеко от города Х находится заповедник, в котором обитают уссурийские тигры. Работники заповедника очень переживают, когда тигр покидает охраняемую зону. Программа охраны уссурийских тигров предусматривает снабжение каждого тигра ошейником с радиомаяком. Сигнал от тигриного радиомаяка поступает в центр охраны и позволяет определить местоположения тигра. Территория заповедника представляет собой произвольный многоугольник.
Исходные данные: N – количество вершин многоугольника, задающего заповедник, (xi, yi) – координаты его вершин, i=1,2, …, N. (X, Y) – координаты точки, в которой находится тигр.
Требуется определить, находится ли тигр на территории заповедника, или надо срочно снаряжать спасательную экспедицию.
| P |
| Q |
Очень часто при решении задач геометрического содержания требуется проверить, лежит ли заданная точка внутри или вне многоугольника. Таким способом можно решить, например, задачу о Бармаглоте, проверяя каждую точку Бармаглота относительно одеяла-многоугольника. Есть много способов проверки принадлежности точки многоугольнику, однако мы приведем здесь один из них, основанный на использовании произведения векторов.
Идея метода заключается в том, чтобы определить сумму углов, под которыми стороны многоугольника видны из проверяемой точки. Если точка лежит внутри многоугольника, то суммарный угол равен 2π (точка Р на рисунке), если же точка лежит вне многоугольника, то сумма углов не равна 2π (точка Q).
Таким образом, для решения надо перебрать в цикле последовательно все вершины многоугольника и найти сумму углов между векторами PAi и PAi+1, i=1,2, …, N. Не забудьте добавить угол между векторами PAN и PA1. Для определения величины угла между векторами нам потребуется формула скалярного произведения.
Так как стороны многоугольника должны рассматриваться последовательно, в порядке обхода вершин, то при нахождении суммарного угла следует учитывать взаимное расположение векторов. Угол, под которым сторона видна из исследуемой точки, может быть как положительным, так и отрицательным. Для определения знака угла воспользуемся векторным произведением. Знак векторного произведения и определит знак конкретного угла в общей сумме.
Задание 4. Реализуйте задачу «Тигр в загоне»
Задача 5 «Пересечение отрезков». Дано n отрезков. Реализовать программу, находящую все их пересечения между собой. Отобразить решение графически.
На плоскости заданы два отрезка a и b, a – точками A 1 (A 1 x,A 1 y) и A 2 (A 2 x,A 2 y), а b – точками B 1 (B 1 x,B 1 y) и B 2 (B 2 x,B 2 y). Найти и напечатать возможную точку их пересечения C(Cx,Cy). Рассмотрим первый отрезок a. Уравнение прямой, на которой он лежит можно записать так:
Здесь, A 1 x,A 1 y,A 2 x,A 2 y – константы, xa,ya – точки принадлежащие отрезку, при ta изменяющемся от 0 до 1. Аналогично для отрезка b:
Таким образом, приравнивая соответствующие координаты, получаем задачу нахождения параметров ta,tb, при которых бы выполнялись равенства:
После разрешения системы относительно ta,tb получаем:
А это есть система из двух линейных уравнений относительно ta,tb.
- ВПЧМВД С# 2 курс. Практикум по информатике рекомендовано в качестве учебного пособия
- Формирование задержки с помощью таймера
- Индивидуальное задание
- Напишите программу, которая рисует ряд окружностей заданного радиуса, расположенных по диагонали графического окна. Рассмотрите два варианта:
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 🎦 Видео
Видео:😱 Как сделать ANDROID приложение за 10 минут! Сможет каждый :3Скачать

ВПЧМВД С# 2 курс. Практикум по информатике рекомендовано в качестве учебного пособия
| Название | Практикум по информатике рекомендовано в качестве учебного пособия |
| Дата | 03.11.2021 |
| Размер | 1.13 Mb. |
| Формат файла |  |
| Имя файла | ВПЧМВД С# 2 курс.docx |
| Тип | Практикум #262499 |
| страница | 40 из 48 |
| Подборка по базе: Реферат по информатике.docx, Задание для лабораторного практикума.docx, Работа по информатике.docx, Контр. работа. Практикумы по психодиагностике.docx, Основы управленческой деятельности практикум.pdf, ЛБ по информатике куропаткин1.docx, экзаменационные вопросы по информатике.docx, Входная контрольная работа по информатике в 7 классе 4 варианта., Курсовая лабораторный практикум по фининсовому учету.docx, Общий псих практикум 3 семестр.docx Видео:Сколько стоит разработать мобильное приложение? Реальная стоимость разработки приложения.Скачать  Формирование задержки с помощью таймераГрафические конструкции иногда требуется рассматривать дина- мически в процессе их построения. Поэтому зачастую используется та- кая схема вывода графики:
Реализация задержки с помощью таймера возможна следующим способом: // Глобальное поле flag private bool flag = false; // Далее следует часть программы, // где необходимо организовать задержку // Устанавливаем flag в значение true flag = true; // Организуем бесконечный цикл // Выключаем таймер после выхода из цикла // Обработчик тика таймера private void timer1_Tick_1(object sender, EventArgs e) // Сбрасываем flag в значение false Идея данного подхода заключается в организации бесконечного цик- ла, который будет проверять значение некого флага. Однако значение фла- га может измениться при наступлении события Tick таймера, то есть через заданный в таймере промежуток времени. Однако бесконечный цикл, опи- санный выше, останется бесконечным, и программа просто зависнет. В чем же дело? Дело в том, что при такой организации цикла программа не мо- жет опросить очередь сообщений, в которое и будет поступать, в том чис- ле, и событие Tick от таймера. Тем самым мы не попадем никогда в обра- ботчик события timer1_Tick_1 . Чтобы решить данную проблему, надо в теле цикла написать Application.DoEvents() , что фактически будет за- ставлять приложение опрашивать очередь сообщений и в свою очередь приведет к срабатыванию обработчика событияtimer1_Tick_1. Перед выполнением индивидуального задания по лабораторной ра- боте разработайте приложение, строящее ряд увеличивающихся квадра- тов (рис. 14.2). Квадраты выводятся последовательно через одну секунду. Видео:1 2 4 сопряжение окружностейСкачать  Индивидуальное задание
по диагонали. Число окружностей задается при первом вызове рекур- сивного метода.
Цельлабораторнойработы: освоить основные алгоритмы сорти- ровки, написать программу с использованием этих алгоритмов.
Видео:C# .NET Windows Form | СОЗДАЁМ PAINT НА C#Скачать  Напишите программу, которая рисует ряд окружностей заданного радиуса, расположенных по диагонали графического окна. Рассмотрите два варианта:Видео:Как ПРАВИЛЬНО создать мобильное приложение в 2023 году | Шаг за шагомСкачать  Ваш ответВидео:Делаем свое приложение "Кубик" | MIT App Inventor 2Скачать  решение вопросаВидео:Я попробовал 50 NO CODE сервисов, вот лучшие из них!Скачать  Похожие вопросыПопулярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 🎦 ВидеоСоздай мобильное приложение без кодаСкачать  Уроки C# / Как сделать первое Windows приложениеСкачать  Приложения для Учёбы | Полезно!Скачать  Как создать Android игру за 10 минут на языке Python!Скачать  Glide: делаем мобильное приложение за часСкачать  Сколько стоит разработать мобильное приложение в 2022 году?Скачать  приложение рентгенСкачать  Приложение за пару секунд на JavaСкачать  ТОП 6 ПРИЛОЖЕНИЙ НА АНДРОИД ДЛЯ ПРОГРАММИСТОВСкачать  Андроид Студио эмулятор в отдельном окне 2. #ShortsСкачать  4 топовые платформы для разработки мобильных приложений без кодаСкачать  Революционный проект: Создаем приложение на Android Studio с помощью ChatGPT AIСкачать  Создаем свое ANDROID приложение на PYTHONСкачать  |




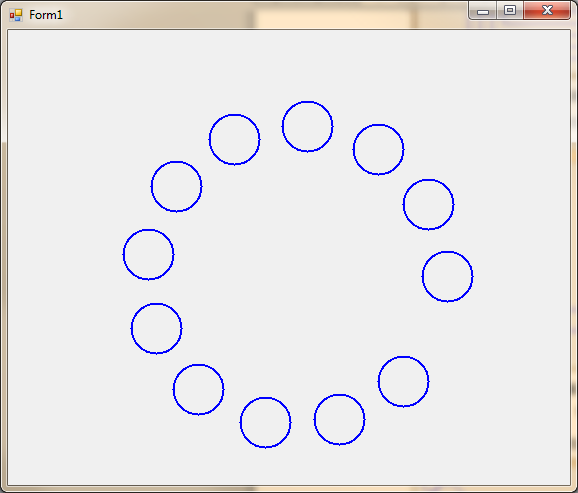









 Напишите приложение, которое строит ряд окружностей. Центр окружностей совпадает с центром экрана. Число окружностей за- дается при первом вызове рекурсивного метода.
Напишите приложение, которое строит ряд окружностей. Центр окружностей совпадает с центром экрана. Число окружностей за- дается при первом вызове рекурсивного метода.












