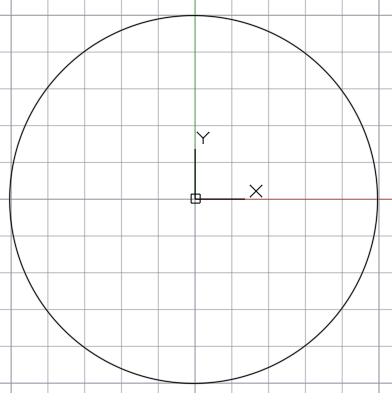
Окружность разделена на 12 равных дуг (6 видео)

Деление окружности на 12 равных частей

Итак, разделим окружность на 12 равных частей с помощью циркуля. Чертим циркулем окружность

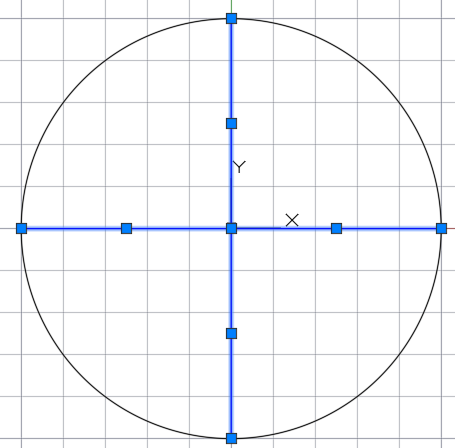
Чертим в окружности два взаимно перпендикулярных диаметра

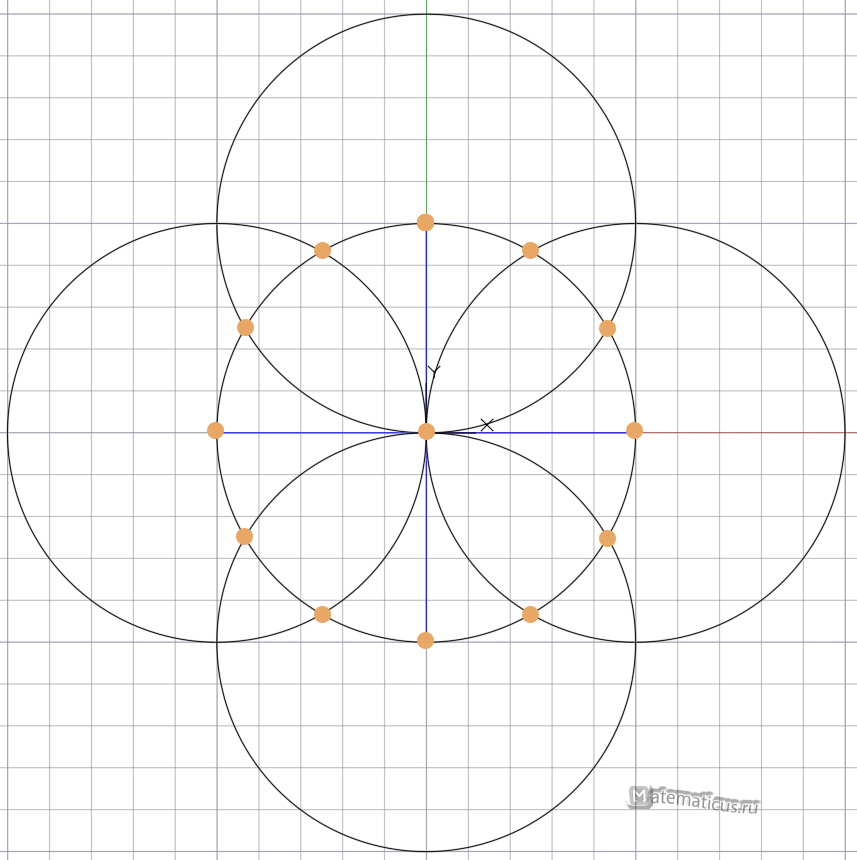
С помощью циркуля в точках окончания диаметров чертим четыре таких же окружности и отмечаем точки в областях пересечения новых окружностей с первоначальной.

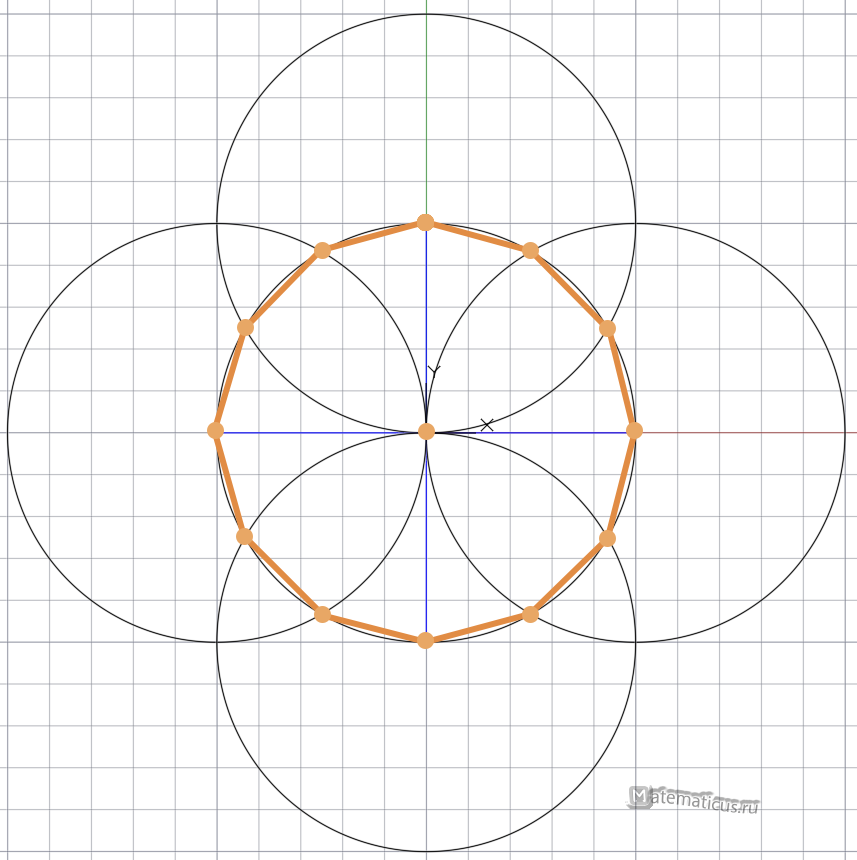
При помощи линейки последовательно соединяем точки друг с другом и получаем равносторонний двенадцатиугольник, то есть правильный двенадцатиугольник.

Затем с помощью линейки к центру первоначальной окружности проводим отрезки и тем самым делим окружность на 12 равных частей.

Содержание

Начертите окружность произвольного радиуса, разделите её на 12 равных дуг. Используя точки деления, постройте двенадцатиугольник, вписанный в окружность.
Ваш ответ
решение вопроса
Похожие вопросы
Деление круга на равные части
Деление круга на равные по площади части радиусами
Деление круга на равные по площади части параллельными хордами
Деление круга на равные части радиусами
Деление круга на равные части параллельными хордами
🎦 Видео

Видео:КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

Начертите окружность произвольного радиуса, разделите её на 12 равных дуг. Используя точки деления, постройте двенадцатиугольник, вписанный в окружность.

Видео:Деление окружности на 12 равных частейСкачать

Ваш ответ

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

решение вопроса

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Деление круга на равные части

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

Деление круга на равные по площади части радиусами

Деление круга на равные по площади части параллельными хордами

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:

Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

Определяем размер дуги сектора, перемножая радиус на угол в радианах

Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

Собственно и всё — мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.

По теореме Пифагора получаем следующую функцию

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

Итак, полное выражение

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

Таким образом мы можем приравнять

Что дает нам такое финальное уравнение

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.