Нахождение стороны bc треугольника (6 видео)

Все формулы для треугольника

Содержание

1. Как найти неизвестную сторону треугольника
2. Как узнать сторону прямоугольного треугольника
3. Формулы сторон равнобедренного треугольника
4. Найти длину высоты треугольника
Формулы треугольника
Виды треугольников
Свойства треугольника, применимые к любому треугольнику:
Признаки равенства треугольников
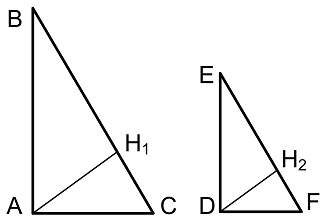
Подобные треугольники
Площадь треугольника
Стороны треугольника
Высота треугольника
Биссектрисы в треугольнике
Медиана в треугольнике
Описанная окружность
Вписанная окружность
Решение треугольников онлайн
Решение треугольника по трем сторонам
Решение треугольника по двум сторонам и углу между ними
Решение треугольника по стороне и любым двум углам
🎦 Видео

Видео:Нахождение стороны прямоугольного треугольникаСкачать

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

Видео:ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Видео:Уравнения стороны треугольника и медианыСкачать

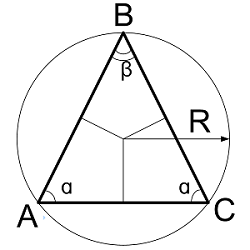
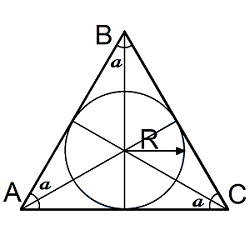
3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

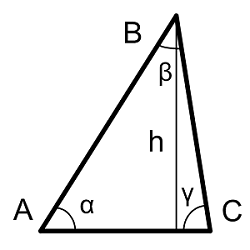
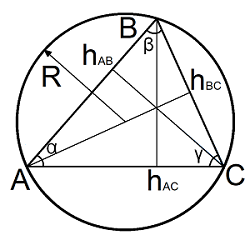
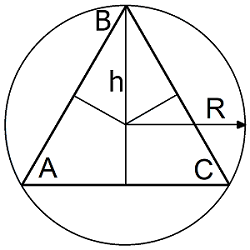
4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Формулы треугольника

Для расчёта всех основных параметров треугольника воспользуйтесь калькулятором.

Виды треугольников

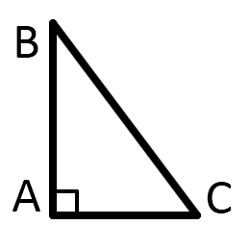
Остроугольный треугольник — это треугольник, в котором все три угла острые, т.е. меньше 90°.

Прямоугольный треугольник — это треугольник, содержащий прямой угол.
Две стороны, образующие прямой угол, называются катетами (АС и АВ), а сторона, противолежащая прямому углу, называется гипотенузой (ВС).

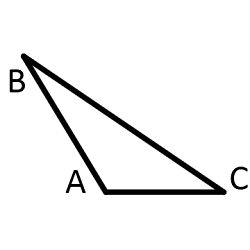
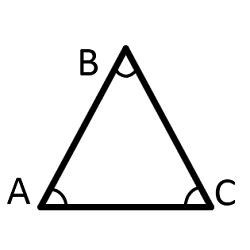
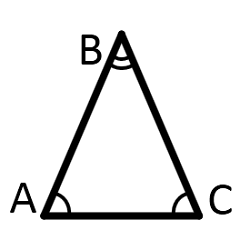
Тупоугольный треугольник — это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.(по числу равных сторон)

Равносторонний (правильный) треугольник — это треугольник, у которого все стороны и все углы равны (каждый угол равен 60°).

Равнобедренный тругольник — это треугольник, у которого два угла и две стороны равны.

Разносторонний треугольник — это треугольник, в котором все углы, а значит и все стороны попарно различны.

Свойства треугольника, применимые к любому треугольнику:

Против большей стороны лежит больший угол, и наоборот.
Против равных сторон лежат равные углы, и наоборот. (В частности, все углы в равностороннем треугольнике равны.)
Сумма углов треугольника равна 180° (Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60°).
Продолжая одну из сторон треугольника (AВ), получаем внешний угол Θ.
Любая сторона треугольника меньше суммы двух других сторон и больше их разности:

$$ AB BC — CA $$
$$ BC AB — CA $$
$$ CA AB — BC $$

Признаки равенства треугольников

Произвольные треугольники равны, если:

Три стороны одного треугольника равны трем сторонам другого треугольника (по трем сторонам).

AB = DE и BC = EF и AC = DF

Две стороны одного треугольника равны двум сторонам другого треугольника и углы между этими сторонами также равны (по двум сторонам и углу между ними).

AB = DE и BC = EF и ∠ABC = ∠DEF;

BC = EF и AC = DF и ∠BCA = ∠EFD;

AB = DE и AC = DF и ∠CAB = ∠FDE;

Три угла одного треугольника равны трем углам другого треугольника (по трем углам).

∠ABC = ∠DEF и ∠BCA = ∠EFD и ∠CAB = ∠FDE;

Два угла одного треугольника равны двум углам другого треугольника, и любая сторона первого треугольника равна соответствующей стороне другого треугольника.

∠ABC = ∠DEF и ∠BCA = ∠EFD;

∠BCA = ∠EFD и ∠CAB = ∠FDE;

∠CAB = ∠FDE и ∠ABC = ∠DEF;

AB = DE или BC = EF или AC = DF

Прямоугольные треугольники равны, если равны:

BC = EF и ∠ABC = ∠DEF

BC = EF и ∠BCA = ∠EFD;

Катет и противолежащий угол.

AB = DE и ∠BCA = ∠EFD

AC = DF и ∠ABC = ∠DEF

Катет и прилежащий угол.

AB = DE и ∠ABC = ∠DEF

AC = DF и ∠BCA = ∠EFD

AB = DE и AC = DF

Гипотенуза и катет.

AB = DE и BC = EF

AC = DF и BC = EF

Подобные треугольники

Два треугольника являются подобными, если углы одного треугольника равны, углам тругого треугольника, а стороны подобны

Признаки подобия треугольников

Два угла одного треугольника равны двум углам другого треугольника.
Две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны.
Три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.

Свойства подобных треугольников.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия (K_{подобия}) $$ <S_over S_> = К_^2 $$
Отношение периметров и длин биссектрис, медиан, высот, серединных перпендикуляров равно коэффициенту подобия. т.е. в подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.

Подобие в прямоугольных треугольниках.

Треугольники, образованные высотой, опущенной из прямого угла, являются подобными друг другу
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.

Площадь треугольника

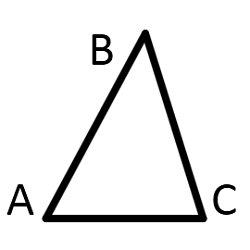
Где:	AB,BC,AC – стороны треугольника
h – высота треугольника
α, β, γ– углы треугольника
P – полупериметр
AC – основание треугольника

Площадь произвольного треугольника

Площадь треугольника по формуле Герона

Площадь треугольника по углу и двум сторонам

$$ S = * AB * AC * sin(α) $$ $$ S = * AB * BC * sin(β) $$ $$ S = * AC * BC * sin(γ) $$

Площадь треугольника по двум углам и стороне

Площадь прямоугольного треугольника по катетам

Где:	AB,AC – катеты треугольника

$$ S = * AB * AC $$

Площадь равнобедренного треугольника

Где:	AB,BC – равные стороны треугольника
AC – основание треугольника

$$ S = * sqrt $$

Площадь равностороннего треугольника

Где:	AB,BC,AC – равные стороны треугольника
h – высота треугольника

$$ S = <sqrtover 4> * AB^2 $$ $$ S = <h^2 over sqrt> $$

Стороны треугольника

Где:	AB,BC,AC – стороны треугольника
h – высота треугольника
α, β, γ– углы треугольника
P – полупериметр
AC – основание треугольника

Сторона треугольника по двум сторонам и углу

Сторона треугольника по стороне и двум углам

Сторона прямоугольного треугольника

Где:	AB,AC – катеты треугольника
BC – гипотенуза треугольника

$$ AC = BC * cos(β) = BC * sin(α) = AB * tg(α) $$ $$ AB = BC * cos(α) = BC * sin(β) = AC * tg(β) $$ $$ BC = = $$ $$ BC = = $$

Сторона прямоугольного треугольника по теореме Пифагора.

Сторона равнобедренного треугольника

Где:	AB,BC – равные стороны треугольника
AC – основание треугольника

$$ AC = 2 * AB * sin() = AB * sqrt $$ $$ AC = 2 * AB * cos(α) $$ $$ AB = = <AC over sqrt> $$ $$ AB = $$

Высота треугольника

Высота – это перпендикуляр, выходящий из любой вершины треугольника, к противоположной стороне или её продолжению для треугольника с тупым углом. Высоты треугольника пересекаются в одной точке

Где:	AB,BC,AC – стороны треугольника
h – высота треугольника
P – полупериметр $$ P = $$
α, β, γ – углы треугольника
R — радиус описанной окружности
S — площадь треугольника

Высота на сторону АС, h_AC

Высота на сторону AB, h_AB

Высота на сторону BC, h_BC

Формула длины высоты через сторону и угол

Высота на сторону АС, h_AC

$$ h_ = AB * sin(α) = BC * sin(γ) $$

Высота на сторону AB, h_AB

$$ h_ = BC * sin(β) = AC * sin(α) $$

Высота на сторону BC, h_BC

$$ h_ = AC * sin(γ) = AB * sin(β) $$

Формула длины высоты через сторону и площадь

Высота на сторону АС, h_AC

Высота на сторону AB, h_AB

Высота на сторону BC, h_BC

Формула длины высоты через стороны и радиус

Высота на сторону АС, h_AC

Высота на сторону AB, h_AB

Высота на сторону BC, h_BC

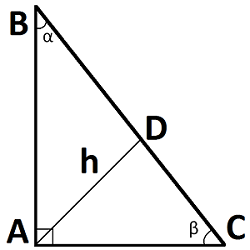
Формулы высоты из прямого угла в прямоугольном треугольнике

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.

Где:	AB,AC – катеты треугольника
BC – гипотенуза треугольника
BD, DC – отрезки полученные от деления гипотенузы, высотой
α, β– углы треугольника

Формула длины высоты через гипотенузу и острые углы

$$ h = BC * sin(α) * cos(α) = BC * sin(β) * cos(β) $$

Формула длины высоты через катет и угол

$$ h = AB * sin(α) = AC * sin(β) $$

Формула длины высоты через составные отрезки гипотенузы

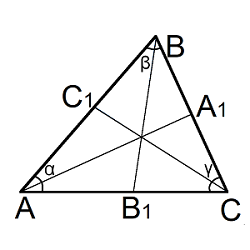
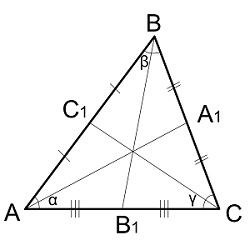
Биссектрисы в треугольнике

Биссектриса – это отрезок, который делит угол пополам из которого выходит. Точка пересечения всех трех биссектрис треугольника совпадает с центром вписанной окружности.

Где:	AB,BC,AC – стороны треугольника
AA₁,BB₁,CC₁ — биссектрисы в треугольнике
α, β, γ– углы треугольника
P – полупериметр $$ P = $$

Длина биссектрисы через две стороны и угол

Длина биссектрисы через полупериметр и стороны

Длина биссектрисы через три стороны

Длина биссектрисы через стороны и отрезки, на которые делит биссектриса

Формула длины биссектрис в прямоугольном треугольнике

Где:	AB,AC – катеты треугольника
BC – гипотенуза треугольника
β, γ– острые углы треугольника

Длина биссектрисы из прямого угла, через катеты.

Длина биссектрисы из прямого угла, через гипотенузу и угол

Длина биссектрисы через катет и угол

Длина биссектрисы через катет и гипотенузу

Длина биссектрисы равнобедренного треугольника

Где:	AB,BC – равные стороны треугольника
AC – основание треугольника
α – равные углы при основании треугольника
β – угол образованный равными сторонами треугольника

Длина биссектрисы через стороны и угол, равнобедренного треугольника

$$ BB_1 = AB * sin(α) = * tg(α) = AB * cos() $$ $$ BB_1 = AB * sqrt <over 2> $$

Длина биссектрисы через стороны, равнобедренного треугольника

Длина биссектрисы равностороннего треугольника

Где:	AB,BC,AC – равные стороны треугольника

$$ BB_1 = <AB * sqrtover 2> $$

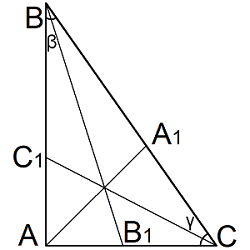
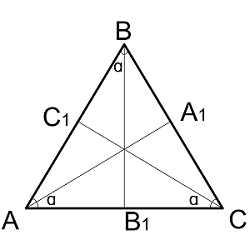
Медиана в треугольнике

Медиана – это отрезок, который выходит из вершины и делит противоположную сторону пополам. Медиана делит треугольник на два равных по площади треугольника.

Где:	AB,BC,AC – стороны треугольника
AA₁,BB₁,CC₁ — медианы в треугольнике
α, β, γ– углы треугольника

Длина медианы через три стороны

Длина медианы через две стороны и угол между ними

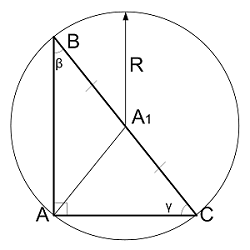
Длина медианы в прямоугольном треугольнике, выходящая из прямого угла.

Где:	AB,AC – катеты треугольника
BC – гипотенуза треугольника
AA₁,BB₁,CC₁ — медианы в треугольнике
β, γ– острые углы треугольника

Длина медианы в прямоугольном треугольнике, выходящая из прямого угла, равна радиусу описанной окружности, а середина гипотенузы является центром описанной окружности

Длина медианы через катеты

Длина медианы через катет и острый угол

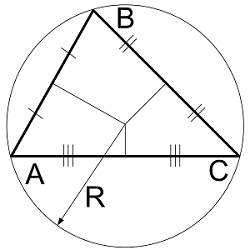
Описанная окружность

Радиус описанной окружности произвольного треугольника по сторонам

Где:	AB,BC,AC – стороны треугольника
P – полупериметр $$ P = $$
R — радиус описанной окружности

$$ R = <AB * BC * CA over 4 * sqrt

> $$

Радиус описанной окружности равностороннего треугольника по стороне или высоте

Где:	AB,BC,AC – равные стороны треугольника
h – высота треугольника
R — радиус описанной окружности

$$ R = <AB over sqrt> $$ $$ R = $$

Радиус описанной окружности равнобедренного треугольника по сторонам

Где:	AB,BC – равные стороны треугольника
AC – основание треугольника
h – высота треугольника
R — радиус описанной окружности

$$ R = <AB^2 over sqrt> $$

Радиус описанной окружности прямоугольного треугольника по катетам

Где:	AB,AC – катеты треугольника
BC – гипотенуза треугольника
R — радиус описанной окружности

$$ R = * sqrt = $$

Длина окружности, L

Площадь окружности, S

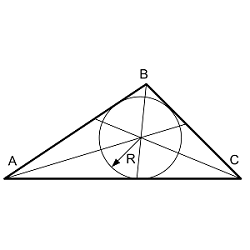
Вписанная окружность

Радиус вписанной окружности произвольного треугольника по сторонам

Где:	AB,BC,AC – стороны треугольника
P – полупериметр $$ P = $$
R — радиус вписанной окружности

$$ R = sqrt <

over P> $$

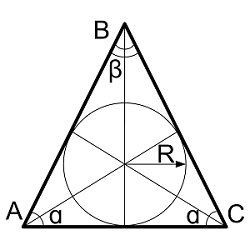
Радиус вписанной окружности в равносторонний треугольник

Где:	AB,BC,AC – равные стороны треугольника
R — радиус вписанной окружности

$$ R = <AB over 2 * sqrt> $$

Радиус вписанной окружности равнобедренного треугольник

Где:	AB,BC – равные стороны треугольника
AC – основание треугольника
R — радиус вписанной окружности
h – высота треугольника
α – угол при основании треугольника

$$ R = * sqrt <> $$ $$ R = AB * = AB * cos(α) * tan() $$ $$ R = * = * tan() $$ $$ R = <AC * h over AC + sqrt> $$ $$ R = <h * sqrtover AB + sqrt> $$

Радиус вписанной окружности в прямоугольном треугольнике

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

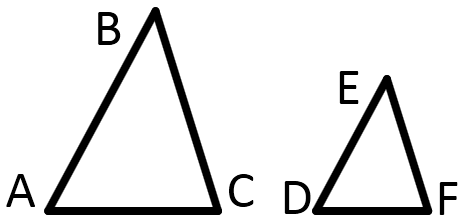
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это: