Геометрия | 5 — 9 классы
На высоте AH равнобедренного треугольника ABC с прямым углом А взята точка О.
Докажите что треугольнике AOB и AOC равны.
В равнобедренном прямоугольном треугольнике острые углы равны 45 градусов.
Высота, проведенная к гипотренузе, является еще и медианой и биссектрисой.
Угол А делится на два равных угла по 45 градусов.
Гипотенуза делится на ВН = НС
Углы при пересечении высоты с гипотенузой прямые.
По условию задачи АВ = АС.
Высота АН — общая для обоих треугольников.
Треугольники АВН и АСН равны по равенству как всех трех углов, так и равенству трех их сторон.
- На медиане CM равнобедренного треугольника ABC с основанием AB взята точка O?
- На медиане CM равнобедренного треугольника ABC с основанием AB взята точка O?
- Биссектриса AM иCK углов при основании AC равнобедренного треугольника ABC пересекаются в точке O?
- Биссектрисы am и ck углов при основании АС равнобедренного треугольника ABC пересекаются в точке O Докажите что треугольник aoc равнобедренный?
- В треугольнике ABC углы BAC и BCA равны, биссектрисы AA1 и CC1 пересекаются в точке O?
- Биссектрисы AM и CK углов при основании AC равнобедренного треугольника ABC пересекаются в точке О?
- На высоте AH равнобедренного треугольника ABC с прямым углом А взята точка О?
- Точка О лежит внутри треугольника ABC так, что треугольник AOB равен треугольнику COB, AO = OC, угол AOC = 140 (градусов)?
- На высоте AH равнобедренного треугольника ABC с прямым углом А взята точка О?
- Углы AOB и AOC равны , а точки B , O и C лежат на одной прямой?
- 16. Планиметрия
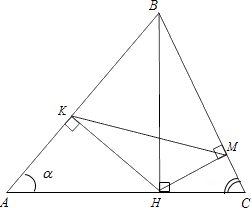
- Задание 16. Математика ЕГЭ. В равнобедренном треугольнике ABC, где угол B – тупой, на продолжение стороны BC опущена высота AH. ИЗ точки H на стороны AB и AC опущены перпендикуляры HK и HM соответственно.
- 🔍 Видео
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

На медиане CM равнобедренного треугольника ABC с основанием AB взята точка O?
На медиане CM равнобедренного треугольника ABC с основанием AB взята точка O.
Докажите, что треугольник AOB равнобедренный.
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

На медиане CM равнобедренного треугольника ABC с основанием AB взята точка O?
На медиане CM равнобедренного треугольника ABC с основанием AB взята точка O.
Докажите, что треугольник AOB равнобедренный.
Видео:№263. Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольникаСкачать

Биссектриса AM иCK углов при основании AC равнобедренного треугольника ABC пересекаются в точке O?
Биссектриса AM иCK углов при основании AC равнобедренного треугольника ABC пересекаются в точке O.
Докажите что AOC равнобедренный.
Видео:№265. В равнобедренном треугольнике ABC с основанием АС проведены биссектриса AF и высота АН.Скачать

Биссектрисы am и ck углов при основании АС равнобедренного треугольника ABC пересекаются в точке O Докажите что треугольник aoc равнобедренный?
Биссектрисы am и ck углов при основании АС равнобедренного треугольника ABC пересекаются в точке O Докажите что треугольник aoc равнобедренный.
Видео:№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

В треугольнике ABC углы BAC и BCA равны, биссектрисы AA1 и CC1 пересекаются в точке O?
В треугольнике ABC углы BAC и BCA равны, биссектрисы AA1 и CC1 пересекаются в точке O.
Докажите, что треугольник AOC — равнобедренный.
Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Биссектрисы AM и CK углов при основании AC равнобедренного треугольника ABC пересекаются в точке О?
Биссектрисы AM и CK углов при основании AC равнобедренного треугольника ABC пересекаются в точке О.
Докажите что угол AOC — равнобедренный.
Видео:ВЫСОТА через СИНУС / равнобедренный треугольник / #планиметрия #27327Скачать

На высоте AH равнобедренного треугольника ABC с прямым углом А взята точка О?
На высоте AH равнобедренного треугольника ABC с прямым углом А взята точка О.
Докажите что треугольнике AOB и AOC равны!
С решением , чтоб понял !
Видео:№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

Точка О лежит внутри треугольника ABC так, что треугольник AOB равен треугольнику COB, AO = OC, угол AOC = 140 (градусов)?
Точка О лежит внутри треугольника ABC так, что треугольник AOB равен треугольнику COB, AO = OC, угол AOC = 140 (градусов).
Докажите, что луч BO является биссектрисой угла ABC.
Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

На высоте AH равнобедренного треугольника ABC с прямым углом А взята точка О?
На высоте AH равнобедренного треугольника ABC с прямым углом А взята точка О.
Докажите что треугольники AOB и AOC равны.
Видео:№261. Докажите, что в равнобедренном треугольнике высоты, проведенные из вершин основания, равны.Скачать

Углы AOB и AOC равны , а точки B , O и C лежат на одной прямой?
Углы AOB и AOC равны , а точки B , O и C лежат на одной прямой.
Докажите , что углы AOB и AOC прямые.
Вы находитесь на странице вопроса На высоте AH равнобедренного треугольника ABC с прямым углом А взята точка О? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Решение — в приложении.
Сумма внутреннего и внешнего углов равна 180° Находим внутренний угол при вершине b (т. Е. ∠abc) : 180 — 140 = 40° Поскольку треугольник abc — равнобедренный, следовательно углы при основании равны, следовательно∠abc = ∠acb = 40°.
Tgα = ВД(высоты) / 0, 5 * АС⇒10 / 7 = ВД / 14 ВД(высота) = 10 * 14 / 7 = 20⇒Sавс = 1 / 2 * 28 * 20 = 280.
1) 6 : 2 = 3 см — середина АВ и середина СD , так как они равны. 6 см + 3 см + 3 см = 12 см Ответ : 12 см 2) Не знаю как решать , извини. 3) Возьмем АВ за х AM = MB = x 2 Тогда MN = BN = MB 2 = x 4 AM : MN = x 2 : x 4 = 2 : 1 BN : AM = x ..
SΔ = (a * ha) / 2 SΔ = (14 * 6) / 2 = 42 см².
По твоему чертежу, но без окружности : А 0 — центр окружности I А0 — радиус I 0В — радиус I 0С — радиус I0___________C ∠А0С = ∠В0С = 90° I Соедини· А и· С I Получим равнобедренныйΔ А0С I А0 = 0С (это радиусы) I В равнобедренномΔ углы при основании B ..
1)х + х + 160 = 180 2х = 20 х = 10 2)160 + 10 = 170.
Так как треугольник авс равнобедренный ав = вс то и ам = ск тогда треугольник вмк равнобедренный.
Дано : угол АВ, угол АD = 80градусов, угол ВD, угол AC = углуCB (это равенствопоказывает то, что С — биссектриса АВ), уголAD = углуDC. Найти : уголBD Решение : 1) уголAD× 2 = углуAC уголAC = углуCB 80× 2 = 160 — угол CB 2) уголDC + уголCB = углуBD 8..
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

16. Планиметрия
Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
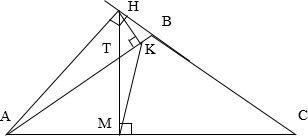
В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
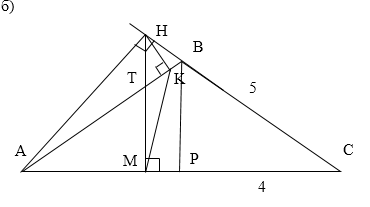
б) Найдите MK, если AB=5, AC=8.
Пусть $angle BAC=angle BCA=alpha .$ Тогда $angle ABC=180^-2alpha .$
$angle HBA=180^-180^+2alpha =2alpha $ как смежный с $angle ABC.$
Так как треугольник $AHB$ — прямоугольный, то $angle HAB=90^-2alpha .$
$angle HAC=angle HAB+angle BAC=90^-alpha .$
Так как треугольник $AHM$ — прямоугольный, то $angle AHM=90^-90^+alpha =alpha .$
Аналогично из прямоугольго треугольника $HKB$ получаем, что $angle BHK=90^-2alpha .$
Рассмотрим $angle AHB=90^=angle AHM+angle THK+angle BHK=alpha +angle THK+90^-2alpha Rightarrow angle THK=alpha .$
В треугольниках $ATM$ и $HTK$ $angle TAM=angle THK$ по доказанному, $angle AMT=angle HKT=90^$ по условию. Значит, данные треугольники подобны по призкаку подобия по 2 углам. Следовательно,
$displaystyle frac=displaystyle fracRightarrow displaystyle frac=displaystyle frac.$
В треугольнике $ATH$ и $MTK$ $angle ATH=angle MTK$ как вертикальные, $displaystyle frac=displaystyle frac$ по доказанномую Значит, данные треугольники подобны по 2 пропорциональнымсторонам и углу между ними. Тогда, $angle AHT=angle TKM=alpha .$
Получили, что в треугольнике $AKM$ углы при стороне $AK$ равны, значит, треугольник — равнобедренный и $AM=KM.$
Проведем прямую $BP//HM.$ В равнобедренном треугольнике $ABC$ отрезок $BP$ будет являться высотой и медианой, поэтому $PC=4.$ По теорем е Пифагора $BP^=sqrt<BC^-PC^>=3.$
Прямая $BP$ отсекает от треугольника $HCM$ подобные ему треугольник $BCP,$ поэтому $displaystyle frac=displaystyle frac,$
$displaystyle frac=displaystyle fracRightarrow HC=displaystyle fracCM.$
Обозначим $CM=x,$ тогда $HC=displaystyle fracx,$ $BH=displaystyle fracx-5,$ $AM=8-x.$
Из треугольника $ABH$ по теореме Пифагора $AH^=AB^-BH^=25-(displaystyle fracx-5)^=displaystyle fracx-displaystyle fracx^.$
Аналогично из треугольника $AHC$ $AC^=AH^+HC^$
$64=displaystyle fracx-displaystyle fracx^+displaystyle fracx^$
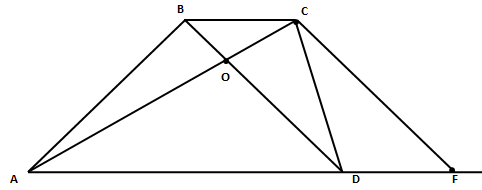
Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10.
а) Докажите, что диагонали перпендикулярны.
б) Найдите высоту трапеции.
а) Проведем прямую CF//BD, тогда BCFD – параллелограмм и BC = DF, CF = BD.
В треугольнике ACF AC = 8, CF = 6, AF = AD + DF = 10.
Если диагонали перпендикулярны, то треугольник ACF – прямоугольный и выполняется теорема Пифагора:
Значит, угол между диагоналями равен 90⁰.
б) $S_=displaystyle fraccdot h=5h,$ , где h – длинна высоты.
С другой стороны $S_=displaystyle fraccdot BDcdot ACcdot sin 90^=24$
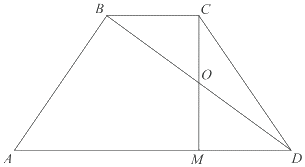
Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции.
а) Доказать, что M делит AD в отношении 2:1.
б) Найдите расстояние от точки C до середины BD, если AD = 18, $AC=4sqrt.$.
а) Поскольку ABCD — равнобедренная трапеция, то
$MD=displaystyle frac=displaystyle frac=BC$
Тогда $AM=2BC$. Следовательно, $displaystyle frac=displaystyle frac$
Треугольник AMC прямоугольный. В нем $AM=displaystyle fracAD=12$ по доказанному в пункте а) и $AC=4sqrt$ по условию.
По теореме Пифагора $CM^+AM^=AC^$ , откуда $CM=8$ .
Треугольники BCO и MOD равны по катету и острому углу (BC=MD по доказанному в пункте а) , углы CBO и ADO равны как накрест лежащие). Тогда BO = OD и СO = OM как соответственные элементы равных треугольников. Значит, СO — искомое расстояние.
В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.
а) Обозначим $angle BAC=alpha .$. Треугольники AKH, CMH, ABH и BKH – прямоугольные. Тогда $angle KHA=angle ABH=90^-alpha .$. Аналогично $angle KHB=90^-(90^-alpha )=alpha .$. В четырехугольнике BKHM $angle BKH+angle BMH=90^+90^=180^,$, значит, вокруг этого четырехугольника можно описать окружность. Углы $angle KHB=angle KMB=alpha $ как опирающиеся на одну и ту же хорду.
В треугольниках ABC и MKB $angle KMB=angle BAC,angle ABC$ — совпадающий. Значит, они подобны по признаку подобия по 2 углам.
б) Обозначим k – коэффициент подобия треугольников ABC и MKB (k
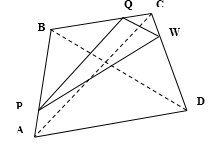
Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=1:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12, угол PWQ — острый.
а) Докажите, что треугольник PQW — прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
а) По теореме синусов из треугольника $PQW:$
$sin angle PWQ=displaystyle frac,sin angle QPW=displaystyle frac.$
Заметим, что $sin ^angle PWQ+sin ^angle QPW=displaystyle frac+displaystyle frac=1.$
$sin ^angle QPW=cos ^angle PWQ,$
$sin angle QPW=cos angle PWQ,$
так как угол $QWP$ — острый. Тогда $angle QPW+angle PWQ=90^$ и треугольник $PQW$ — прямоугольный.
б) Треугольник $PBQ$ и $ABC$ подобные по двум стронам и углу между ими ($angle B$ — общий, $displaystyle frac=displaystyle frac=displaystyle frac).$ Значит, $ACparallel PQ$ и $AC=displaystyle fracPQ=20.$
Аналогично, из подобия треугольников $QCW$ и $BCQ$ получаем, что $BDparallel QW$ и $BD=5QN=60$
Угол между прямыми $BD$ и $AC$ равен углу между прямыми $PQ$ и $QW,$ поэтому
$S_=displaystyle fracBDcdot ACcdot sin 90^=displaystyle frac60cdot 20=600.$
Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Задание 16. Математика ЕГЭ. В равнобедренном треугольнике ABC, где угол B – тупой, на продолжение стороны BC опущена высота AH. ИЗ точки H на стороны AB и AC опущены перпендикуляры HK и HM соответственно.
Задание.
В равнобедренном треугольнике ABC, где угол B – тупой, на продолжение стороны BC опущена высота AH. ИЗ точки H на стороны AB и AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что AM = MK.
б) Найдите MK, если AB = 13, AC = 24.
Решение:
а) Докажите, что AM = MK.
Так как, угол AKH = 90 0 , угол AMH = 90 0 , тогда отрезок AH виден из точек K и M под углом 90 0 . Поэтому точки A, M, K и H лежат на окружности, диаметром которой является отрезок AH (см. рис.1).
Угол AKM — вписанный в окружность угол, который опирается на дугу AM. Угол AHM — вписанный в окружность угол, который опирается на дугу AM. Следовательно, угол AKM равен углу AHM. Т.е.
Треугольник ΔAHC – прямоугольный, тогда
Треугольник ΔAHM – прямоугольный, тогда
Из (1) и (2) равенства имеем, что
Так как треугольник ΔABC – равнобедренный (AB = BC), то
Тогда в треугольнике ΔAKM:
Получаем, что треугольник ΔAKM – равнобедренный и AM = MK.
б) Найдите MK, если AB = 13, AC = 24.
Рассмотрим треугольник ΔAMH – прямоугольный, угол AHM = α, MK = AM
Рассмотрим треугольник ΔABP – прямоугольный:
BP 2 = AB 2 – AP 2
BP 2 = 13 2 – 12 2 = 25
Найдем площадь треугольника ΔABC:
С другой стороны, площадь треугольника ΔABC можно найти
Тогда, AH = 2· SABC/BC
AH = (2·60)/13 = 120/13
Подставим полученные значения в равенство (1), получаем:
🔍 Видео
Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

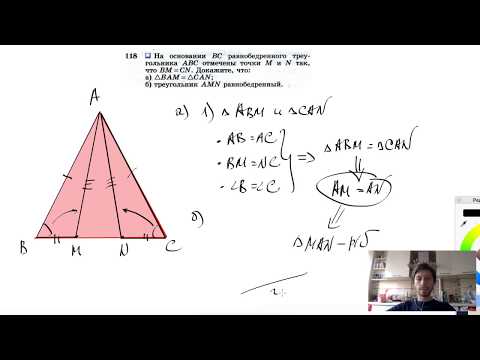
№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать
Высота, биссектриса, медиана. 7 класс.Скачать

Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Задание 6 ЕГЭ #156Скачать

№488. Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см;Скачать

Формулы равностороннего треугольника #shortsСкачать

Геометрия Высота равнобедренного треугольника, проведенная к основанию, равна h, а угол при вершинеСкачать