На рисунке изображена прямая а касающаяся окружности

Упражнения №№ 134-136. Самостоятельная работа по математике в 6 классе «Окружность и круг» для УМК Мерзляк с ОТВЕТАМИ. Цитаты из пособия «Математика 6 класс. Дидактические материалы / Мерзляк и др.» использованы в учебных целях. СР-23 Окружность и круг. Упражнения используются в комплекте с учебником «Математика 6 класс» авторов: Мерзляк, Полонский, Якир.

Математика 6 класс (Мерзляк)
Самостоятельная работа № 23
(упражнения №№ 134-136)

Тема: Окружность и круг

СР-23. Вариант 1

СР-23. Вариант 2

СР-23. Вариант 3

СР-23. Вариант 4

ОТВЕТЫ на самостоятельную работу
СР-23 Окружность и круг:

Ответы на Вариант 1

№ 134. Укажите центр, радиус, хорду и диаметр окружности, изображённой на рисунке 1. Сколько радиусов изображено на этом рисунке?
ОТВЕТ: Е — центр окружности, АЕ, ЕС, ЕD — радиусы, АВ, АС — хорды, АС — диаметр. Изображено 3 радиуса.

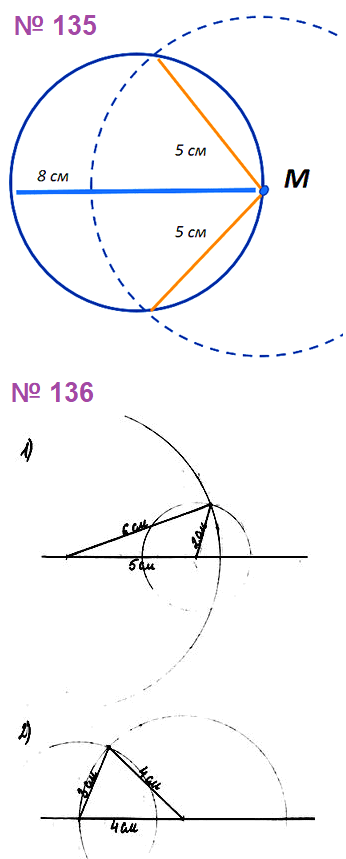
№ 135. Начертите окружность, диаметр которой равен 8 см. Отметьте на окружности точку М. Найдите на окружности точки, удалённые от точки М на 5 см.

№ 136. С помощью циркуля и линейки постройте треугольник со сторонами: 1) 5 см, 2 см и 6 см; 2) 4 см, 4 см и 3 см.

Ответы на Вариант 2

№ 134. Укажите центр, радиус, хорду и диаметр окружности, изображённой на рисунке 13. Сколько радиусов изображено на этом рисунке?
ОТВЕТ: С — центр окружности, АС, DС, FC — радиусы, АF, АB — хорды, АF — диаметр, Изображено 3 радиуса.

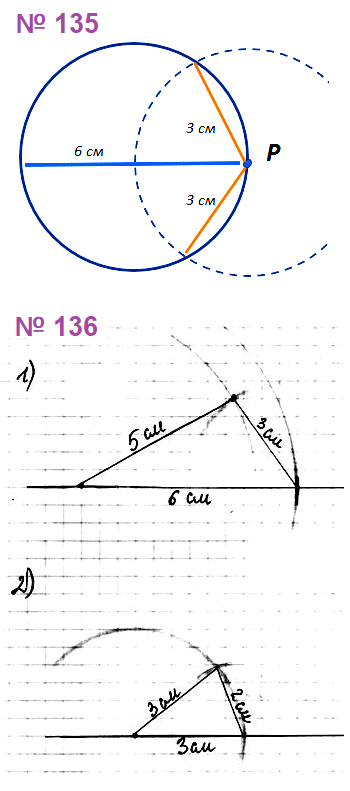
№ 135. Начертите окружность, диаметр которой равен 6 см. Отметьте на окружности точку Р. Найдите на окружности точки, удалённые от точки Р на 3 см.

№ 136. С помощью циркуля и линейки постройте треугольник со сторонами: 1) 5 см, 3 см и 6 см; 2) 3 см, 3 см и 2 см.

Ответы на Вариант 3

№ 134. Укажите на рисунке 25 центр, радиус, хорду и диаметр окружности. Сколько радиусов изображено на этом рисунке?
ОТВЕТ: К — центр окружности, АК, СК, BK — радиусы, АC, BC — хорды, АC — диаметр, Изображено 3 радиуса.

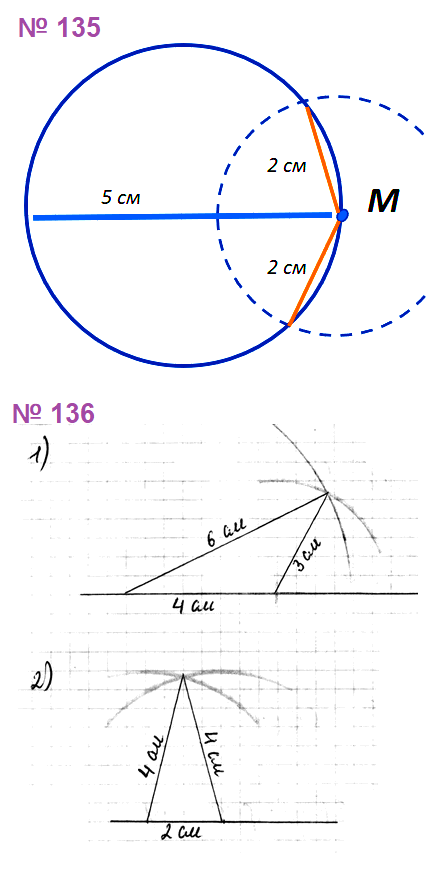
№ 135. Начертите окружность, диаметр которой равен 5 см. Отметьте на окружности точку М. Найдите на окружности точки, удалённые от точки М на 2 см.

№ 136. С помощью циркуля и линейки постройте треугольник со сторонами: 1) 4 см, 6 см и 3 см; 2) 4 см, 4 см и 2 см.

Ответы на Вариант 4

№ 134. Укажите центр, радиус, хорду и диаметр окружности, изображённой на рисунке 37. Сколько радиусов изображено на этом рисунке?
ОТВЕТ: F — центр окружности, CF, КF, BF — радиусы, АM, CK — хорды, CK — диаметр, Изображено 3 радиуса.

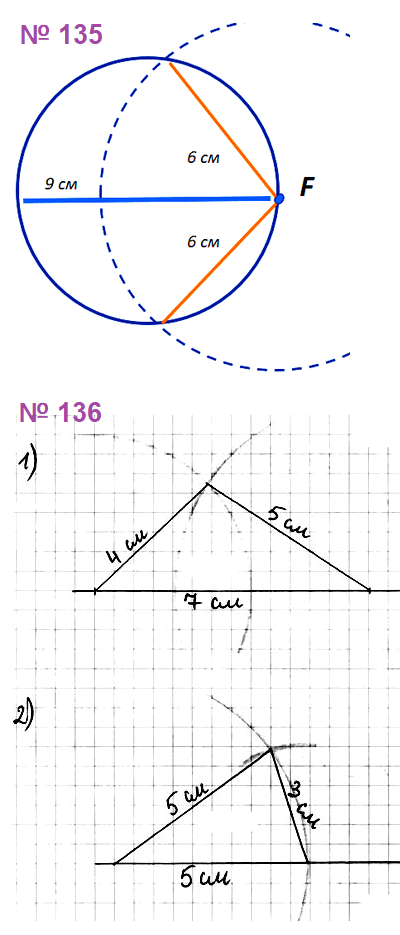
№ 135. Начертите окружность, диаметр которой равен 9 см. Отметьте на окружности точку F. Найдите на окружности точки, удалённые от точки F на 6 см.

№ 136. С помощью циркуля и линейки постройте треугольник со сторонами: 1) 4 см, 7 см и 5 см; 2) 5 см, 5 см и 3 см.

Вы смотрели «СР-23 Окружность и круг». Цитаты самостоятельных работ из пособия для учащихся «Математика 6 класс. Дидактические материалы / Мерзляк и др.», которое используется в комплекте с учебником «Математика 6 класс» авторов: Мерзляк, Полонский, Якир.

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Задача 7 ЕГЭ по математике. Урок 15.Скачать

Предметы

Видео:9 вариант ЕГЭ Ященко 2024 математика профильный уровеньСкачать

Новые работы

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Найти контрольную:

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Авторы работ и УМК

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Предметы

Видео:Все Задания 8 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать

Важные страницы

Соглашение о конфиденциальности

(с) 2021. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru

Видео:Задача 7 ЕГЭ по математикеСкачать

Популярное

Видео:Уравнение окружности (1)Скачать

Предупреждение

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Видео:10 вариант ЕГЭ Ященко 2024 математика профильный уровеньСкачать

Варианты МА2190301-МА2190304 ОГЭ 2022 математика 9 класс статград с ответами

ПОДЕЛИТЬСЯ

Тренировочная работа №3 пробный ОГЭ 2022 статград по математике 9 класс, тренировочные варианты МА2190301, МА2190302, МА2190303, МА2190304 с ответами и решением, официальная дата проведения работы 20 января 2022 года.

Скачать варианты МА2190301-МА2190302

Скачать варианты МА2190303-МА2190304

Скачать решения и ответы на все задания

Варианты МА2190301 МА2190302 статград ОГЭ 2022 по математике 9 класс:

Варианты МА2190303 МА2190304:

Сложные задания с 1 варианта:

Хозяин дачного участка строит баню с парным отделением. Парнóе отделение имеет следующие размеры: длина — 3,5 м, ширина — 2,2 м, высота — 2 м. Окон в парнóм отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма — 1,8 м. Для прогрева парнóго отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей. Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6500 руб.

1)Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наименьшим для отопления помещений. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.

Правильный ответ: 132

2)Найдите суммарную площадь стен парнóго отделения строящейся бани (без площади двери). Ответ дайте в квадратных метрах.

Правильный ответ: 21,7

3)Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 1000 рублей?

Правильный ответ: 22500

4)На электрическую печь сделали скидку 15 %. Сколько рублей стала стоить печь без учёта установки и доставки?

Правильный ответ: 12750

5)Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рис. 2. Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печи по дуге окружности с центром в середине нижней части кожуха (рис. 2). Для установки печи хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.

Правильный ответ: 55

10)В фирме такси в данный момент свободно 20 машин: 3 чёрные, 3 жёлтые и 14 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.

Правильный ответ: 0,15

14)При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 7°C. Найдите температуру вещества (в градусах Цельсия) через 6 минут после начала проведения опыта, если его начальная температура составляла −8°C .

Правильный ответ: -50

16)Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K . Другая прямая пересекает окружность в точках B и C, причём AB = 6 , BC = 48. Найдите длину отрезка AK .

Правильный ответ: 18

17)Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O , BC = 2, AD = 5 , AC = 28. Найдите длину отрезка AO .

Правильный ответ: 20

18)На клетчатой бумаге с размером клетки 1 1× изображён ромб. Найдите длину его большей диагонали.

Правильный ответ: 12

19)Какое из следующих утверждений верно? 1) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету. 2) Основания любой трапеции параллельны. 3) Всегда один из двух смежных углов острый, а другой тупой.

Правильный ответ: 2

21)Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 73 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72 % кислоты. Сколько процентов кислоты содержится в первом растворе?

Правильный ответ: 79

23)Найдите длину боковой стороны AB трапеции ABCD , если углы ABC и BCD равны 45° и 150° соответственно, а CD = 26 .

Правильный ответ: 13 корень из 2

24)Сторона BC параллелограмма ABCD вдвое больше стороны AB . Точка K — середина стороны BC. Докажите, что AK — биссектриса угла BAD .

25)Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 8 и MB =13. Касательная к окружности, описанной около треугольника ABC , проходит через точку C и пересекает прямую AB в точке D. Найдите длину отрезка CD .

Правильный ответ: 20,8

Сложные задания с 2 варианта:

1)Установите соответствие между стоимостями и номерами печей. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.

Правильный ответ: 321

2)Найдите площадь потолка парнóго отделения строящейся бани. Ответ дайте в квадратных метрах.

Правильный ответ: 7,7

3)Во сколько рублей обойдётся покупка дровяной печи, подходящей по объёму парного отделения, с доставкой, если доставка печи до дачного участка будет стоить 1400 рублей?

Правильный ответ: 20900

4)На дровяную печь, масса которой равна 48 кг, сделали скидку 10 %. Сколько рублей стала стоить печь без учёта доставки?

Правильный ответ: 17500

5)Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рис. 2. Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печи по дуге окружности с центром в середине нижней части кожуха (рис. 2). Для установки печи хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.

Правильный ответ: 65

10)В фирме такси в данный момент свободно 12 машин: 3 чёрные, 6 жёлтых и 3 зелёные. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.

Правильный ответ: 0,5

14)При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 6°C. Найдите температуру вещества (в градусах Цельсия) через 4 минуты после начала проведения опыта, если его начальная температура составляла −7°C .

Правильный ответ: -31

16)Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K . Другая прямая пересекает окружность в точках B и C, причём AB = 3, BC = 72. Найдите длину отрезка AK .

Правильный ответ: 15

17)Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O , BC =11, AD =15 , AC = 52 . Найдите длину отрезка AO .

Правильный ответ: 30

19)Какие из следующих утверждений верны? 1) В любой прямоугольной трапеции есть два равных угла. 2) Касательная к окружности параллельна радиусу, проведённому в точку касания. 3) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Правильный ответ: 13

21)Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 42 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40 % кислоты. Сколько процентов кислоты содержится во втором растворе?

Правильный ответ: 10

23)Найдите длину боковой стороны AB трапеции ABCD , если углы ABC и BCD равны 45° и 150° соответственно, а CD = 32.

Правильный ответ: 16 корень из 2

24)Сторона AB параллелограмма ABCD вдвое больше стороны AD . Точка L — середина стороны AB. Докажите, что DL — биссектриса угла ADC .

25)Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 4 и MB = 9 . Касательная к окружности, описанной около треугольника ABC , проходит через точку C и пересекает прямую AB в точке D . Найдите длину отрезка CD .

Видео:Факты про касающиеся окружности в задаче 16 #егэ2023 #математика #fyp #школа #математикапрофиль2023Скачать

На рисунке изображена прямая а касающаяся окружности

§ 20. Некоторые свойства окружности. Касательная к окружности

Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.

Если хорда является диаметром, то теорема очевидна.

На рисунке 287 изображена окружность с центром O , M — точка пересечения диаметра CD и хорды AB , CD ⊥ AB . Надо доказать, что AM = MB .

Проведём радиусы OA и OB . В равнобедренном треугольнике AOB ( OA = OB ) отрезок OM — высота, а значит, и медиана, т. е. AM = MB .

Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.

Докажите эту теорему самостоятельно. Подумайте, будет ли верным это утверждение, если хорда является диаметром.

На рисунке 288 показаны все возможные случаи взаимного расположения прямой и окружности. На рисунке 288, а они не имеют общих точек, на рисунке 288, б — имеют две общие точки, на рисунке 288, в — одну.

Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.

Касательная к окружности имеет только одну общую точку с кругом, ограниченным этой окружностью. На рисунке 288, в прямая a — касательная к кругу с центром в точке O , A — точка касания.

Если отрезок (луч) принадлежит касательной к окружности и имеет с этой окружностью общую точку, то говорят, что отрезок (луч) касается окружности. Например, на рисунке 289 изображён отрезок AB , который касается окружности в точке С .

Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

На рисунке 290 изображена окружность с центром O , A — точка касания прямой a и окружности. Надо доказать, что OA ⊥ a .

Предположим, что это не так, т. е. отрезок OA — наклонная к прямой a . Тогда из точки O опустим перпендикуляр OM на прямую a (рис. 291). Поскольку точка A — единственная общая точка прямой a и круга с центром O , то точка M не принадлежит этому кругу. Отсюда OM = MB + OB , где точка B — точка пересечения окружности и перпендикуляра OM . Отрезки OA и OB равны как радиусы окружности. Таким образом, OM > OA. Получили противоречие: перпендикуляр OM больше наклонной OA . Следовательно, OA ⊥ a .

(признак касательной к окружности)

Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведённому в эту точку, то эта прямая является касательной к данной окружности.

На рисунке 290 изображена окружность с центром в точке O , отрезок OA — её радиус, точка A принадлежит прямой a , OA ⊥ a . Докажем, что прямая a — касательная к окружности.

Пусть прямая a не является касательной, а имеет ещё одну общую точку B с окружностью (рис. 292). Тогда ∆ AOB — равнобедренный ( OA = OB как радиусы). Отсюда ∠ OBA = ∠ OAB = 90°. Получаем противоречие: в треугольнике AOB есть два прямых угла. Следовательно, прямая a является касательной к окружности.

Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.

Докажите это следствие самостоятельно.

Задача. Докажите, что если через данную точку к окружности проведены две касательные, то отрезки касательных, соединяющих данную точку с точками касания, равны.

Решение. На рисунке 293 изображена окружность с центром O . Прямые AB и AC — касательные, точки B и C — точки касания. Надо доказать, что AB = AC .

Проведём радиусы OB и OC в точки касания. По свойству касательной OB ⊥ AB и OC ⊥ AC . В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC .

507. Начертите окружность с центром O , проведите хорду AB . Пользуясь угольником, разделите эту хорду пополам.

508. Начертите окружность с центром O , проведите хорду CD . Пользуясь линейкой со шкалой, проведите диаметр, перпендикулярный хорде CD .

509. Начертите окружность, отметьте на ней точки A и B . Пользуясь линейкой и угольником, проведите прямые, которые касаются окружности в точках A и B .

510. Проведите прямую a и отметьте на ней точку M . Пользуясь угольником, линейкой и циркулем, проведите окружность радиуса 3 см, которая касается прямой a в точке M . Сколько таких окружностей можно провести?

511. На рисунке 294 точка O — центр окружности, диаметр CD перпендикулярен хорде AB . Докажите, что ∠ AOD = ∠ BOD .

512. Докажите, что равные хорды окружности равноудалены от её центра.

513. Докажите, что если хорды окружности равноудалены от её центра, то они равны.

514. Верно ли, что прямая, перпендикулярная радиусу окружности, касается этой окружности?

515. Прямая CD касается окружности с центром O в точке A , отрезок AB — хорда окружности, ∠ BAD = 35° (рис. 295). Найдите ∠ AOB .

516. Прямая CD касается окружности с центром O в точке A , отрезок AB — хорда окружности, ∠ AOB = 80° (см. рис. 295). Найдите ∠ BAC .

517. Дана окружность, диаметр которой равен 6 см. Прямая a удалена от её центра на: 1) 2 см; 2) 3 см; 3) 6 см. В каком случае прямая a является касательной к окружности?

518. В треугольнике ABC известно, что ∠ C = 90°. Докажите, что:

1) прямая BC является касательной к окружности с центром A , проходящей через точку C ;

2) прямая AB не является касательной к окружности с центром C , проходящей через точку A .

519. Докажите, что диаметр окружности больше любой хорды, отличной от диаметра.

520. В окружности с центром O через середину радиуса провели хорду AB , перпендикулярную ему. Докажите, что ∠ AOB = 120°.

521. Найдите угол между радиусами OA и OB окружности, если расстояние от центра O окружности до хорды AB в 2 раза меньше: 1) длины хорды AB ; 2) радиуса окружности.

522. В окружности провели диаметр AB и хорды AC и CD так, что AC = 12 см, ∠ BAC = 30°, AB ⊥ CD . Найдите длину хорды CD .

523. Через точку M к окружности с центром O провели касательные MA и MB , A и B — точки касания, ∠ OAB = 20°. Найдите ∠ AMB .

524. Через концы хорды AB , равной радиусу окружности, провели две касательные, пересекающиеся в точке C . Найдите ∠ ACB .

525. Через точку C окружности с центром O провели касательную к этой окружности, AB — диаметр окружности. Из точки A на касательную опущен перпендикуляр AD . Докажите, что луч AC — биссектриса угла BAD .

526. Прямая AC касается окружности с центром O в точке A (рис. 296). Докажите, что угол BAC в 2 раза меньше угла AOB .

527. Отрезки AB и BC — соответственно хорда и диаметр окружности, ∠ ABC = 30°. Через точку A провели касательную к окружности, пересекающую прямую BC в точке D . Докажите, что ∆ ABD — равнобедренный.

528. Известно, что диаметр AB делит хорду CD пополам, но не перпендикулярен ей. Докажите, что CD — также диаметр.

529. Найдите геометрическое место центров окружностей, которые касаются данной прямой в данной точке.

530. Найдите геометрическое место центров окружностей, которые касаются обеих сторон данного угла.

531. Найдите геометрическое место центров окружностей, которые касаются данной прямой.

532. Прямые, касающиеся окружности с центром O в точках A и B , пересекаются в точке K , ∠ AKB = 120°. Докажите, что AK + BK = OK .

533. Окружность касается стороны AB треугольника ABC в точке M и касается продолжения двух других сторон. Докажите, что сумма длин отрезков BC и BM равна половине периметра треугольника ABC .

534. Через точку C проведены касательные AC и BC к окружности, A и B — точки касания (рис. 297). На окружности взяли произвольную точку M , лежащую в одной полуплоскости с точкой C относительно прямой AB , и через неё провели касательную к окружности, пересекающую прямые AC и BC в точках D и E соответственно. Докажите, что периметр треугольника DEC не зависит от выбора точки M .

Упражнения для повторения

535. Докажите, что середина M отрезка, концы которого принадлежат двум параллельным прямым, является серединой любого отрезка, который проходит через точку M и концы которого принадлежат этим прямым.

536. Отрезки AB и CD лежат на одной прямой и имеют общую середину. Точку M выбрали так, что треугольник AMB — равнобедренный с основанием AB . Докажите, что ∆ CMD также является равнобедренным с основанием CD .

537. На стороне MK треугольника MPK отметили точки E и F так, что точка E лежит между точками M и F , ME = EP , PF = FK . Найдите угол M , если ∠ EPF = 92°, ∠ K = 26°.

538. В остроугольном треугольнике ABC проведена биссектриса BM , из точки M на сторону BC опущен перпендикуляр MK , ∠ ABM = ∠ KMC . Докажите, что треугольник ABC — равнобедренный.

Наблюдайте, рисуйте, конструируйте, фантазируйте

539. Установите закономерность форм фигур, изображённых на рисунке 298. Какую фигуру надо поставить следующей?

🎬 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

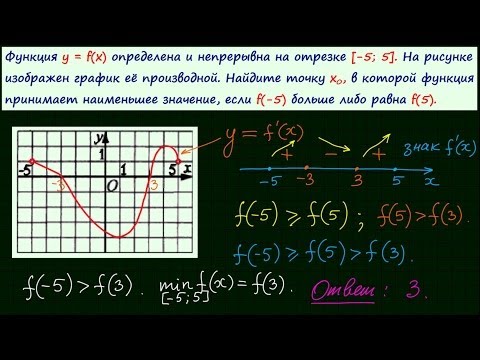
На рисунке изображён график функции y = f(x). Числа a, b, c, d и e задают на оси x четыре интервала.Скачать

Решаем все типы задач № 12Скачать

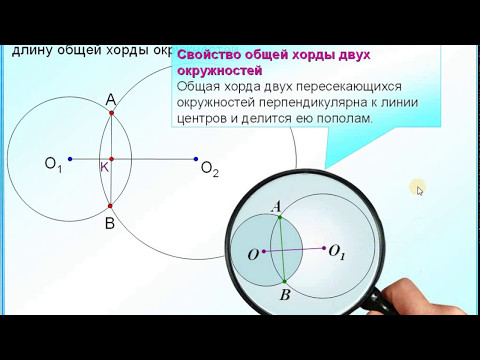
Задание 24 Две пересекающиеся окружностиСкачать

Задание № 4 из раздела Проверь себя - Геометрия 7 класс МерзлякСкачать

ОГЭ 2021 Ященко 7 вариант ФИПИ школе полный разбор!Скачать

ОГЭ по математике. Задание 16Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

КАСАЮЩИЕСЯ ОКРУЖНОСТИ. # ЕГЭ 2023Скачать

Егэ, c4, окружности вписаны в уголСкачать