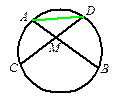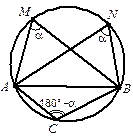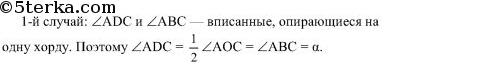О роли ключевых задач в системе учебников «Геометрия 7-9»
Задача 1. В треугольнике ABC известно, что ÐA = a. Биссектрисы углов B и C пересекаются в точке O. Докажите, что ÐBOC = 
.
1. Существует ли треугольник, две биссектрисы которого перпендикулярны?
2. Существует ли треугольник, в котором одна биссектриса делит пополам другую биссектрису?
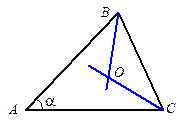
3. Биссектрисы BK и CM треугольника ABC пересекаются в точке O, ÐA = 60°. Докажите, что OK = OM.
4. Постройте треугольник АВС по углу А, стороне ВС и радиусу вписанной окружности.
5. В треугольнике АВС известны угол В и сторона АС. Найдите радиус окружности, описанной около треугольника АОС, где точка О — центр вписанной окружности треугольника АВС.
Задача 2. Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна её половине.
Задача 3. Медиана CM треугольника ABC равна половине стороны AB. Докажите, что треугольник ABC — прямоугольный.
1. Докажите, что любой треугольник можно разрезать на несколько равнобедренных треугольников.
2. В треугольнике ABC известно, что 
см, 
, 
. На стороне AC отметили точку D так, что 
см. Найдите углы треугольника BDC.
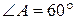
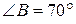
3. Высоты АЕ и ВF остроугольного треугольника АВС пересекаются в точке Н. Точки М и N — середины отрезков АВ и СН соответственно. Докажите, что МN ^ FE.
4. В прямоугольном треугольнике один из углов равен 15°. Докажите, что высота, проведённая к гипотенузе, в четыре раза меньше гипотенузы.
5. В треугольнике АВС сторона АС наибольшая. На продолжении стороны АС за точку С отметили точку D так, что СD = СВ. Докажите, что угол АВD не острый.
Указание. На стороне СА отметьте точку K так, что СK = СВ. Тогда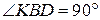 
.
Задача 4. Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяют по формуле 
, где r — радиус вписанной окружности, a и b — катеты, c — гипотенуза.
1.В прямоугольном треугольнике ABC отрезок CD — высота, проведённая к гипотенузе AB. Радиусы окружностей, вписанных в треугольники ACD, BCD и ABC, равны соответственно r1, r2 и r. Докажите, что r1 + r2 + r = CD.
2. Радиус окружности, вписанной в прямоугольный треугольник, равен полуразности катетов. Найдите острые углы треугольника.
3. Сумма радиусов вписанной и описанной окружностей прямоугольного треугольника равна одному из катетов. Найдите острые углы треугольника.
Задача 5. В треугольник ABC вписана окружность, касающаяся стороны AB в точке M, BC = a. Докажите, что AM = p – a, где p — полупериметр треугольника ABC.
1. В треугольнике ABC отрезок BD — медиана,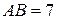 
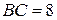
см, 
см. В треугольники ABD и BDC вписали окружности. Найдите расстояние между точками касания этих окружностей с отрезком BD.
2. В треугольнике АВС известно, что АВ = 5 см, ВС = 7 см, СА = 4 см. На стороне ВС отметили точку D так, что окружности, вписанные в треугольники АВD и АDС, касаются отрезка АD в одной точке. Найдите отрезок ВD.
3. Две вершины треугольника расположены в точках А и В, а третья вершина Х перемещается так, что разность ХА – ХВ = d, где d — заданное число. Докажите, что центры окружностей, вписанных в треугольники АХВ, принадлежат одной прямой.
Указание. Пусть окружность, вписанная в треугольник АХВ, касается отрезка АВ в точке K. Тогда АK =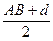 
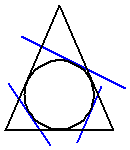
. Это означает, что центр вписанной окружности принадлежит прямой, перпендикулярной отрезку АВ и проходящей через точку K.
Задача 6. Через точку C проведены касательные AC и BC к окружности, A и B — точки касания. На окружности взяли произвольную точку M, лежащую в одной полуплоскости с точкой C относительно прямой AB, и через неё провели касательную к окружности, пересекающую прямые AC и BC в точках D и E соответственно. Докажите, что периметртреугольникаDEC не зависит от выбора точки M и равен 2AC.
1. В равнобедренный треугольник с основанием 12 см вписана окружность, а к ней проведены три касательные так, что они отсекают от данного треугольника три треугольника по одному возле каждой вершины. Сумма периметров трёх образовавшихся треугольников равна 48 см. Найдите боковую сторону данного треугольника.
2. В треугольник со сторонами 6 см, 10 см, 12 см вписана окружность. К окружности проведена касательная так, что она пересекает две бóльшие стороны треугольника. Найдите периметр треугольника, который касательная отсекает от данного треугольника.
3. Через данную точку проведите прямую, отсекающую от данного угла треугольник данного периметра.
Задача 7. Докажите, что биссектрисы двух внешних углов с вершинами A и C треугольника ABC и биссектриса угла В пересекаются в одной точке, причём ÐAOC = 
.
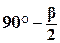
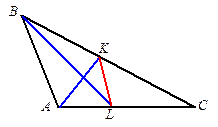
2. В треугольнике ABC проведены биссектрисы AK и BL. Найдите угол A, если луч KL — биссектриса угла AKC.
3. В треугольнике АВС провели биссектрису АЕ. На стороне АС отметили точку D так, что 
Докажите, что луч DЕ — биссектриса угла ВDС.
Указание.Докажите, что луч ВС — биссектриса внешнего угла треугольника АВD.
4.На сторонах BC и CD квадрата ABCD отметили соответственно точки M и N так, что ÐMNC = 2ÐNAD. Найдите величину угла MAN.
Задача 8. Хорды AB и CD окружности пересекаются в точке M. Докажите, что ÐAMC = 
(ÈAC + ÈBD).
Задача 9. Хорды AB и CD окружности не пересекаются, а лучи AB и CD пересекаются в точке M). Докажите, что ÐAMC = (ÈAC – ÈBD).
1. На окружности отметили четыре точки. Середины образовавшихся дуг соединили отрезками, как показано на рисунке. Докажите, что проведённые отрезки перпендикулярны.
2. Дан отрезок AB. Найдите геометрическое место точек X таких, что треугольник AXB: 1) прямоугольный; 2) остроугольный; 3) тупоугольный.
3. В четырёхугольнике три тупых угла. Докажите, что из двух его диагоналей больше та, которая проведена из вершины острого угла.
Задача 10. Точки O и C расположены в одной полуплоскости относительно прямой AB. Известно, что OA = OB и ÐAOB = 2ÐACB. Докажите, что точки A, B и C лежат на окружности с центром в точке O.
Задача 11. Точки O и C расположены в разных полуплоскостях относительно прямой AB. Известно, что AO = OB и ÐAOB = 2(180° – ÐACB). Докажите, что точки A, B и C лежат на окружности с центром в точке O.
1. В выпуклом четырёхугольнике ABCD известно, что ÐBAD = 100°, ÐBCD = 130°, AB = AD. Докажите, что AB = AC.
2. Дан квадрат ABCD. Вне квадрата отметили точку E так, что ÐBAE = 30°, ÐBCE = 75°. Найдите ÐCBE.
3. В треугольнике ABC известно, что ÐC = 10°, ÐB = 20°. Вне треугольника отметили точку M так, что треугольник CMB — равносторонний, точки M и A лежат в разных полуплоскостях относительно прямой BC. Найдите углы MAB и MAC.
4. Даны равнобедренный треугольник ABC (AB = AC) и точка M, ему не принадлежащая, но принадлежащая углу ABC. Найдите ÐBAM, если ÐABC = 50°, ÐBMC = 40°, ÐBMA = 10°.
5. В треугольнике ABC известно, что ÐBAC = 30°, ÐABC = 80°. В треугольнике отметили такую точку K, что треугольник BCK — равносторонний. Найдите ÐKAB.
6. В трапеции ABCD (AD || BC) угол ADB в 2 раза меньше угла ACB, BC = AC = 5 см. Найдите сторону CD.
Задача 12. (признак принадлежности четырёх точек одной окружности). Точки A, M, N, B таковы, что ÐAMB = ÐANB, причём точки M и N лежат в одной полуплоскости относительно прямой AB. Докажите, что точки A, M, N, B лежат на одной окружности.
1.На сторонах BC и CD квадрата ABCD отмечены точки M и N так, что ÐMAN = 45°. С помощью только линейки опустите перпендикуляр из точки A на прямую MN.
2. Из точки M, принадлежащей углу АОВ, но не принадлежащей его сторонам, опущены перпендикуляры MM1 и MM2 на прямые OA и OB. Докажите, что M1M2 £ OM.
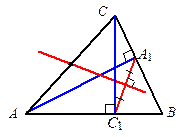
3. В остроугольном треугольнике ABC отрезки CC1 и AA1 — высоты. Докажите, что серединный перпендикуляр отрезка C1A1 проходит через середину стороны AC.
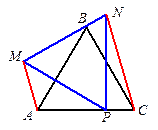
4. Равносторонние треугольники ABC и MNP расположены так, что вершина B лежит на стороне MN, а вершина P — на стороне AC. Докажите, что AM || NC.
5. На медиане BM треугольника ABC отметили точку K так, что ÐMKC = ÐBCM. Докажите, что ÐAKM = ÐBAM.
Видео:На окружности отмечены точки А и В так, что меньшая дуга АВ равна 68°. Прямая ВС касается окружностиСкачать
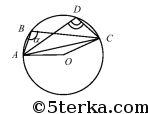
№ 54. На окружности отмечены четыре точки А, В, С, D.
Чему равен угол ADC, если угол АВС равен а? (Два случая.)
2-й случай: в ΔАОС ∠АОС = 360° — 2а, так как дополнительный к нему угол ∠АОС = 2а, как центральный угол, соответствующий описанному ∠В = а.
∠ADC = 1/2 ∠АОС = 2 (360° — 2а) = 180° — а. Ответ: 1) а; 2) 180° — а.
Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №54
к главе «§11. Подобие фигур».
Видео:2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать
На окружности отмечены 4 точки середины
Ответ:
Объяснение:
CZ⊥GC, значит GZ — диаметр. (Вписанный угол, опирающийся на диаметр, — прямой)
По условию CK=GZ, значит СК — тоже диаметр.
Значит вписанные углы CGKZ — прямоугольник.
📹 Видео
На окружности отмечены точки A и B так, что меньшая дуга AB равна 92 градуса. Прямая BC касается окрСкачать
Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать
ОГЭ по математике. На окружности отмечены точки. (Вар. 2) √17 модель геометрия ОГЭСкачать
ОГЭ ЗАДАНИЕ 16 НА ОКРУЖНОСТИ ОТМЕЧЕНЫ ТОЧКИ А И В НАЙДИТЕ ДЛИНУ БОЛЬШЕЙ ДУГИ ЕСЛИ МЕНЬШАЯ 58Скачать
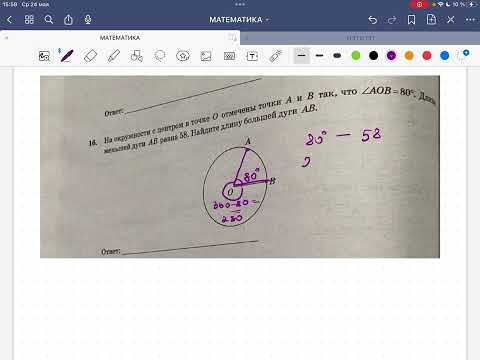
На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
ОГЭ по математике. На окружности отмечены точки. (Вар. 1) √ 17. Модель геометрияСкачать
Задание 16 из ОГЭ. Найдите длину большей дуги.Скачать
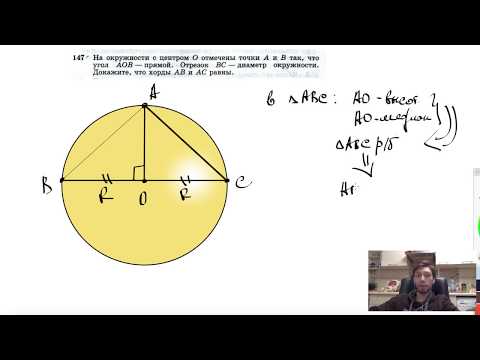
№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать
На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
10 класс, 11 урок, Числовая окружностьСкачать
ОГЭ по математике. На окружности отмечены точки (вар. 3) √ 17 модель геометрия ОГЭСкачать
В треугольнике отмечены середины M и N сторон BC и AC ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать
ОГЭ 2020 Задание 17Скачать
ОГЭ по математике. На окружности отмечены точки. Вар. 3 (17)Скачать
Решение задач на окружность явную и вспомогательнуюСкачать
Задачи региона ВсОШ на степень точкиСкачать
Найдите расстояние от точки A до середины отрезка BC. ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
